Quantitative Method 2
R2:Organizing, Visualizing, and Describing Data
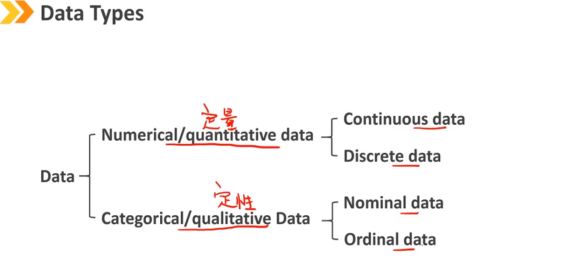
Ⅰ、Data Types:数据类型


两个基本概念:
变量是一种可以测量、计数或分类的特征或数量,可以变化。变量也可以称为字段、属性或特征
例如:股价
观察值是在某个时间点或指定时间段内收集的特定变量的值
例如:某一个时刻的股价


数字数据 数字数据是将测量或计数的数量表示为数字的值,也称为定量数据。 连续数据:可以测量的数据,可以在指定的值范围内采用任何数值 例如:股票的收益率 离散数据:计数过程中产生的可数数值 例如:股票报价以0.01元为单位,¥3.50、¥3.51、¥3.52


分类数据 也称为定性数据,可以用作标签,将数据集划分为多个组以进行汇总和可视化。 分类数据:不能排序的分类值。 例如:小盘股/中盘股/大盘股 有序数据:可以逻辑排序的分类值。 类别不一定确定每个类别之间的数字差异 例如:五星/四星/三星






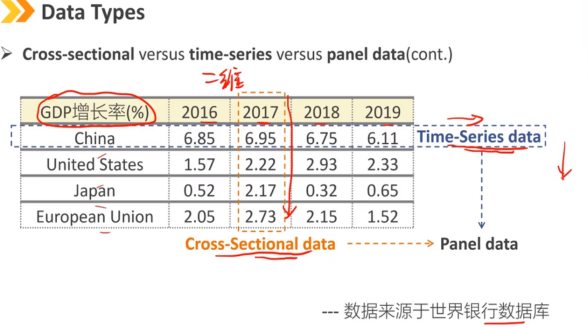
横截面数据、时间序列数据和面板数据
横截面数据是多个观测单元在给定时间点的观测结果列表。
时间序列数据是单个观测单元的一系列观测数据,这些观测数据以离散且通常等间距的时间间隔收集,例如每天、每周、每月、每年。
面板数据是财务分析和建模中经常使用的时间序列和横截面数据的组合。


结构化数据与非结构化数据 结构化数据以预定义的方式进行高度组织,相对容易输入、存储、查询和分析,无需太多手动处理 (可以被Excel函数/透视表直接处理的数据) 一维数组 二维数据表


结构化数据与非结构化数据(续)
相反,非结构化数据是不遵循任何常规组织形式的数据。
例如:文本、图像、视频、音频
通过社交媒体帖子、公司监管文件、卫星图像等制作
必须首先将非结构化数据转换为模型可以处理的结构化数据


Ⅱ、Organizing Data for Quantitative Analysis:数据的整理和归纳


一维数组:时间序列或横截面数据
例如:ABC股份有限公司股票上市后前10个交易日的收盘价。
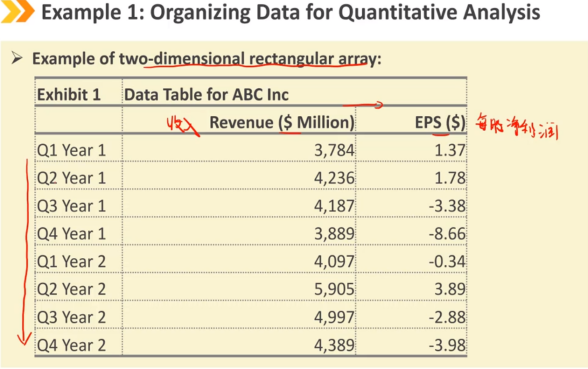
二维矩阵:
与Excel电子表格中的结构类似,数据表由列和行组成,分别保存多个变量和多个观察值。
列 → 不同的变量
行 → 每个变量的观测值
均可升序或降序
Ⅲ、Summarizing Data Using Frequency Distributions:用频率分布对数据进行归纳(定量数据)


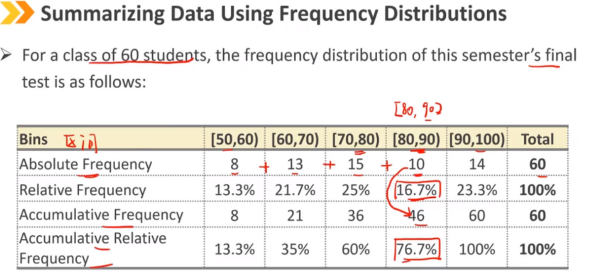
频率分布是构建数据的表格显示:
通过按不同的值或组计算变量的观察值;
通过将一个数值变量的值计数到一组数字有序的区间中。
区间不能重叠
区间宽度既不能太大也不能太小


绝对频率,或简单的原始频率,是每个值或每个区间内计算的观察值的实际个数 相对频率 = 绝对频率 / 观察总数 当我们从第一个区间移动到最后一个区间时,累积频率会累积求和观测值 累积绝对频率 / 累积相对频率 某个区间的累积频率是小于或等于该区间上限的观察值个数 最后一个区间的累积频率为总个数,或100%(累积相对频率)
Ⅳ、Summarizing Data Using a Contingency Table:用相关性表格对数据进行归纳(定性数据)


列联表是一种表格格式,显示两个或多个分类变量的频率分布,用于查找变量之间的模式。
双向表:两个分类变量的列联表。
联合频率:将行中的一个变量与列中的另一个变量连接起来,以计算观测值数量。
然后跨行和跨列添加联合频率,这些对应的总和称为边际频率。
边际频率表示每个变量的频率分布。


列联表也以百分比表示频率为相对频率;
我们可以将联合频率除以:
总数
行上的边际频率
列上的边际频率

Ⅴ、Data Visualization:数据可视化


可视化是以图形或图表格式表示数据,以提高对数据的理解。
“一幅画胜过千言万语。”
在本部分中,我们将介绍几种可视化方法,包括:
柱状图和频率多边形
条形图
树形图
词云
折线图
散点图
热力图
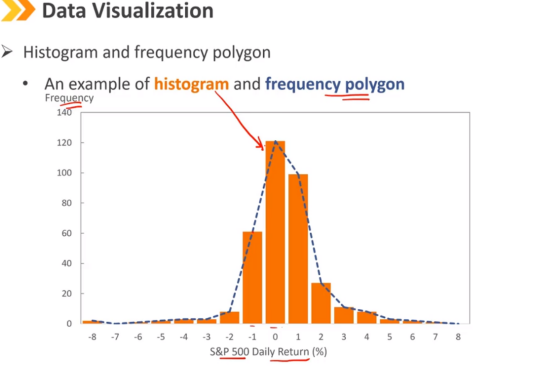
1、Histogram and frequency polygon


柱状图和频率多边形
柱状图是一种图表,通过使用条形或列的高度表示分布中每个区间的频率来表示数字数据的分布。
y轴:绝对频率或相对频率
x轴:变量的区间
频率多边形:我们在x轴上绘制每个区间的中点,并在y轴上绘制该区间的频率,然后我们用一条直线连接相邻的各点。


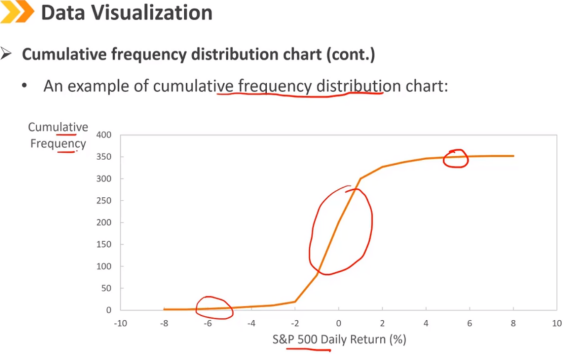
累计频率分布图:
坐标轴的含义:
y轴:累积绝对频率或累积相对频率
x轴:区间的上限
显示低于某个值的观察值的数量或百分比
2、Bar chart


条形图
分类数据的频率分布可以绘制在类似的条形图中。在条形图中,每个条形图表示一个不同的类别,而不是一个区间。
垂直条形图
y轴:频率
x轴:类别
水平条形图
y轴:类别
x轴:频率



条形图(续)
对于两个分类变量,我们需要一个增强版的条形图,称为分组条形图(也称为群集条形图),以显示联合频率。
对于水平分组条形图:
y轴:分类变量在同一部门内并排聚集
x轴:频率
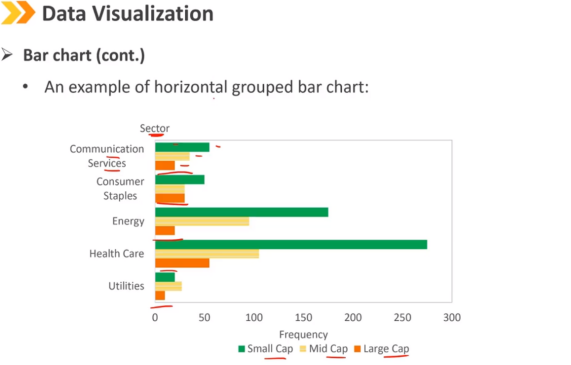


条形图(续)
呈现两个分类变量联合频率分布的另一种形式是堆积条形图。
在堆积条形图的垂直版本中:
代表子组的条相互重叠,形成一个条;
条形图的每个小节以不同的颜色显示,以表示对每个子组的贡献;
总高度:该类别的边际频率
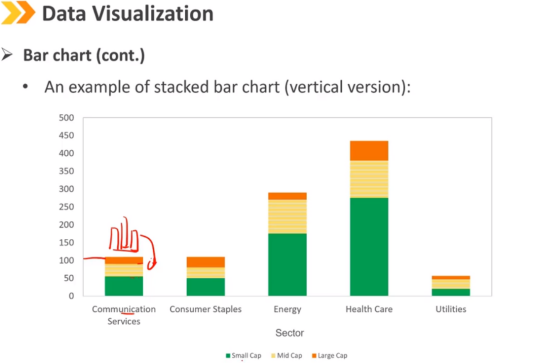


条形图(续)
在特定情况下,条形图中的类别按频率降序排列,并且条形图包含一条显示累计相对频率的线,则称为帕累托图。
该图表通常用于突出显示主要类别或最重要的组。
3、Tree-map


树形图
树形图是另一种显示分类数据的图形工具。
它由一组表示不同组的彩色矩形组成,每个矩形的面积与相应组的值成比例。
树形图可以通过显示一组嵌套的矩形来表示具有其他维度的数据。
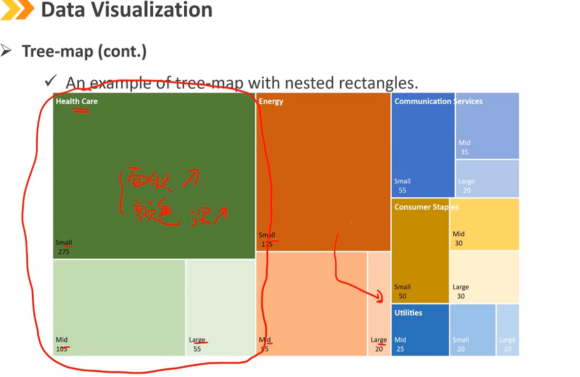
4、Word cloud


词云
词云是表示文本数据的可视化设备。
每个不同单词的大小与它在给定文本中出现的频率成正比。
快速感知最常用的术语
表达不同情感的词语可能会以不同的颜色显示出来

5、Line chart


折线图
折线图是一种用于可视化有序观测的图形。
通常使用折线图来显示数据系列随时间的变化。
折线图以清晰简洁的方式显示数据的变化和基本趋势。
可以进行多行比较。
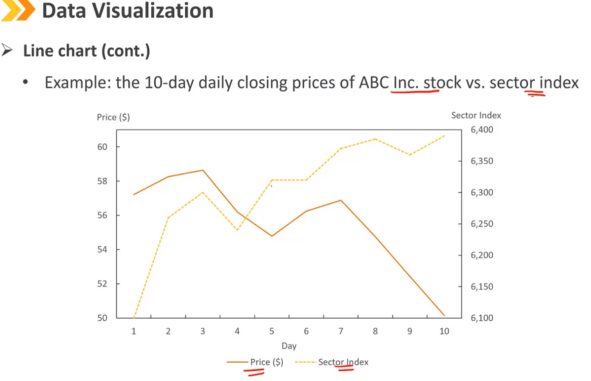
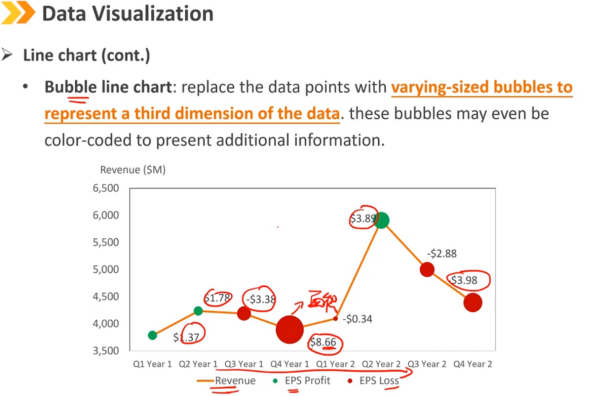

折线图(续)
气泡折线图:用大小不同的气泡替换数据点,以表示数据的第三维,这些气泡甚至可以进行颜色编码以显示其他信息。
6、Scatter plot


散点图
散点图是一种图形,用于显示两个数值变量的内部变化。
x轴:一个变量
y轴:另一个变量
点:特定时间点的两个变量的值
散点图传达了大量有价值的信息:
检查是否存在任何潜在关联
发现极值
快速感知数据范围
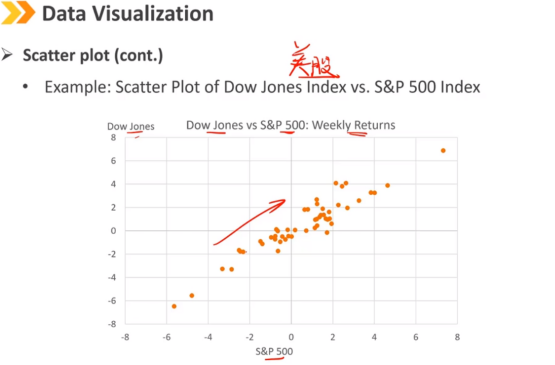
7、Heat Map
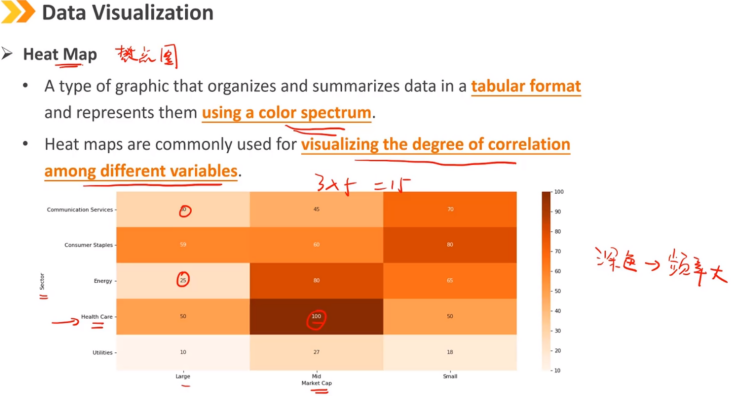

热力图
一种图形,以表格格式组织和汇总数据,并使用光谱表示数据。
热力图通常用于显示不同变量之间的关联程度。


分析师应避免的四个典型陷阱:
选择了不正确的图表类型来显示数据
有选择地绘制数据,以支持分析师打算得出的结论
数据在y轴不从零开始的被删减的图中绘制是不适当的
坐标轴的缩放不当
Ⅵ、Measures of Central Tendency:数据集中趋势的测量


统计量是对一组观察结果的汇总度量。
如果统计量汇总了一个总体的所有可能观察值集,我们将统计量称为参数。
如果统计数据汇总了作为总体子集(样本)的一组观察数据,我们将该统计数据称为样本统计数据。


中心趋势度量是使用最广泛的统计度量,因为它们可以很容易地计算和应用。


算术平均值
算术平均值是观测值之和除以观测值数量。
平均值周围的偏差等于0。
算术平均值对极值敏感。



加权平均数
算术平均数确实是加权平均数之一,其中所有权重相等




几何平均数:
几何平均数最常用于计算随时间变化的平均收益率或变量的增长率。


计算多年投资的平均年收益率时,使用几何平均数。



调和平均数
调和平均数适用于比率的变量。
XH的倒数,是Xi倒数的算术平均值
调和平均数可视为一种特殊类型的加权平均数,其权重与其大小成反比。
在存在异常值的情况下,调和平均数作为集中趋势的度量非常有用。
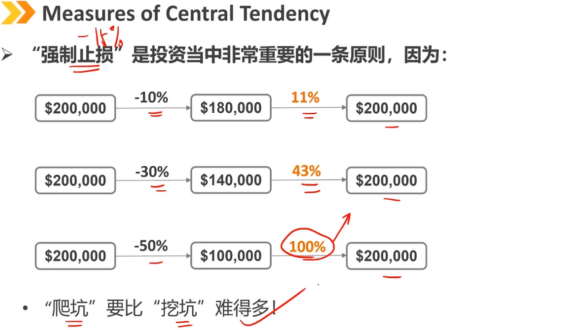
调和平均数在投资策略中的一个著名应用是成本平均法:固定金额的定期投资。

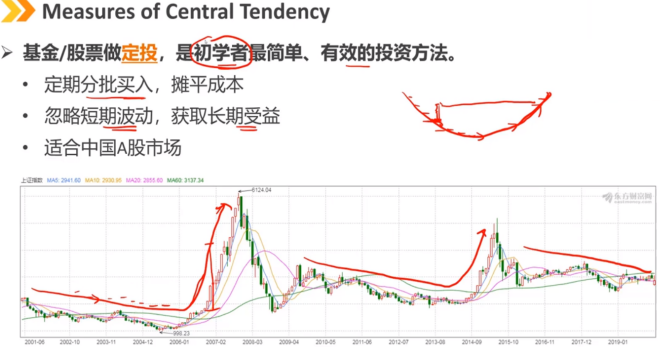

注:数据分布越离散(方差越大),算数平均数和几何平均数之间的差值越大(A-G越大)

在财务分析中使用不同的方法: 算术平均数通常用于预测未来的业绩表现 几何平均数通常用于说明过去的业绩表现,尤其是复合收益率/增长率 调和平均数通常用于每次投资固定金额的定期投资 数学上相互关联:A×H = G^2 只要观察值不都相等(方差≠0)且为正,我们就有:A > G > H


中位数 中位数是按升序排序的一组数据中间项的值。 在奇数样本中,中位数是占据第 (n+1)/2 位置的数 {2,5,7,11,14} → 中位数=7 在偶数样本中,我们将中位数定义为占据 n/2 和 (n+2)/2 位置的数据的平均值 {3,9,10,20} → 中位数=(9+10)/2=9.5 与平均数不同,中位数不受极值的影响。


众数 众数是数据集中出现次数最多的值 {2,4,5,5,7,8,8,8,10,12} → 众数=8 一个数据集可以有多个众数,甚至没有众数 众数区间:频率最高的数据区间 众数是唯一可用于分类数据的集中趋势测量指标
Ⅶ、Quantiles:分位数


分位数用于描述升序数据中的观测位置。
分位数是表示某个值的最通用术语,该值等于或低于某一规定分隔位置的数据。
常用分位数包括:
四分位数
五分位数
十分位数
百分位数


第y百分位数表示 y% 的数据位于其下方,而 (1-y)% 的数据位于其上方 最常用的是百分位数,可以根据它们定义其他度量 第一四分位数(Q1)是第25个百分位数 第三四分位数(Q3)是第75个百分位数 四分位数范围(IQR)是第三四分位数和第一四分位数之间的差值,即 IQR = Q3 - Q1


近似计算第y百分位数的方法
在数据量很少,计算位置很偏的情况下,该方法会失真,不能使用。
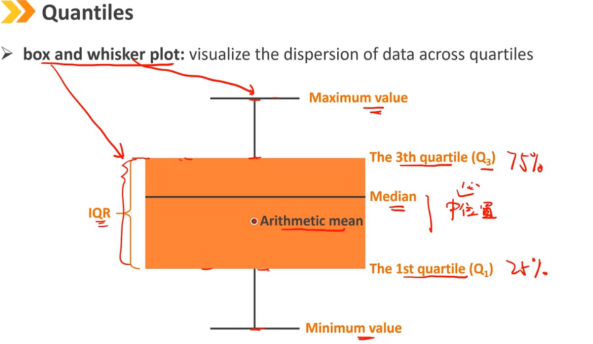

箱线图:可视化数据在四分位数之间的离散度


投资实践中的分位数
投资组合绩效评估
投资经理的绩效通常以其相对于同行绩效下降的分位数为特征。
如果投资经理的业绩超过同行的90%(前10%),他将获得更高的奖金


投资实践中的分位数(续)
投资策略制定与研究
在投资研究中,分析师总是根据某些特征(规模、流动性、市盈率、交易量等)将数据分为若干个分位数,并评估该特征的影响。
比较25%的最小规模股票和25%的最大规模股票的收益率
Ⅷ、Measures of Dispersion:数据离散程度的测量


离散度是围绕中心趋势的变化。在投资中,如果平均收益衡量的是报酬问题,那么离散度衡量的是风险问题。


范围
范围是数据集中最大值和最小值之间的差值。
平均绝对偏差(MAD)
MAD是数据集中与平均值的平均绝对距离。
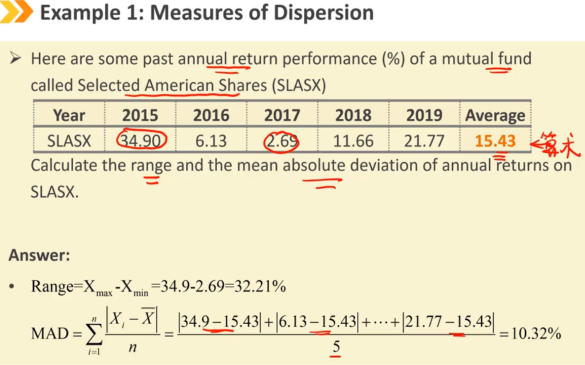


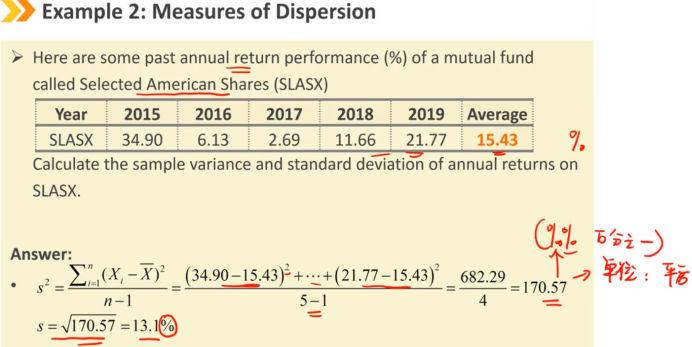
方差是距离均值偏差的平方的平均值


标准差是方差的正平方根
标准差使用与原始数据和算术平均值相同的单位
在许多定价模型中,波动率是通过标准差来衡量的
Ⅸ、Downside Deviation and Coefficient of Variation:下半标准差和变异系数


目标下半标准差,也称为目标半标准差,是对低于目标值的观测值离散程度的衡量。
对于投资而言,下半标准差衡量的是意外损失的风险。
B是目标值
n是样本观察的总数


变异系数(CV)是一组观测值的标准差与其平均值的比率
当观察结果是收益时,变异系数衡量每单位收益的风险量
平均值必须为正
变异系数没有测量单位

Ⅹ、The Shape of the Distributions:数据分布的形状


偏度衡量分布缺乏对称性的程度。 不对称的分布是倾斜的。 在对称分布中,偏度=0,平均值=中位数=众数。 偏度是数据的三阶指标,没有单位。


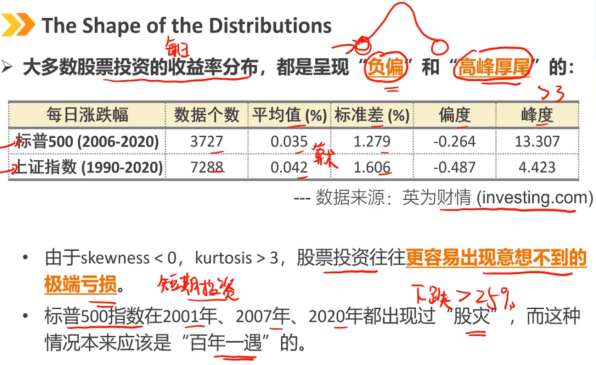
正偏分布的偏度 > 0 正偏 = 右偏 正偏的收益率分布经常出现小幅亏损和少数极端收益,因此投资者更喜欢正偏的收益率 在正偏分布中,平均值 > 中位数 > 众数
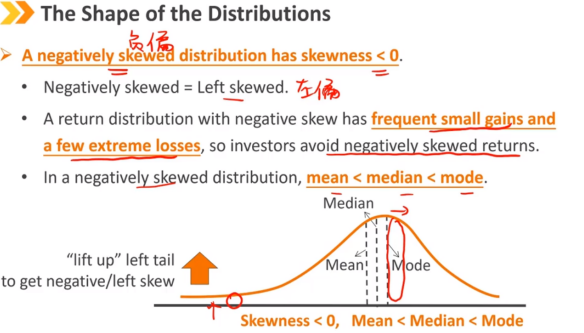

负偏分布的偏度 < 0 负偏 = 左偏 负偏的收益率分布经常会有小幅度的收益和一些极端的损失,因此投资者会避免负偏的收益率 在负偏分布中,平均值 < 中位数 < 众数


峰度 峰度是尾部分布相对于其余分布的组合权重的度量。 正态分布的峰度 = 3(称为中峰度) 就尾部相对权重而言,类似于正态分布的分布被称为中峰度。
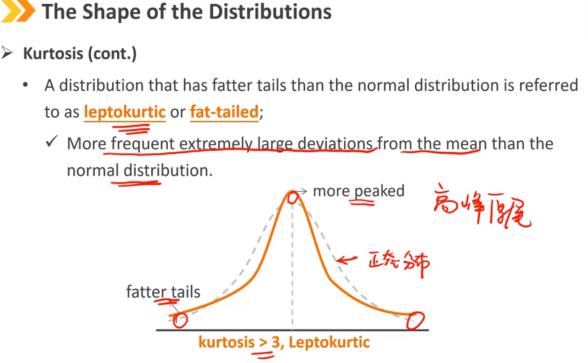

峰度(续) 具有比正态分布更厚尾巴的分布称为厚尾分布。(峰度 > 3) 与正态分布相比,与平均值的偏差更大,极端值出现的概率更大
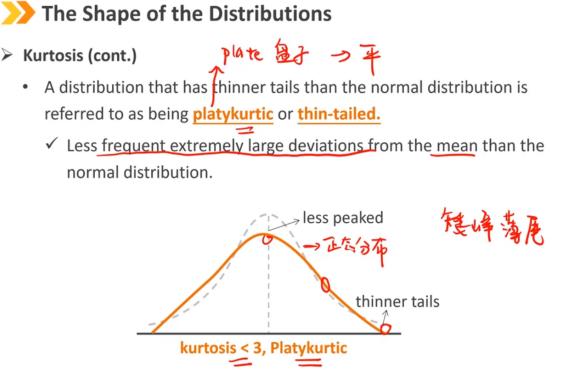

峰度(续) 尾巴比正态分布细的分布称为细尾分布。(峰度 < 3) 与正态分布相比,与平均值的偏差更小,极端值出现的概率更小


excess kurtosis = 峰度 - 3 没有单位
Ⅺ、Correlation between Two Variables:相关系数

样本协方差是样本中两个变量如何一起移动的度量。
协方差是两个随机变量联合变化性的度量。
如果随机变量沿相同(相反)方向变化,则其协方差为正(负)。


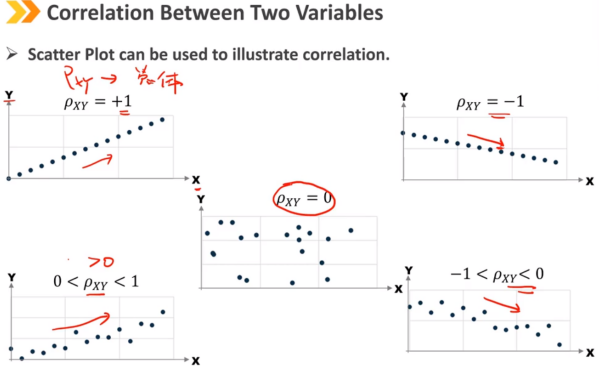
样本相关系数是样本中两个变量如何一起移动的标准化度量。(剔除变量自己的波动性) 相关系数表示两个随机变量之间线性关系的强度。 相关系数没有单位。 相关系数范围为-1和+1。 相关系数=0表示变量之间不存在线性(直线)关系(不相关 ≠ 独立) 正(负)相关性的增加表明正(负)线性关系越来越强。

Summary:












 浙公网安备 33010602011771号
浙公网安备 33010602011771号