可持久化线段树

可持久化权值线段树

· 又叫主席树

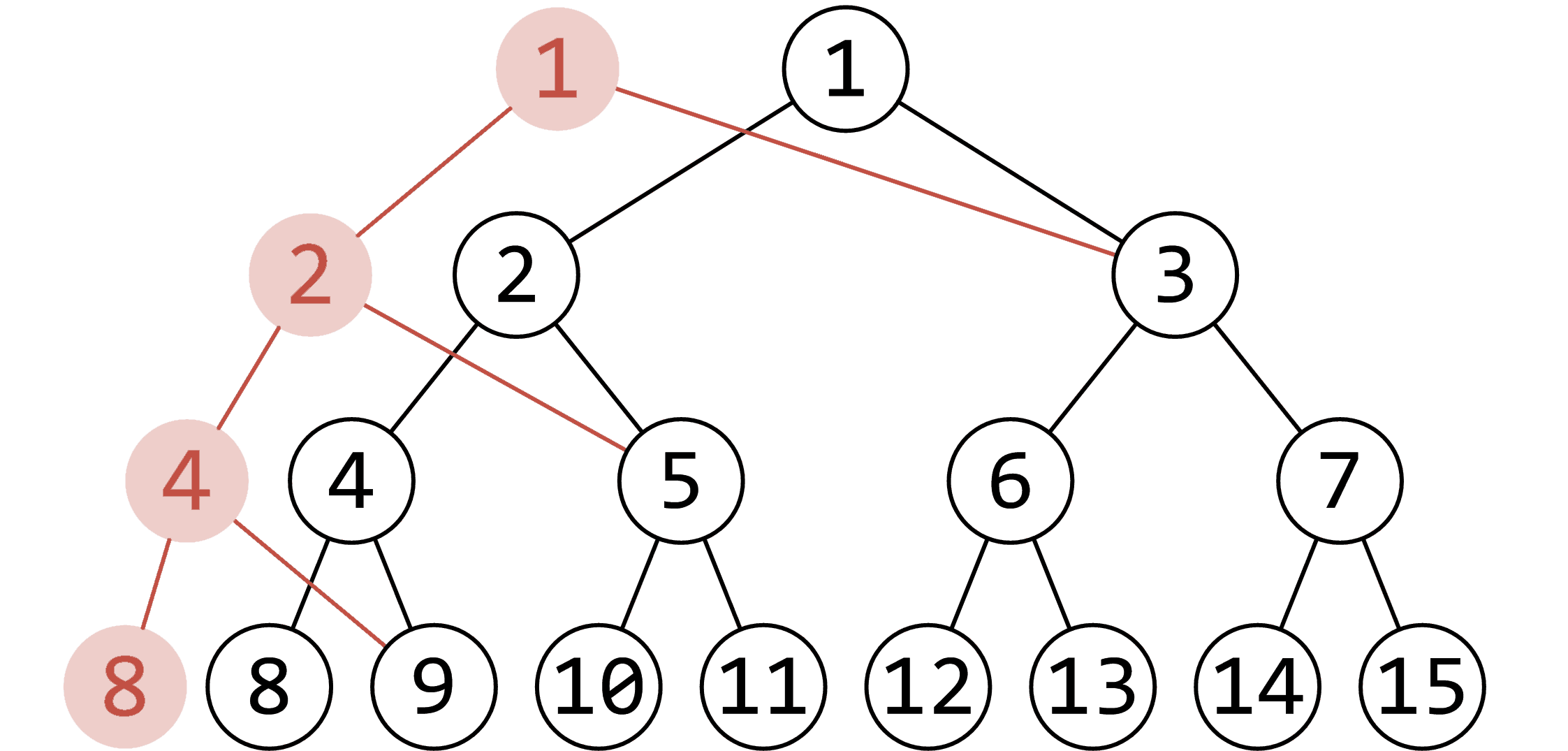
· 本质就是多棵线段树

· 可持久化表示可以维护历史任一版本的数据

· 例题

\(\quad\) · Q1：给定 \(n\) 个整数构成的序列 ，需要支持两种操作

\(\quad\quad\) · 在某个历史版本上修改某一个位置上的值

\(\quad\quad\) · 访问某个历史版本上的某一位置的值

\(\quad\) · A1: 保存每次插入操作时的历史版本.

\(\quad\quad\) · 对于每次操作都开一棵线段树

\(\quad\quad\) · 空间显然会爆，考虑优化

\(\quad\quad\) · 可以观察到，对于每次修改操作，最多更改 \(O(\log n)\) 个节点（单点修改最多遍历 \(O(\log n)\) 个节点）

\(\quad\quad\) · 因此对于每次修改，动态开点记录修改的状态。这样可以大大地减少冗余

\(\quad\quad\) · 注意存树一定要动态开点！！！

\(\quad\) · Code:

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iostream>

using namespace std;

const int kmax = 1e6 + 3;

int n, m, a[kmax];
int rt[kmax];

struct Segment {
  struct Tree {
    int l, r, mid, s;
    int ls, rs;     //记录左右儿子
  } t[kmax << 5];
  int tc;

  Segment() {
    tc = 0;
  }

  int Build(int x, int l, int r) {
    t[x] = {l, r, (l + r) >> 1};
    if (l == r) {
      t[x].s = a[l];
      return x;
    }
    t[x].s = 0;
    t[x].ls = Build(++tc, l, t[x].mid);    //动态开点储存节点
    t[x].rs = Build(++tc, t[x].mid + 1, r);
    return x;
  }

  int Modify(int x, int k, int v) {
    t[++tc] = t[x];     //记录新版本
    x = tc;
    if (t[x].l == k && k == t[x].r) {
      t[x].s = v;
      return x;
    }
    if (k <= t[x].mid) {
      t[x].ls = Modify(t[x].ls, k, v);
    } else {
      t[x].rs = Modify(t[x].rs, k, v);
    }
    return x;
  }

  int Query(int x, int k) {
    if (t[x].l == t[x].r && t[x].l == k) {
      return t[x].s;
    }
    if (k <= t[x].mid) return Query(t[x].ls, k);
    return Query(t[x].rs, k);
  }

} tr;

int main() {
  scanf("%d%d", &n, &m);
  for (int i = 1; i <= n; i++) {
    scanf("%d", &a[i]);
  }
  rt[0] = tr.Build(++tr.tc, 1, n);
  for (int i = 1, tim, op, x, v; i <= m; i++) {
    scanf("%d%d%d", &tim, &op, &x);
    if (op == 1) {
      scanf("%d", &v);
      rt[i] = tr.Modify(rt[tim], x, v);
    } else {
      printf("%d\n", tr.Query(rt[tim], x));
      rt[i] = rt[tim];
    }
  }
  return 0;
}

\(\quad\) · Q2：给定 \(n\) 个整数构成的序列 ，将对于指定的闭区间 \([l,r]\) 查询其区间内的第 \(k\) 小值。

\(\quad\) · A2: 简化问题，求 \([1,p]\) 的第 \(k\) 小值。

\(\quad\quad\) · 对于简化问题，只需要找到插入 \(p\) 时的根节点版本，然后在普通权值线段树进行操作就行了

\(\quad\quad\) · 联系到 前缀和,只需要用 \([1, r]\) 的结果减去 \([1, l-1]\) 的结果就行了。（显然主席树统计满足区间减法的性质）

\(\quad\) · Code:

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iostream>

using namespace std;

const int kmax = 2e5 + 3;

struct Segment {
  int s;
  int ls, rs;
} t[kmax << 5];

int n, m, c, p, tc;
int a[kmax], b[kmax];
int rt[kmax];

void Build(int &x, int l, int r) {
  x = ++tc;
  if (l == r) return;
  int mid = (l + r) >> 1;
  Build(t[x].ls, l, mid);
  Build(t[x].rs, mid + 1, r);
}

int Modify(int x, int l, int r, int k) {
  int _x = ++tc;
  t[_x] = t[x];
  t[_x].s = t[x].s + 1;
  if (l == r) return _x;
  int mid = (l + r) >> 1;
  if (k <= mid) {
    t[_x].ls = Modify(t[_x].ls, l, mid, k);
  } else {
    t[_x].rs = Modify(t[_x].rs, mid + 1, r, k);
  }
  return _x;
}

int Query(int x, int y, int l, int r, int k) {
  if (l == r) return l;
  int d = t[t[y].ls].s - t[t[x].ls].s;
  int mid = (l + r) >> 1;
  if (d >= k) return Query(t[x].ls, t[y].ls, l, mid, k);
  return Query(t[x].rs, t[y].rs, mid + 1, r, k - d);
}

int main() {
  scanf("%d%d", &n, &m);
  for (int i = 1; i <= n; i++) {
    scanf("%d", &a[i]);
    b[i] = a[i];
  }
  sort(b + 1, b + n + 1);
  c = unique(b + 1, b + n + 1) - b - 1;
  Build(rt[0], 1, c);
  for (int i = 1; i <= n; i++) {
    p = lower_bound(b + 1, b + c + 1, a[i]) - b;
    rt[i] = Modify(rt[i - 1], 1, c, p);
  }
  for (int i = 1, l, r, k; i <= m; i++) {
    scanf("%d%d%d", &l, &r, &k);
    printf("%d\n", b[Query(rt[l - 1], rt[r], 1, c, k)]);
  }
  return 0;
}