残差之美——ESKF与ResNet

残差是什么？一言以蔽之，真实值与估计值之间的误差。

在状态估计与非线性优化中，残差这个概念被广泛运用。无论是滤波器中计算新息与状态更新，还是优化器里的损失函数，都要用到残差这个概念。深度学习中也有残差的概念。最近在梳理自己的笔记时，意外发现ResNet和ESKF都用到了了残差易于优化的性质，从而达到更好优化的目的，特此记录。

ESKF

在我之前写的一篇文章[1]中已经提到，相比于直接估计状态，估计状态与真实值之间的残差，其线性化程度更好，那么协方差在传递的时候，更能反映状态的不确定性，刻画的更准确。此外，考虑到SO3旋转的特性，估计残差不容易遇到状态值发生万向节死锁的问题。

ResNet

ResNet是Kaiming HE在CVPR 2016发的一篇论文。彼时，深度学习还处在堆CNN层数的年代。其实没人能说明，对于一个具体任务，其卷积层的数量究竟该是多少。但大部分人都有一个朴素的愿望，认为卷积层层数更多的模型，至少其模型性能应当大于等于层数更少的模型。然而事实上，即使加了BN层以防止梯度消失或者梯度爆炸，当卷积层数量堆上去后，性能却不如那些小模型。为什么呢？

Kaiming认为，如果一个模型的深度是对一个任务是足够用的，比如一个100层的模型，只用其前70层的卷积层就足以把分类问题刻画的很好了，那么后30层理论上就没有残差或者残差很小，输出x=f(x)的恒等映射就行了。问题在于，目前的CNN层能很好的刻画或者学习恒等映射么？

回顾一下卷积层输出结果的公式：

\[y = Relu(w*x) \]

想使得y = x是一个比较困难的事情，这要求w的值必须比较精巧，才能使其与x的卷积后的结果，经过relu后刚好和y一样。如果不能输出恒等映射，则可能导致后续的性能出现下降。

Kaiming的方法是将输入x加入到输出中，如下图所示：

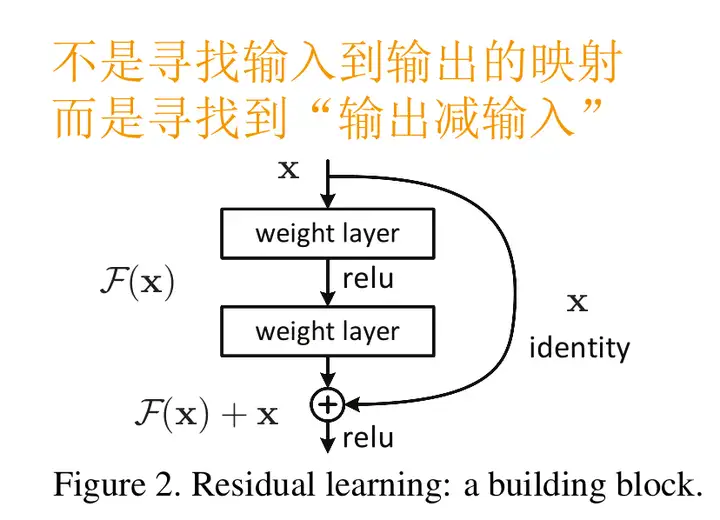
则卷积层的输出是残差，上式改为

\[y = Relu(w*x) + x \]

要想使得y=x，只需要w为0即可。是非常容易学习的。这就可以保证，即使我堆叠了过多的卷积层，至少保证性能不出现回退。

残差在ResNet与ESKF中的运用

残差在这两者中有很微妙的联系。直观的说，都是因为目标函数或者目标状态直接进行估计或者拟合太过困难，所以转为估计其变化量（即残差）。这个值相对于原始的目标，总是比较低频，动态更小的，例如ESKF中，误差状态线性化程度更好，而resnet中，恒等映射的残差在0附近。

这就揭示了一个可能被运用了很久的一种科学方法：如果直接估计或者刻画目标事物比较困难，那么可以通过估计或刻画该事物的变化量（这通常更容易观察），来侧面描绘该事物。

闲话一句，玩过PUGB的都知道，在静止场景里找到人，和找到一个运动的人，难度差太多了……这就是动态视力的作用了。

引用

1. Error State Kalman Filter V.S. EKF: 为什么EsKF更优