Error State Kalman Filter V.S. EKF: 为什么EsKF更优

本文写于2021年10月27日

背景

为什么Error-State Kalman Filter 比 Extend Kalman filter 估计出来的结果更好一些？

Extend Kalman Filter

传统的卡尔曼滤波分为Predict 和Update 部分。

Predict 部分的公式为

\[\begin{aligned} &\hat{\boldsymbol{x}}_{k \mid k-1}=f\left(\hat{\boldsymbol{x}}_{k-1 \mid k-1}, \boldsymbol{u}_{k}\right) \\ &\boldsymbol{P}_{k \mid k-1}=\boldsymbol{F}_{k} \boldsymbol{P}_{k-1 \mid k-1} \boldsymbol{F}_{k}^{\top}+\boldsymbol{Q}_{k} \end{aligned} \]

这里的\(\boldsymbol{F}_K = \frac{\partial f}{\partial \hat{x}_k}\)。

Update 部分的公式为：

\[\begin{aligned} &\tilde{\boldsymbol{y}}_{k}=\boldsymbol{z}_{k}-h\left(\hat{\boldsymbol{x}}_{k \mid k-1}\right) \\ &\boldsymbol{S}_{k}=\boldsymbol{H}_{k} \boldsymbol{P}_{k \mid k-1} \boldsymbol{H}_{k}^{\top}+\boldsymbol{R}_{k} \\ &\boldsymbol{K}_{k}=\boldsymbol{P}_{k \mid k-1} \boldsymbol{H}_{k}^{\top} \boldsymbol{S}_{k}^{-1} \\ &\hat{\boldsymbol{x}}_{k \mid k}=\hat{\boldsymbol{x}}_{k \mid k-1}+\boldsymbol{K}_{k} \tilde{\boldsymbol{y}}_{k} \\ &\boldsymbol{P}_{k \mid k}=\left(\boldsymbol{I}-\boldsymbol{K}_{k} \boldsymbol{H}_{k}\right) \boldsymbol{P}_{k \mid k-1} \end{aligned} \]

其中，\(\boldsymbol{H}_k = \frac{\partial h}{\partial \hat{x}}\)。

Error State Kalman Filter

相对于EKF直接对状态进行估计，其估计的是误差状态：

\[\tilde{x} = x - \hat{x} \]

其中\(\tilde{x}\)表示误差状态， \(x\)表示真实状态，\(\hat{x}\)表示名义状态(nominal state)，这三者的关系可以用下图表示

名义模型（Nominal Model）简单地说就是设计控制器或者进行系统分析时所用的模型，因为真实模型（True Model）在现实中一般难以获得，实际应用中都是通过系统辨识等方法得到被控对象的参数化模型（比如传递函数或状态空间方程）或者非参数化模型（比如频率响应），而这些模型严格意义上来说只是真实模型的一种近似，因此称作名义模型。——知乎

那么，ESKF的Predict过程可以写为：

\[\begin{aligned} &\hat{\boldsymbol{x}}_{k \mid k-1}=f\left(\hat{\boldsymbol{x}}_{k-1 \mid k-1}, \boldsymbol{u}_{k}\right) \\ &\boldsymbol{P}_{k \mid k-1}=\boldsymbol{F}_{k} \boldsymbol{P}_{k-1 \mid k-1} \boldsymbol{F}_{k}^{\top}+\boldsymbol{Q}_{k} \end{aligned} \]

这里的$$\boldsymbol{F}_K = \frac{\partial f}{\partial\tilde{x}_k}$$，与EKF不同。\(\boldsymbol{P}_{k \mid k-1}\) 表示的也是Error State的噪声，而非是名义状态的噪声。

ESKF的Update过程可以表示为：

\[\begin{aligned} &\tilde{\boldsymbol{y}}_{k}=\boldsymbol{z}_{k}-h\left(\hat{\boldsymbol{x}}_{k \mid k-1}\right) \\ &\boldsymbol{S}_{k}=\boldsymbol{H}_{k} \boldsymbol{P}_{k \mid k-1} \boldsymbol{H}_{k}^{\top}+\boldsymbol{R}_{k} \\ &\boldsymbol{K}_{k}=\boldsymbol{P}_{k \mid k-1} \boldsymbol{H}_{k}^{\top} \boldsymbol{S}_{k}^{-1} \\ &\tilde{\boldsymbol{x}}_{k \mid k}=0+\boldsymbol{K}_{k} \tilde{\boldsymbol{y}}_{k} \\ &\boldsymbol{P}_{k \mid k}=\left(\boldsymbol{I}-\boldsymbol{K}_{k} \boldsymbol{H}_{k}\right) \boldsymbol{P}_{k \mid k-1} \\ & \boldsymbol{x}_k = \hat{\boldsymbol{x}}_k + \tilde{\boldsymbol{x}}_k \end{aligned} \]

其中，\(\boldsymbol{H}_k = \frac{\partial h}{\partial \tilde{x}}\)。与EKF中不同。

ESKF的优点

参考文献[1]中所提到的优缺点，我尝试解释为什么ESKF会比EKF得到更加精确的结果。

优点1 ESKF对噪声的刻画更加精确

考虑到EKF的System model 为：

\[\dot{\mathbf{x}}(t)=\mathbf{f}(\mathbf{x}(t)) \]

这是一个典型的非线性系统。

根据该方程推导ESKF的Sytem model:

\[\begin{aligned} \dot{\mathbf{x}}(t)+\delta \dot{\mathbf{x}}(t) &=\mathbf{f}(\mathbf{x}(t)+\delta \mathbf{x}(t)) \\ \mathbf{f}(\mathbf{x}(t)+\delta \mathbf{x}(t)) &=\mathbf{f}(\mathbf{x}(t))+\nabla \mathbf{f}(\mathbf{x}(t))(\mathbf{x}(t)+\delta \mathbf{x}(t)-\mathbf{x}(t))+\mathcal{O}(t, \mathbf{x}(t), \delta \mathbf{x}(t)) \\ &=\mathbf{f}(\mathbf{x}(t))+\nabla \mathbf{f}(\mathbf{x}(t)) \delta \mathbf{x}(t)+\mathcal{O}(t, \mathbf{x}(t), \delta \mathbf{x}(t)) \\ \dot{\mathbf{x}}(t)+\delta \dot{\mathbf{x}}(t) &=\mathbf{f}(\mathbf{x}(t))+\nabla \mathbf{f}(\mathbf{x}(t)) \delta \mathbf{x}(t)+\mathcal{O}(t, \mathbf{x}(t), \delta \mathbf{x}(t)) \\ \delta \dot{\mathbf{x}}(t) &= F(t) \delta \mathbf{x}(t) \end{aligned} \]

这里的\(\delta x\)也表示error state，与上文\(\tilde{x}\)同义。

根据推导，因为\(F(t)=\frac{\partial f}{\partial \hat{x}}\) 与误差状态无关，因此ESKF的System Model是一个线性时变系统。其线性化程度比EKF要好很多。

从具体的图像中看，如下图所示：

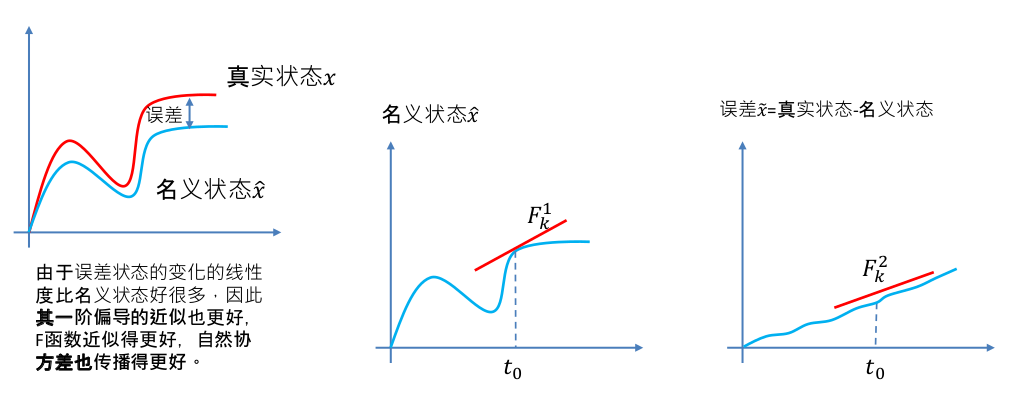
从图中可以看出，EKF在名义状态处线性化，ESKF在Error State处线性化，明显在Error State处线性化的程度更高。

ESKF的状态量更好优化

若状态量里面有旋转，则旋转通常被表示为欧拉角或四元数的形式。

在EKF框架中，若一个旋转状态量：

1. 表示为欧拉角,三个参数三个自由度,则在优化的过程中有可能出现万向节死锁的情况。
2. 表示为四元数,四个参数三个自由度,需要满足模为1的约束,优化的时候可能
   会出现协方差奇异(?)的情况。

但这些问题在ESKF中被弥补。在ESKF中，一个误差旋转变量：

1. 表示为欧拉角,在优化的过程中三个角度都在0附近,不用担心万向节死锁的情况出现。
2. 表示为四元数,当一个旋转很小的时候,四元数的w=1,同样只要优化三个参数。

\[\delta \bar{q} \simeq\left[\frac{1}{2} \delta \boldsymbol{\theta}^{T} \quad 1\right]^{T} \]

参考文献

[1] Madyastha, Venkatesh, et al. “Extended Kalman filter vs. error state Kalman filter for aircraft attitude estimation.” AIAA Guidance, Navigation, and Control Conference. 2011.