几何一致性究竟是什么？

本文写于2020年10月8日

问题

SegMatch中提到的几何一致性究竟是什么呢？

文章

• A Partitioned Approach for Efficient Graph–Based Place Recognition. 2017
• Incremental Segment-Based Localization in 3D Point Clouds.. 2018

背景

几何一致性是一种检验方法。当在全局地图(论文中称target map)中有聚类集合\(V_t={v^1_t, v_t^2, .... v_t^n}\)， 局部地图(local map)中有聚类集合\(V_l={v^1_l, v_l^2, .... v_l^m}\)， 并且通过某种匹配方法获得了\(V_l\)的对应的、在target map中的集合（称之为correspondence， 可以为一对多)，那么几何一致性检验就是为了从correspondence中挑选最有可能的匹配。

几何一致性

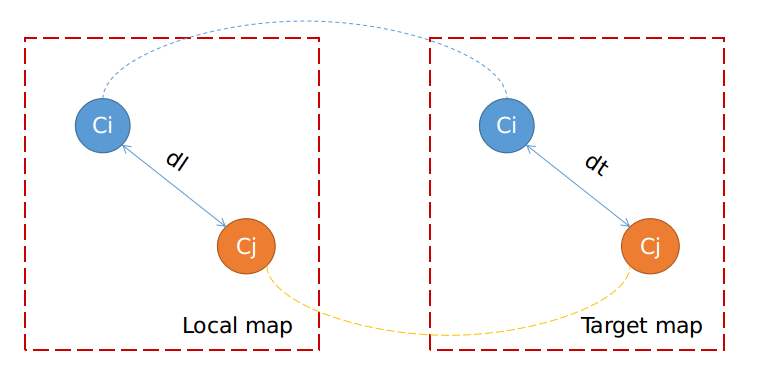
两对Correspondences，\(c_i, c_j\) 被称之为几何一致（Geometrically consistent），如果这两对segment的中心点在local map与target map中的距离之差小于一个阈值，即

\[|d_l(c_i, c_j) - d_t(c_i, c_j)| \leq \epsilon \]

其中，\(d_l(c_i, c_j)\) 与\(d_t(c_i, c_j)\) 是在local map与target map中的两对聚类的中心店的距离。如下图所示。

基于分区的一致性图构建

论文中的标题为：Partition-based consistency graph construction。

按照上一节的思路来判断并构建几何一致性的拓扑图的话，时间复杂度为\(O(n^3)\)，其中\(n\)为correspondences的数量。(这个地方存疑，我想了几遍好像都是\(O(n^2)\)的复杂度)。当全局地图比较大时，计算的时间就会很长。

因此文章一便提出了一种加速的方法，利用的是local map比global map小很多的特点。

设\(b\)为local map中的聚类中心点的集合的最小包围球形的直径，则两对corresponse\(c_i\), \(c_j\)只可能在以下情况下保持一致：

\[d_t(c_i, c_j) \leq b+\epsilon \]

其中\(\epsilon\) 是个容忍度阈值。实际上就是把上一节的公式的\(d_l(c_i, c_j)\)统一用\(d\)给放缩了。

因此可以给每个聚类的中心获得一个栅格坐标。设栅格地图的每个格子的边长为\(b+\epsilon\)，则保证了几何一致的聚类只可能在彼此相邻的栅格中，可以把原先的拓扑图快速优化成几何一致的拓扑图，如下图所示

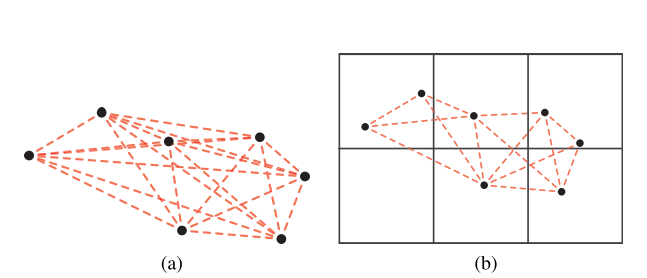
其中，两个顶点连接在一起，表示这两个顶点是几何一致的。

查找最大团

团(Clique)是图论中的概念。一个团是一个图的子集，并且这个团中的所有的顶点都是互相连接的。

最大团是指一个图中的顶点数最大的团。

在上一节的几何一致性地图中寻找最大团的意义在于，最大团表示团里所有的顶点都是几何一致的。只有当重定位时，最大团的顶点数\(N>T\)（T为一个预先设定的阈值）时才认为重定位成功。

寻找最大团的算法如下图所示。