鱼眼相机模型与标定与重映射

本文写于2019年10月21日

背景

在现有的视觉SLAM框架中，大部分是用针孔相机的图像来进行特征提取与匹配的。在一些特殊场景下有可能会需要用到鱼眼相机，因此一种操作是将鱼眼相机进行标定，转化成针孔相机的图像，然后再用SLAM框架去跑。这就涉及到了鱼眼相机的标定与像素的重映射。

鱼眼相机模型

由于鱼眼相机的径向畸变很大，并且视场角很广，一般的针孔相机模型没法描述，因而需要其他特定的模型来描述鱼眼相机的成像原理。

Mei 模型

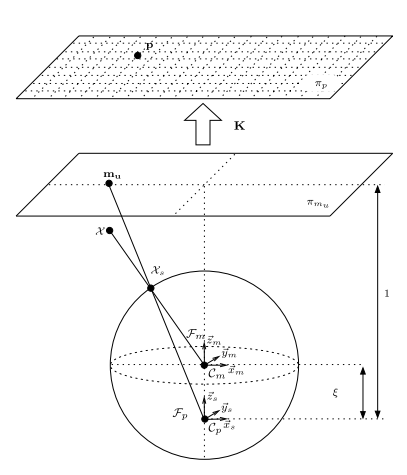
由 Christopher Mei 在^[1]中提出， 这也是VINS-mono中采用的鱼眼相机模型，亦称为Unified Camera Model， 其示意图如下所示：

其具体投影步骤为：

1. 设相机坐标系中的一个三维点为\(\chi\)，先将其坐标归一化，即将其坐标缩放到单位球面上，得到\(\chi_s = \frac{\chi}{\|\chi\|}\)。
2. 随后改变坐标系，设原来坐标系为\(C_m\)，现在坐标系为\(C_p\)， \(C_p\)相对于坐标系\(C_m\)在z轴方向上有一个负方向的平移\(\xi\)，这样导致\(\chi_s\)在新坐标系中的坐标为\((X_s, Y_s, Z_s + \xi)\)。
3. 随后将新的\(\chi_s\)投影到归一化平面上，得到三维点\(m = (\frac{X_s}{Z_s + \xi}, \frac{Y_s}{Z_s + \xi}, 1)\)。
4. 最后将归一化的平面的坐标用一个类似于针孔相机的内参的K矩阵投影到像素平面上。即最终的像素点\(p = Km\)。

所以Mei 模型需要标定的参数就是\(\xi\)以及内参矩阵K，还有在第3步之后可能存在的，和针孔相机一模一样的畸变参数\(k_1, k_2, p_1, p_2\)。这个模型的一个可用的标定工具为^[2]。

这个模型的一个缺点在于，相比于针孔相机仅仅多了一个参数\(\xi\)，因此一些图像边缘的高畸变的像素的矫正并不是很准。

PolyFisheye 模型

由港科大沈劭劼组的高文良在^[3]中提出，模型示意图如下：

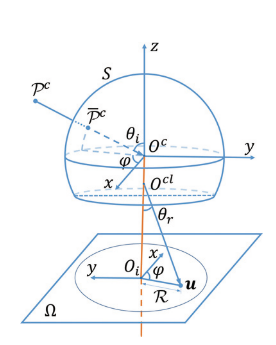
其具体投影步骤详见论文^[3:1]。

从模型图上看基本和Mei模型一模一样，唯一的不同是，假设空间点\(P^c\)最终投影得到的像素点为\(u\)，他们认为\(u\)到光心\(O_i\)的距离\(R\)并不是直接等于沿着\(\theta_r\)方向上投影过来的大小，而是和\(O_{cl}\)到\(u\)的距离存在一个关于\(\theta\)的七次多项式的多项式倍数关系。这样就相比Mei模型多了七个参数来刻画鱼眼相机，自然就更准了。

像素重映射

当相机标定完后，需要将鱼眼相机的像素重新映射到单目相机上。

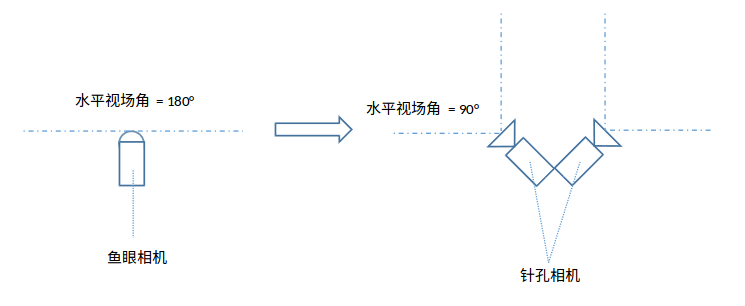
其实只是建立虚拟的针孔相机上的每个像素与鱼眼相机的每个像素的映射关系，即可直接用OpenCV的remap函数双线性插值得到针孔相机的图像。其具体步骤为：

1. 先确定虚拟针孔相机的内参（fx, fy, cx, cy)与相对于鱼眼相机的外参。
2. 对于虚拟相机的每个像素点\(p_{pinhole}\)，将像素点反投影到归一化平面，得到三维点\(p_{3d}\)（z=1）。
3. 将三维点根据鱼眼相机模型，投影到鱼眼相机上，得到鱼眼相机上的像素点\(p_{fisheye}\)。
4. 如此，便建立了针孔相机的像素点与鱼眼相机的像素点的映射关系，根据映射关系取鱼眼相机的像素即可。

一些细节

• 虚拟相机的视场角是由虚拟相机内参(fx, fy)控制的，fx=width / 2时视场角刚好为90度。width为图像的像素宽度。
• 映射关系可以先算出来做成Lookup table，然后处理鱼眼图像时再直接查表即可。

代码

详见^[4]。

---

1. Single View Point Omnidirectional Camera Calibration from Planar Grids，ICRA 2007 ↩︎

2. https://github.com/hengli/camodocal ↩︎

3. Dual-Fisheye Omnidirectional Stereo, IROS 2017 ↩︎ ↩︎

4. https://github.com/EpsAvlc/EpsAvlc_toys/tree/master/fisheye_to_pinhole ↩︎