相机-激光雷达在线标定
本文写于2019年5月3日
相机与雷达的在线标定
其实就是手眼标定。而且这个可以推广开去,做任何可以求出Odometry的传感器之间的标定。
PAPER
LiDAR and Camera Calibration using Motion Estimated by Sensor Fusion Odometry(IROS2018)
OUTLINE
- 从相机的无尺度信息(scaleless)的运动以及Lidar有尺度的运动中得到一个初步的相机与LiDAR的外参。
- 用1得到的外参与LiDAR的点云来重新计算相机的运动。
- 再用2得到的motion重新估计外参。循环1-3直至收敛。
METHODOLOGY
初始标定数据估计
-
首先计算LiDAR的运动。通过一个效率较高的ICP算法来计算LiDAR的odometry。
-
然后计算Camera的运动。通过特征点匹配算法得到相机的odometry。
-
外参的获得。基本模型是手眼标定(hand-eye calibration)的模型。设相机的运动为\(R^i_{cam}, \overline{t}^i_{cam}\)。因为相机得到的t是没有尺度的,所以有个上划线表示估计值。设LiDAR的运动为 \(R^i_{lid}, \overline{t}^i_{lid}\),则这两个运动满足以下关系:
\[\boldsymbol{R}_{c a m}^{i} \boldsymbol{R}=\boldsymbol{R} \boldsymbol{R}_{l i d}^{i} \]\[\boldsymbol{R}_{c a m}^{i} \boldsymbol{t}+s^{i} \overline{\boldsymbol{t}}_{c a m}^{i}=\boldsymbol{R} \boldsymbol{t}_{l i d}^{i}+\boldsymbol{t} \]其中\(s^i\)是一个缩放因子,将求得的相机的\(\overline{t}^i_{cam}\)缩放到真实值。而\(R,t\)是相机与激光雷达的外参。这两个式子的推导见下文的推导部分。
那么初始的\(R\)可以由式(1)推得:
\[\boldsymbol{k}_{c a m}^{i}=\boldsymbol{R} \boldsymbol{k}_{l i d}^{i} \]其中\(k_{cam}^i\) 与\(k_{lid}^i\)为旋转矩阵\(R^i_{cam}, R^i_{lid}\)的旋转轴,可以通过将旋转矩阵奇异值分解,求其特征值为1的特征向量而得。那么\(R\)的初始解可以通过求解线性方程(3)得到,\(t\)则通过求解式(2)得出。解得\(R\)的初始解后,还进行了对\(R\)的优化。通过对下式的非线性优化得到较为好的\(R\)。
\[\boldsymbol{R}=\underset{\boldsymbol{R}}{\arg \min } \sum_{i}\left|\mathbf{R}_{c a m}^{i} \mathbf{R}-\mathbf{R} \mathbf{R}_{l i d}^{i}\right| \]
迭代优化相机的运动估计和传感器标定
在得到了一个初始的外参后,可以做以下几件事。
-
优化相机的运动估计。
由于激光雷达测得的三维点很准确,所以可以用其三维点来优化单纯凭借特征点匹配得到的相机运动。
如下图所示。首先根据上文得到的齐次变换矩阵将激光雷达的三维点投影到相机坐标系中,假设投影后相机坐标系有一个点为\(P\)(由激光雷达点云得到的)。根据相机内参计算出\(P\)点的像素位置,然后利用KLT光流法计算该点在时刻2(图中为camera 2)时的像素位置,这样就得到了在时刻1(图中为camera 1)的三维点与时刻2的二维点的匹配,用PnP可以求解出时刻一到时刻二的相机运动。注意到此时求出的相机运动已经是有尺度的了。
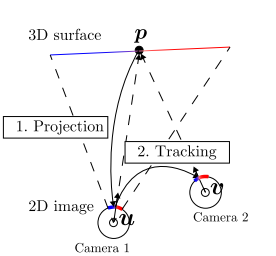
上文求出的运动作为下式这个非线性优化的初始值,得到最佳解的齐次变换。
上式就是一个重投影误差。
- 优化外参。在得到比较精确的相机运动后,可以再代入式(4)求出一个更好的外参\(R\)。而根据式(3)有
所以通过优化以下损失函数可得最优的外参\(t\)。
在线标定所需要的运动要求
方法论的东西就是上文那些,论文里其他部分是讲怎么样的运动可以使得标定效果更好,总结如下:
- 在用激光雷达投影到相机,优化相机运动那里,\(t_{cam}\)小可以使运动估计更准确。
- 环境中的物体表面最好比较光滑,这样会使激光雷达测得的深度变化不大,对重投影那里有帮助。
- 对相机做角度比较大的旋转更容易标定成功,因此鱼眼相机比普通相机好,因为鱼眼相机视角广,旋转时不容易丢失特征点。
DERIVATION
以下是对文章中一些式子的推导。
-
式(1)的推导如下:设i时刻激光雷达坐标系中某个三维点为\(p_{lid}^i\),则其在相机坐标系中为
\[p_{cam}^{i} = Rp_{lid}^i + t \]在t=0时刻,该点在相机坐标系中的关系为
\[p_{cam}^0 = R_{cam}^ip_{cam}^{i} + s^i\overline{t}^i_{cam} =R_{cam}^iRp_{lid}^i + (R_{cam}^it + s^i\overline{t}^i_{cam}) \]其中\(p_{lid}^i\)与\(p_{lid}^0\)的关系为
\[p_{lid}^0 = R_{lid}^ip_{lid}^{i} + t^i_{lid} \]而该点在t=0时刻,其在激光雷达坐标系中的坐标与在相机坐标系的坐标关系有
\[p_{cam}^{0} = Rp_{lid}^0 + t=RR_{lid}^ip_{lid}^{i} + (Rt_{lid}^i + t) \]则有
\[RR_{lid}^ip_{lid}^{i} + (Rt_{lid}^i + t) = R_{cam}^iRp_{lid}^i + (R_{cam}^it + s^i\overline{t}^i_{cam}) \\ \]由于两边括号内是平移量,必然是相等的,只看旋转的话有
\[RR_{lid}^ip_{lid}^{i} = R_{cam}^iRp_{lid}^i \rightarrow RR^i_{lid}=R^i_{cam}R \]而式子(2)是只看平移量相等得到的。则两个式子得证。
-
式(3)的推导:在推导该式之前,首先推导一个定理:
\[\operatorname{Rot}(R \boldsymbol{k}, \theta)=R \operatorname{Rot}(\boldsymbol{k}, \theta) R^{-1} \]其中上式的\(Rot\)函数是将轴角\(k,\theta\)转化为旋转矩阵的函数。
首先理解一个概念,齐次变换矩阵其实可以表示为一个坐标系的原点坐标,举例来说:
\[T=\left[ \begin{array}{llll}{n_{x}} & {o_{x}} & {a_{x}} & {p_{x}} \\ {n_{y}} & {o_{y}} & {a_{y}} & {p_{y}} \\ {n_{z}} & {o_{z}} & {a_{z}} & {p_{z}} \\ {0} & {0} & {0} & {1}\end{array}\right] \]可以理解为一个原点在\(p_x, p_y, p_z\),而三个坐标轴方向与向量\(n, o, a\)相同的坐标系(考虑其与单位矩阵相乘后的情况)。同时,我们将原点没动,相对于单位矩阵只有旋转的齐次变换表示为\(R\)。理解了这个概念后,假设某一时刻存在坐标系\(R_0\),下一时刻它被旋转矩阵\(Rot(k,\theta)\)旋转到坐标系\(R_1\)中。则有
\[Rot(k,\theta)R_0=R_1 \]比较难理解的是这一步:对上面的式子两边同时乘以R有
\[Rot(Rk,\theta)RR_0=RR_1 \]对于左边,我的理解是将某个旋转了\(Rot(k,\theta)\)的坐标系在旋转R,等同于先把这个坐标系旋转R,在旋转\(Rot(Rk,\theta)\)。这个画个图会比较容易明白。
上式可变形为
\[Rot(Rk,\theta)=RR_1R_0^{-1}R \\ = RRot(k,\theta)R \]则得证。
回到式(2)中:
\[Rot(k_{cam}^i, \theta_{cam}^i)R=RRot(k_{lid}^i, \theta_{lid}^i) \]将式(3)代入上式,等式左边为
\[Rot(Rk_{lid}^i, \theta_{cam}^i)R=(RRot(k_{lid}^i,\theta_{cam}^i)R^{-1})R\\=RRot(k_{lid}^i, \theta_{cam}^i) \]又因为激光雷达与相机是刚性连接,所以有\(\theta_{cam}^i = \theta_{lid}^i\)。则式(2)得证。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号