MATLAB实现灰度图像二维傅里叶变换

一、基础实现流程

1. 图像读取与预处理

% 读取图像并转换为灰度图
img = imread('lena.jpg');
gray_img = rgb2gray(img);  % 转换为灰度图像 

% 数据类型转换（关键步骤）
img_double = im2double(gray_img);  % 转换为double类型

2. 二维傅里叶变换

% 执行二维傅里叶变换
F = fft2(img_double);      % 傅里叶变换 
F_shifted = fftshift(F);   % 频谱中心化

3. 频谱可视化

% 计算幅度谱（对数变换增强显示）
magnitude = log(1 + abs(F_shifted));  % 对数变换 

% 计算相位谱
phase = angle(F_shifted);  % 相位信息 

% 显示结果
figure;
subplot(131), imshow(gray_img), title('原图');
subplot(132), imshow(magnitude, []), title('幅度谱');
subplot(133), imshow(phase, []), title('相位谱');  % 使用HSV映射更佳

二、原理

1. 傅里叶变换特性

• 零频分量：位于频谱中心，代表图像整体亮度
• 低频分量：靠近中心，对应平滑区域
• 高频分量：远离中心，对应边缘和噪声

2. 频谱中心化原理

通过fftshift将零频分量移动到频谱中心，便于观察低频成分分布：

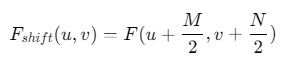
3. 对数变换必要性

原始频谱动态范围过大（如\(10^5\)到\(10^{−3}\)），直接显示会导致细节丢失。对数变换公式：

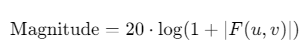
三、进阶功能实现

1. 频域滤波（低通滤波示例）

% 创建低通滤波器
[M,N] = size(gray_img);
D0 = 50;  % 截止频率
[X,Y] = meshgrid(-N/2:N/2-1, -M/2:M/2-1);
D = sqrt(X.^2 + Y.^2);
H = double(D <= D0);  % 理想低通滤波器

% 应用滤波
G = H .* F_shifted;    % 频域相乘
g = ifftshift(G);      # 逆中心化 
g = ifft2(g);          # 逆变换

% 显示结果
figure, imshow(g, []), title('低通滤波后图像');

2. 频谱增强显示

% 零填充提升分辨率
F_padded = fft2(img_double, 2*M, 2*N);  # 双边零填充 
F_shifted = fftshift(F_padded);

% 三维频谱显示
[X,Y] = meshgrid(1:size(F_shifted,2), 1:size(F_shifted,1));
surf(X,Y,log(1+abs(F_shifted)), 'EdgeColor','none');
shading interp;
xlabel('X频率'), ylabel('Y频率'), zlabel('幅度');

四、调试技巧

1. 坐标系验证

% 验证平移特性
img_shifted = circshift(gray_img, [50,30]);
F_shifted = fft2(img_shifted);
[~, loc] = max(abs(F_shifted(:)));  % 应出现在(50,30)附近

2. 性能优化

% 使用GPU加速（需Parallel Computing Toolbox）
img_gpu = gpuArray(img_double);
F_gpu = fft2(img_gpu);
F_shifted = fftshift(F_gpu);

五、常见问题处理

现象	解决方案	参考来源
频谱全黑	检查对数变换参数，增加偏移量
相位谱显示异常	使用HSV色彩映射代替灰度
逆变换图像模糊	确保使用完整复数结果进行逆变换
计算内存溢出	采用分块处理或降低图像分辨率

参考代码 灰度图像的二维傅里叶变换 www.youwenfan.com/contentcnj/69842.html

六、完整工程结构

FFT_Demo/
├── Src/
│   ├── main.m          # 主程序
│   ├── fft_utils.m     # 傅里叶工具函数
│   └── filters/        # 滤波器库
├── Images/
│   ├── input.jpg       # 输入图像
│   └── output/         # 处理结果
└── README.md

---

七、扩展应用

1. 图像复原：通过频域滤波去除周期性噪声
2. 特征提取：分析纹理图像的频域能量分布
3. 压缩感知：保留主要频率成分实现图像压缩

通过上述方案，可深入理解灰度图像的频域特性，并应用于图像处理、计算机视觉等领域。建议结合MATLAB的信号处理工具箱进行高级分析，并使用imshowpair函数对比空域与频域处理效果。