CSP-S 2022 T4 题解
简述题意
给一颗 \(n\) 个点的树,每个点有点权 \(v_i\)。有 \(q\) 次询问,每次给出 \((u,v)\),从 \(u\) 开始,每步只能走不超过 \(k\) 条边,走一步的代价是终点的点权,\(v_u\) 也要算在移动的代价中,问 \(u\rightarrow v\) 的最小代价。
数据范围:\(1\le n,q\le 2\times 10^5,1\le v_i\le 10^9,1\le k\le 3\)。
算法分析
考虑 dp,用 \(d_{i,j}\) 表示 \(i,j\) 在树上的距离,\(f_{i,j}\) 表示满足最后一步的终点为 \(\forall x\in V,d_{x,v}\le d_{i,v}\and d_{x,i}=j\) 的方案,就可以得出 \(O(nkq)\) 的暴力。
但发现直接在链上 dp 连样例都过不了,因为 \(x\) 不一定是链上的点,比如下图中绿边表示询问的链,红边可能才是最优的转移:
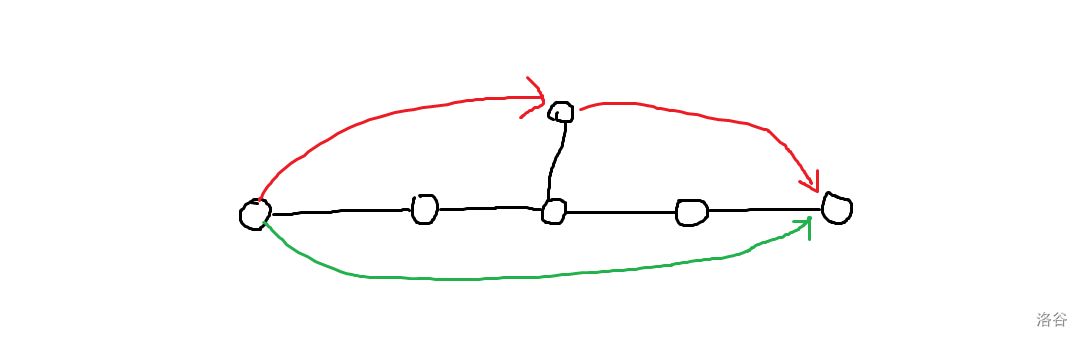
分类讨论一下不难证明,只有 \(k=3\) 时最优解才有可能跳到路径之外的点上,对 \(k\) 分类,我们可以写出 dp 方程:
- \(k=1\)
\(f_{i,0}=f_{i-1,0}+v_i\)。(这里进行了重编号,我们认为询问的链上的点的编号是连续的。)
- \(k=2\)
- \(k=3\)
注意到 \(f_{i-1,1}\) 已经包含了 \(f_{i-2,0}\) 的情况,无需更多的分类讨论。
直接转移就是 \(O(nqk)\) 的。注意到 dp 中 \(f_i\) 的取值只和 \(f_{i-1}\) 处的取值有关,可以用矩阵优化。\(\min\) 运算并不是矩阵中应该有的算符,所以我们需要定义新的矩阵乘法:
因为 \(+\) 关于 \(\min\) 有分配律,所以 \((\min,+)\) 的矩阵乘法依然满足结合律。
对于不同的 \(k\) 分别构造转移矩阵,记点 \(i\) 对应的转移矩阵为 \(M_i\)。
- \(k=1\)
- \(k=2\)
- \(k=3\)
那么我们的 dp 过程可以变为:
一开始有:
用树链剖分和线段树维护每条重链上自下而上和自上而下的 \(M_i\) 的乘积转移即可。
代码实现
为了方便,我的代码中把三种矩阵都填充为了 \(3\times3\) 的矩阵,在 \((\min,+)\) 的意义下,我们只需要用 \(+\infty\) 填充空位就可以了,此时单位矩阵为 \(\left[\begin{matrix}0 & +\infty & +\infty\\+\infty & 0 & +\infty\\+\infty & +\infty & 0\end{matrix}\right]\)。
出于个人习惯,在代码中采用的转移方式是 \(M_{i}F_{i-1}=F_i\),这只需要转置上文中出现的矩阵即可。
如果从 \(F_1\) 开始转移的话不能乘 \(M_1\),需要细节处理。不过从 \(F_0=\left[\begin{matrix}0\\+\infty\\+\infty\end{matrix}\right]\) 开始转移就没有这个必要了。
const ll inf=1e18;
namespace sol
{
const int N=2e5+5,M=2e5+5;
int n,Q,k;
ll v[N];
int fa[N],top[N],son[N],siz[N],dep[N],dfn[N],dfn_cnt,rdfn[N];
vector<int> e[N];
ll f[N][3];
ll ex[N];
class dp
{
public:
ll a[3][3];
inline ll *operator[](int i) { return a[i]; }
inline const ll *operator[](int i) const { return a[i]; }
dp()
{
a[0][0]=0,a[0][1]=inf,a[0][2]=inf;
a[1][0]=inf,a[1][1]=0,a[1][2]=inf;
a[2][0]=inf,a[2][1]=inf,a[2][2]=0;
} dp(ll x) { for(int i=0;i<3;++i) for(int j=0;j<3;++j) a[i][j]=x; }
dp(ll x00,ll x01,ll x02,ll x10,ll x11,ll x12,ll x20,ll x21,ll x22)
{
a[0][0]=x00,a[0][1]=x01,a[0][2]=x02;
a[1][0]=x10,a[1][1]=x11,a[1][2]=x12;
a[2][0]=x20,a[2][1]=x21,a[2][2]=x22;
}
friend dp operator * (dp a,dp b)
{
dp c(inf);
for(int i=0;i<3;++i)
for(int j=0;j<3;++j)
for(int k=0;k<3;++k)
c[i][j]=min(c[i][j],a[i][k]+b[k][j]);
return c;
}
};
class node
{
public:
int c[2];
dp up,down;
node()=default;
}; node s[N<<2]; int cnt,rt;
#define ls(x) s[x].c[0]
#define rs(x) s[x].c[1]
#define all rt,1,n
#define mid ((l+r)>>1)
#define L(x) ls(x),l,mid
#define R(x) rs(x),mid+1,r
inline void pushup(int x)
{
if(ls(x))
s[x].up=s[rs(x)].up*s[ls(x)].up,
s[x].down=s[ls(x)].down*s[rs(x)].down;
}
inline void build(int &x,int l,int r)
{
if(!x) x=++cnt;
if(l==r)
{
int u=rdfn[l];
if(k==1) s[x].up=s[x].down=dp(v[u],inf,inf,inf,inf,inf,inf,inf,inf);
if(k==2) s[x].up=s[x].down=dp(v[u],v[u],inf,0,inf,inf,inf,inf,inf);
if(k==3) s[x].up=s[x].down=dp(v[u],v[u],v[u],0,ex[u],inf,inf,0,inf);
return;
} build(L(x)),build(R(x)),pushup(x);
}
inline dp upquery(int x,int l,int r,int ql,int qr)
{
if(l==ql&&r==qr) return s[x].up;
if(qr<=mid) return upquery(L(x),ql,qr);
if(ql> mid) return upquery(R(x),ql,qr);
return upquery(R(x),mid+1,qr)*upquery(L(x),ql,mid);
}
inline dp downquery(int x,int l,int r,int ql,int qr)
{
if(l==ql&&r==qr) return s[x].down;
if(qr<=mid) return downquery(L(x),ql,qr);
if(ql> mid) return downquery(R(x),ql,qr);
return downquery(L(x),ql,mid)*downquery(R(x),mid+1,qr);
}
inline dp up(int x,int y)
{
if(dfn[x]<dfn[y]) return upquery(all,dfn[x],dfn[y]);
return upquery(all,dfn[y],dfn[x]);
}
inline dp down(int x,int y)
{
if(dfn[x]<dfn[y]) return downquery(all,dfn[x],dfn[y]);
return downquery(all,dfn[y],dfn[x]);
}
inline dp upline(int x,int f)
{
dp b;
while(top[x]!=top[f])
{
b=b*up(x,top[x]);
x=fa[top[x]];
}
return b*up(x,f);
}
inline dp downline(int x,int f)
{
static vector<int> tmp;
if(!tmp.empty()) tmp.clear();
dp b;
while(top[x]!=top[f])
{
tmp.emplace_back(x);
x=fa[top[x]];
} if(x!=f) b=b*downquery(all,dfn[f]+1,dfn[x]);
reverse(tmp.begin(),tmp.end());
for(auto x:tmp) b=b*down(x,top[x]);
return b;
} inline int lca(int x,int y);
inline ll line(int x,int y)
{
if(x==y) return v[x];
int l=lca(x,y);
if(x==l) swap(x,y);
dp tmp=upline(y,l)*downline(fa[x],l);
return tmp[0][0]+v[x];
}
inline void init()
{
f[0][0]=f[0][1]=f[0][2]=inf;
for(int i=1;i<=n;++i)
{
ex[i]=inf;
for(int to:e[i])
ex[i]=min(ex[i],v[to]);
} build(all);
}
inline void dfs1(int u,int f)
{
fa[u]=f,dep[u]=dep[f]+1,siz[u]=1;
for(int v:e[u])
if(v!=f)
{
dfs1(v,u); siz[u]+=siz[v];
if(siz[v]>=siz[son[u]]) son[u]=v;
}
}
inline void dfs2(int u,int tp)
{
top[u]=tp,dfn[u]=++dfn_cnt,rdfn[dfn_cnt]=u;
if(son[u]) dfs2(son[u],tp);
for(int v:e[u])
if(v!=fa[u]&&v!=son[u])
dfs2(v,v);
}
inline int lca(int x,int y)
{
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]]) swap(x,y);
x=fa[top[x]];
} return dep[x]<dep[y]?x:y;
}
inline void solmain()
{
read_(n),read_(Q),read_(k);
for(int i=1;i<=n;++i) read_(v[i]);
for(int i=1,u,v;i<n;++i)
read_(u),read_(v),
e[u].emplace_back(v),
e[v].emplace_back(u);
dfs1(1,0);
dfs2(1,1);
init();
ll as;
for(int i=1,x,y;i<=Q;++i)
{
read_(x),read_(y);
as=line(x,y);
cout<<as<<'\n';
}
}
}
个人认为这题做 CSP-S T4 有点简单了,比较套路。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号