Planar Graph

如果一个图 \(G=(V,E)\) 可以被画在一个欧几里得平面上并且边不交叉（端点不算），那么 \(G\) 就是可平面图的（\(\text{planar}\)），平面图有一些奇妙的性质，不过本文重点关注如何判断一个图是否是可平面图。

\(\#\) 可平面图（\(\text{planar graph}\)）和平面图（\(\text{plane graph}\)）是不同的，后者需要绑定具体的嵌入（\(\text{embed}\)）方法。

Koratowski's Theorem

Euler's Formula

\(\chi=V-E+F\) 是拓扑不变量。

其中 \(V\) 是点数，\(E\) 是边数，\(F\) 是面数（面就是一些不交的边构成的极小封闭图）。

看不懂没关系，这里只需要证明对于欧几里得平面上的连通可平面图，有 \(\chi=2\) 就好了。（更多不必要的数学内容可以看这里）

只有一个点的时候，整个平面是一个面，有 \(V=1,F=1\)，此时 \(\chi=2\)。

然后我们考虑归纳，假设 \(V=k\) 时，\(\chi\equiv2\)，试着证明 \(V=k+1\) 时，\(\chi\equiv2\)。

然后注意到新加一个点 \(x\)，其至少有一个邻居 \(y\)（否则不连通），此时贡献是 \(0\)，然后假设 \(x\) 还有 \(l\) 个邻居 \(z_1,z_2\ldots z_l\)，因为是 \(\text{planar graph}\)，\(x-y-z_i\) 恰好描述了 \(l\) 个新的面，而增加了 \(x-z_i\) 这样 \(l\) 条边，贡献还是 \(0\)，于是 \(V=k+1\) 的时候，还是有 \(\chi=2\)。

逆否命题也是真的，即 \(\chi(G)\neq2\Rightarrow G \text{ is not planarable}\)。

于是我们可以轻易地得到一个约束，对于可平面图，满足 \(|E|\le 3|V|-6\)。

非平面图的例子

\(K_5\) 不是可平面图。

\(K_5\) 就是阶为 \(5\) 的完全图。

计算 \(\chi(K_5)\)，有 \(V=5,E=\binom{5}{2}=10,F=1+\binom{5}{3}=11\)，于是 \(\chi(K_5)=6\)，可以知道 \(K_5\) 不是可平面图。

\(K_{3,3}\) 不是可平面图。

\(K_{3,3}\) 是完全二分图。证法和上面差不多，考虑 \(V=6,E=3\times 3=9\)，如果 \(K_{3,3}\) 是可平面图的，那么应该有 \(V-E+F=2\)，得到 \(F=5\)。

用 \(f_i\) 表示第 \(i\) 个面，用 \(e(f_i)\) 表示这个面的边数。显然，平面图中，每条边恰好属于两个不同的面，于是 \(\sum\limits_{i=1}^Fe(f_i)=2E\)，由此可以得到每个面的平均边数 \(\overline{e}(f)=\frac{18}{5}<4\)。而 \(K_{3,3}\) 是二分图，没有奇环，偶环的长度至少为 \(4\)，又知道一个面一定是环，矛盾。

Koratowski's Theorem

\(G\) 不是可平面的，当且仅当 \(G\) 的一个子图同胚于 \(K_5\) 或 \(K_{3,3}\)。

图的同胚是指，在一条边上插入一个顶点，或把一个度数恰好为 \(2\) 的顶点删去，然后连接其原本的邻居，通过这样的若干次操作可以变得同构。

必要性是显然的，我们只需要证明充分性。

Preparation

不连通的图可平面显然等价于其各个连通块都可平面，所以可以不失一般性地，假设 \(G\) 连通。下面考虑反证法。

因为树显然是可平面的，所以不可平面图一定是添加了某条边后变得不可平面的，于是我们可以选取一个极小的不含 \(K_5\) 或 \(K_{3,3}\) 同胚子图的不可平面图 \(G\)，这里的极小是说，\(G\) 的所有子图要么是平面图，要么含有 \(K_5\) 或 \(K_{3,3}\) 同胚子图（这显然是不可能的）。

如果一个点度数恰好为 \(2\)，那么通过同胚操作可以删去这个点，不难想到这不会影响可平面性。

如果一个点度数恰好为 \(1\)，那么我们直接删去这个点，显然得到的新图还是不可平面的。

如果 \(G\) 中有一条割边，那么 \(G\) 至少可以被分成两个边双，其中至少一个是不可平面的，我们分别讨论即可。类似地，可以说明 \(G\) 中没有割点。

于是，不失一般性，可以设 \(\forall v\in V,d(v)\ge 3\)，且 \(G\) 中没有割点和割边（也就是 是 \(2-\)连通且 \(2-\)边连通的）。

3-connection

接下来，我们加强结论，试着说明 \(G\) 是 \(3-\)连通的。

考虑反证法，假设 \(G\) 有一个点割集为 \(\{x,y\}\)。

接着我们考虑一个被称为 \(\text{lobe}\) 的结构，具体一点，\(S\subseteq V\)，一个 \(S-\text{lobe}\) 是 \(S\) 和 \(G\setminus S\) 中任意一个连通块的并。\(\text{naive}\) 一点地说，就是删去这个割集 \(\{x,y\}\) 后，我们选择一个被割断的连通块和 \(\{x,y\}\) 拼成一个类似点三的东西。

现在考虑所有的 \(\text{lobe}\)，记为 \(G_1,G_2\ldots G_m\)。因为 \(\{x,y\}\) 是点割集，所以 \(m\ge 2\)，这导出 \(|G_i|<|G|\)。因为 \(G\) 是极小的不含 \(K_5\) 或 \(K_{3,3}\) 同胚子图的不可平面，有两种情况。

1. \(G_i\) 是可平面图；
2. \(G_i\) 含有 \(K_5\) 或 \(K_{3,3}\) 的同胚子图。

若所有 \(G_i\) 都是可平面图，对于只和 \(x,y\) 连接的连通块，可以用任意小的空间将其画下，然后保证别的边都在其之外；对于同时连接 \(x,y\) 的连通块，将其依次平面化，然后把和 \(x,y\) 连接的边画到外面，大概是下图的情况

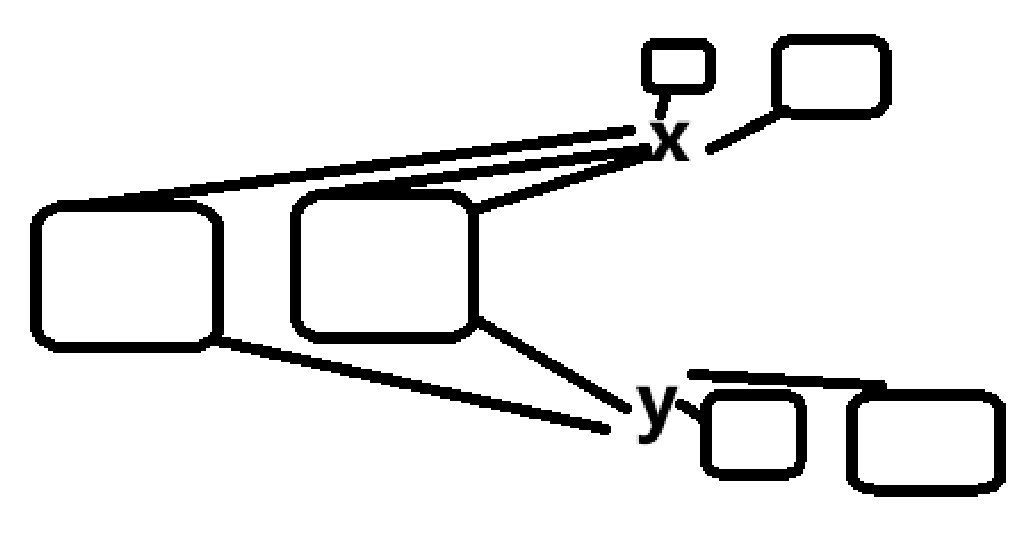
于是可以导出 \(G\) 是可平面图，矛盾。

若 \(G_i\) 含有 \(K_5\) 或 \(K_{3,3}\) 的同胚子图，若 \(x-y\in E\)，那么 \(G\) 也含有一个这样的同胚子图，矛盾。若 \(x-y\not\in E\)，那么根据连通性，存在一条 \(G_i\) 中的简单路径 \(p:x\to y\)，此时，把这条路径缩为一条边（其实按照定义是给 \(K_{3,3}\) 或 \(K_5\) 中加点），可以得出 \(G\) 还是含有一个这样的同胚子图，矛盾。

综上，\(G\) 不存在大小为 \(2\) 的点割集，也就是 \(G\) 是 \(3-\)连通的。

Proof

现在选取一个极小的不含 \(K_5\) 或 \(K_{3,3}\) 同胚子图的不可平面图 \(G\)，也就是对于其中任意一条边 \(e=u-v\)，根据 \(G-e\) 都会是平面图（如果有这样的边，我们就贪心地删，最后一定可以得到极小的不可平面图）。

同时，因为 \(G\) 是 \(3-\)连通的，\(G-e\) 至少是 \(2-\)连通的。于是在 \(G-e\) 中，\(u,v\) 在一个环 \(C\) 上。因为 \(G-e\) 是可平面图，所以可以被划分成若干不交的面，一些面被放在 \(C\) 内部，一些在外部，这样的放法显然是不唯一的，为了理解的方便，我们把不同的放法视为本质不同的，然后选择一个在 \(C\) 内部的面最多的放法（从所有可能的 \(C\) 和放法中）。

假设 \(C:v_0-v_1-v_2-\cdots-v_k-v_0,v_0=v_k=u,v_{l}=v\)，其中 \(0<l<k\)。

Lemma 1

断言不存在 \(v_i\to v_j\) 的路径在 \(C\) 外，对于 \(0\le i<j\le l\lor l\le i<j\le k\)，否则 \(v_i-v_{i+1}-\cdots-v_j\to v_i\) 是一个在 \(C\) 外的面，此时 \(v_0\to v_i\to v_j\to v_k\) 可以比 \(C\) 额外多包含这个面。

然后，\(C\) 外一定存在路径，否则可以把 \(u-v\) 连接在 \(C\) 外，保证依然是平面图，于是这只能是 \(v_i\to v_j\) 的路径，满足 \(0<i<l<j<k\)。

如图

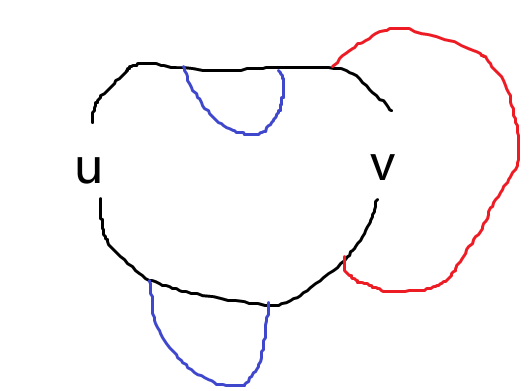
我们说明了一定不存在蓝色的路径，而一定存在红色的路径。

Lemma 2

然后对于 \(v_i\to v_j\) 路径（图中红色路径）上的一个点 \(x\)，可以是端点，不存在一个 \(y\) 在 \(v_i\to v_j\to v\to v_i\) 面（图中红色和 \(v\) 所在黑色部分构成的面）外部有 \(x\to y\) 的路径（见下图蓝色），否则会有一个包含更多内部面的环 \(C^\prime\)（见下图绿色）。

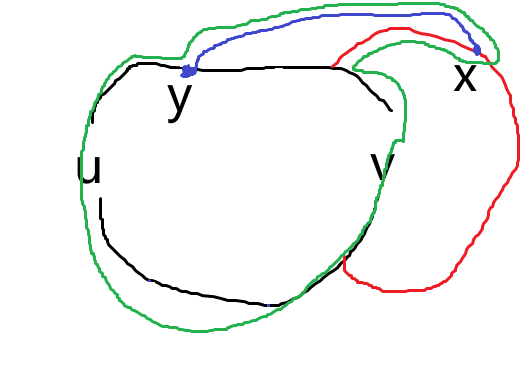
为了我画图方便，下面把 \(v_i,v_j\) 依次记为 \(x,y\)。

Solution

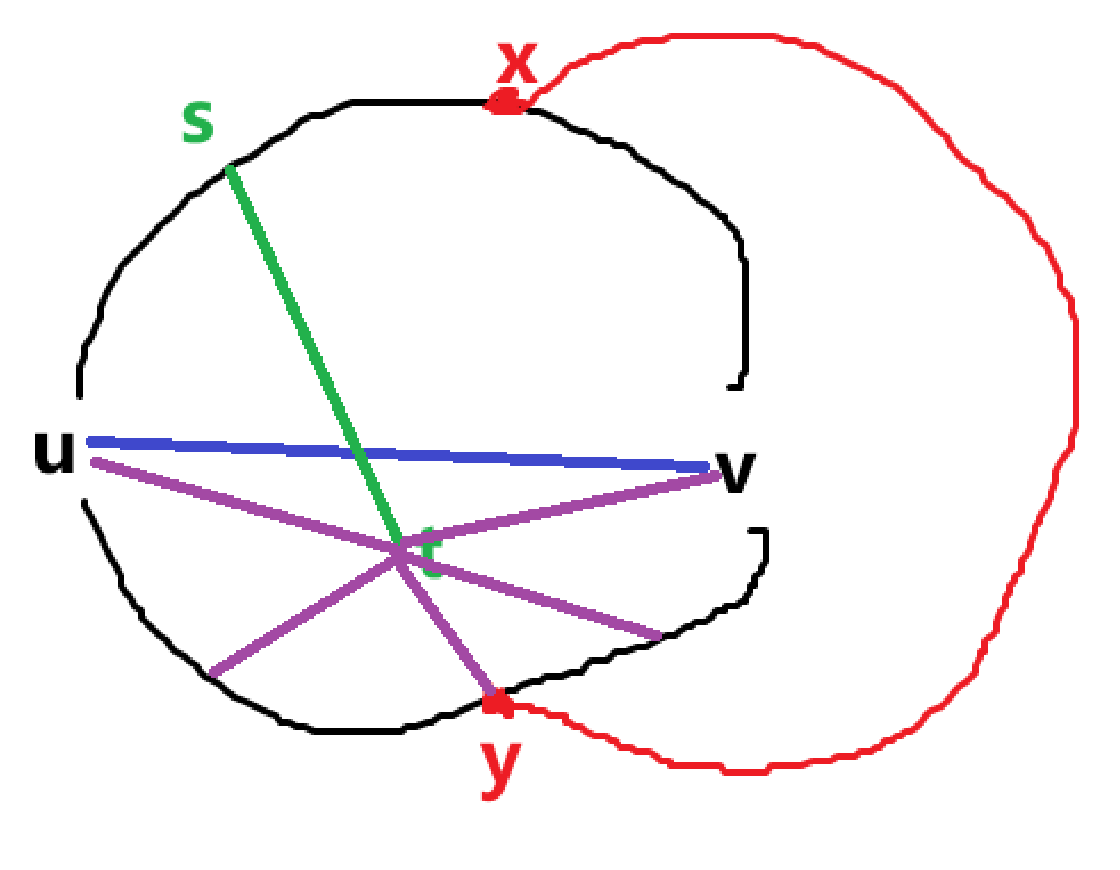
现在我们知道加入 \(u-v\) 这条边之后图就不可平面了，也就是我们不能在 \(C\) 内部把 \(u-v\) 连起来（外面显然已经不行了），也就是下图蓝边一定会和一条已经有的边交叉。

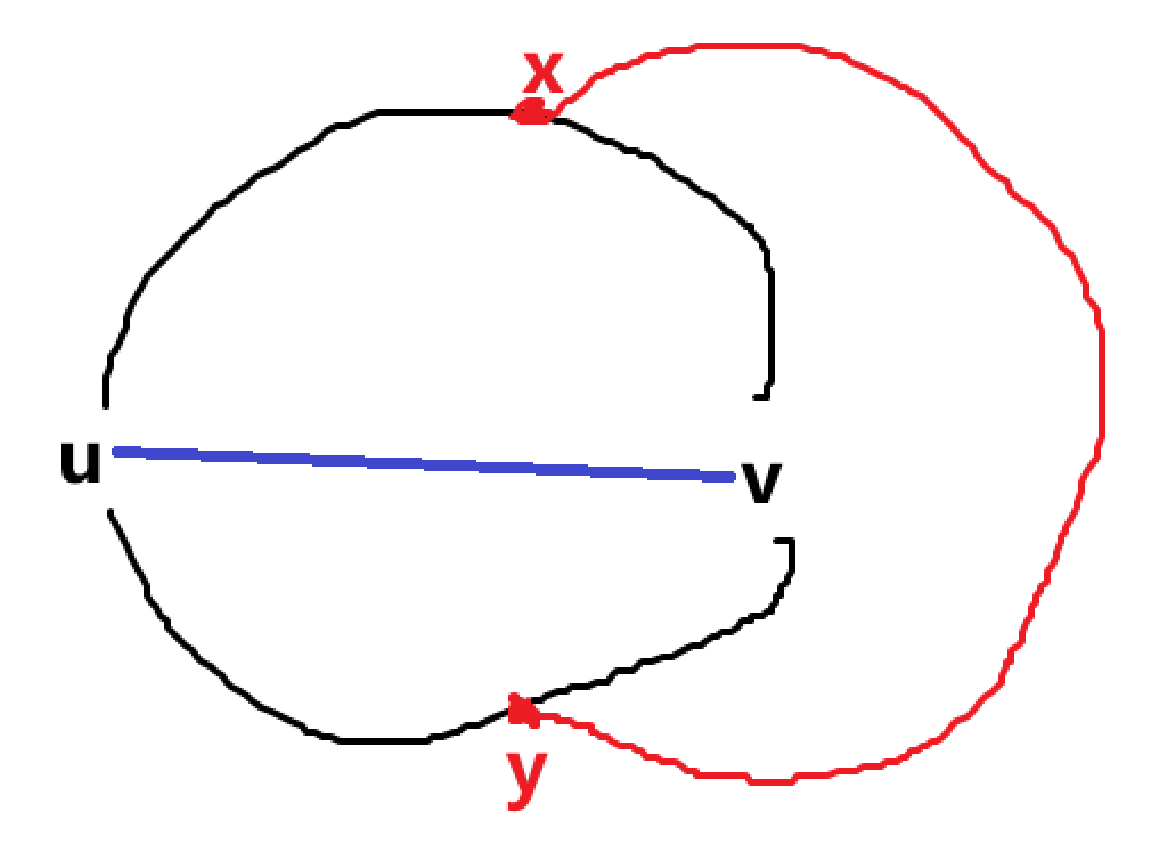
现在我们考虑这条交叉的边，假设其端点是 \(s,t\)（可以和已有点重合），记 \(C_x:u\to x\to v-u\)，也就是上半环和蓝边构成的环（类似地，下半环记为 \(C_y\)）。

根据 \(\text{Lemma }1\)，不可能有 \(s,t\in p_x\) 或 \(s,t\in p_y\)。

然后下图的情况是不行的

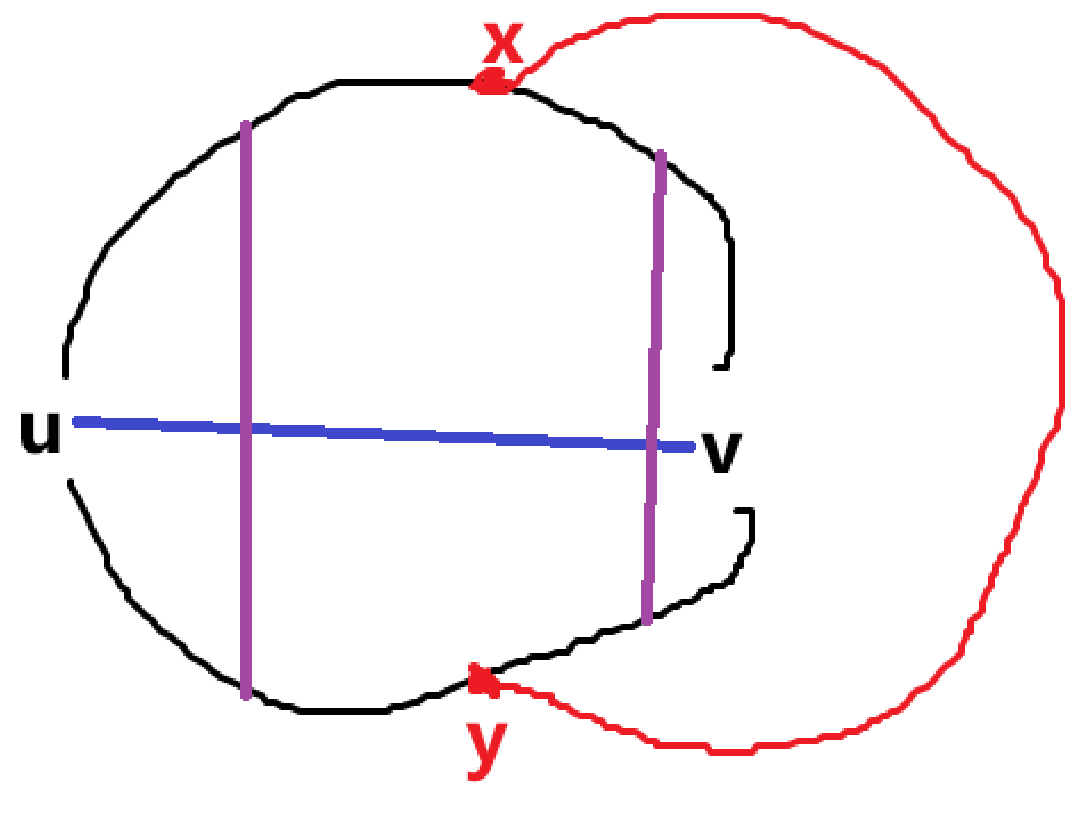
因为我们可以把紫色边放到外面去且不破坏可平面性。

此时一个 \(\text{naive}\) 的构造就是图中绿边

此时我们观察 \(u,v,s,t,x,y\) 构成的子图（路径视为边），把其分成 \(\{v,y,s\}\) 和 \(\{u,x,t\}\) 两部分，不难发现其与 \(K_{3,3}\) 同胚。

然后可以想到，\(s,t\) 不一定要在环 \(C\) 上，而是可以在已经有的边上。根据 \(\text{Lemma }2\)，这里已经有的边是不包括 \(x\to y\) 的（图中红边）。

不失一般性，先讨论有一个点在环上的情形，此时设 \(s\in C,t\not\in C\) 的情形。

根据对称性，可以设 \(s\in u\to x\)，因为首先 \(C_x\) 和 \(C_y\) 是对称的，我们可以把 \(s\) 放到 \(C_x\) 上，然后红边其实可以从右边穿过，也可以从左边穿过，所以 \(u\to x\) 和 \(v\to x\) 也是对称的。并且显然的，\(s\ne u\land s\ne v\)。

首先，我们看 \(s\ne x\) 的情况。

这个时候 \(t\) 是在 \(C\) 内部的，而 \(t\) 如果移动到 \(C_x\) 内部，\(s-t\) 和 \(u-v\) 就不交叉了，这说明还有一条边约束 \(t\) 必须在 \(C_y\) 内部。这条“约束边”无非就 \(5\) 种情况，如下图中紫色边：

直接描述太抽象了，我们设 \(e_1:t-u\)，然后按逆时针方向转一圈依次是 \(e_2,e_3,e_4,e_5\)。其中 \(e_3:t-y,e_5:t-v\)，\(e_2\) 在 \(e_1,e_3\) 之间，\(e_4\) 在 \(e_3,e_5\) 之间。

这里我们没有约束 \(e_2,e_4\) 是具体的某条边，所以其实可能有多条这样的边。

然后我们说过，\(G\) 是 \(3-\)连通的，于是 \(t\) 必须有 \(3\) 条到 \(C\) 的路径。不失一般性，我们可以让其中两条属于 \(e_i,i\in\{1,2,3,4,5\}\)，否则在 \(C_y\) 中有一条路径，在 \(C_x\) 中有两条路径，这时根据对称性，我们把 \(s-t\) 视为在 \(C_y\) 中的那条。

然后有 \(e_2\) 或者 \(e_4\) 的话，我们把其到 \(u/y/v\) 视为一条路径是同胚的（通过加边），如果 \(e_2,e_4\) 有两条，那么保证这个转化没有交叉即可。然后这个转化还有一个细节就是不要转化出 \(u-t-v\) 的路径就好。本质上就只有 \(e_1,e_3\) 和 \(e_3,e_5\) 两种情况。

也就是下图中的两种

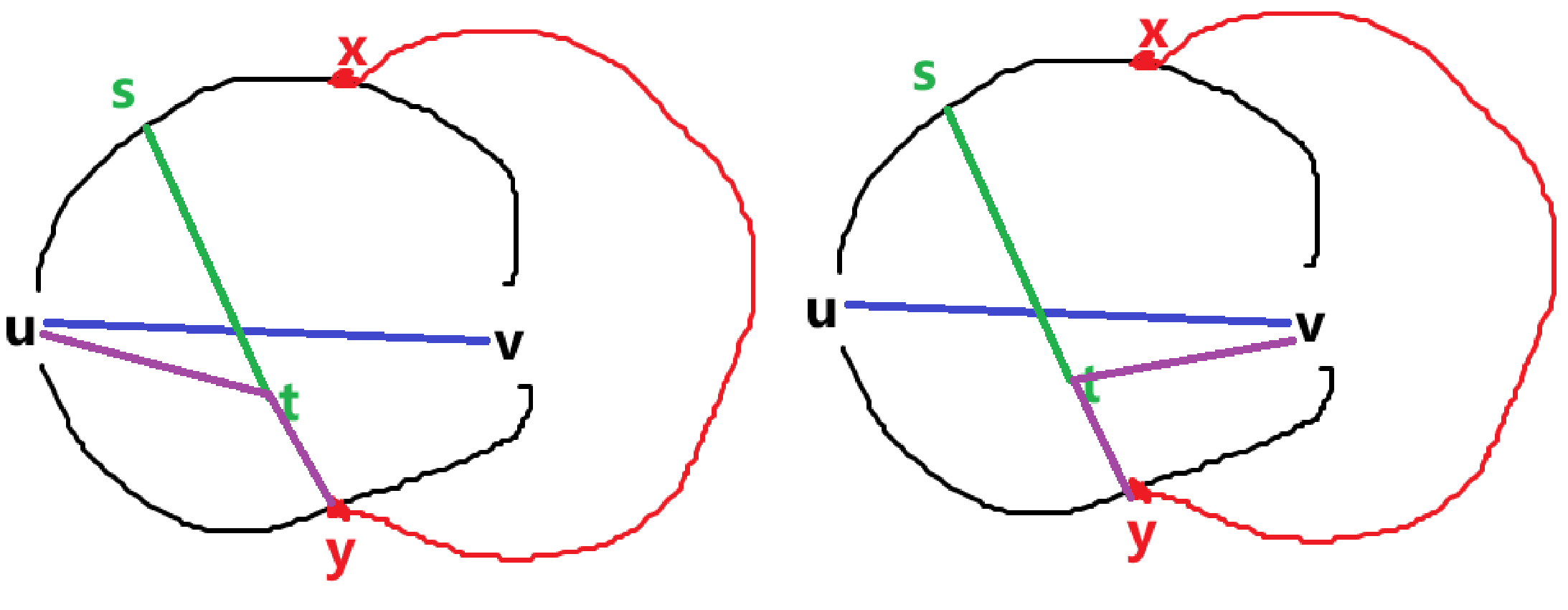
左图中 \(\{v,x,t\}\) 和 \(\{u,y,s\}\) 构成一个和 \(K_{3,3}\) 同胚的子图，右图中 \(\{u,x,t\}\) 和 \(\{v,y,s\}\) 构成一个和 \(K_{3,3}\) 同胚的子图。

接着考虑 \(s=x\) 的情况。

和上面的规约一样，如果 \(t\) 和 \(u\to y\to v\) 上不同于 \(y\) 的一点连接，于 \(t\) 和 \(y\) 连接本质相同。而此时还需要和 \(t-u\) 和 \(t-v\) 路径本质一样的两条路径，否则像图中 \(t,T\) 一样

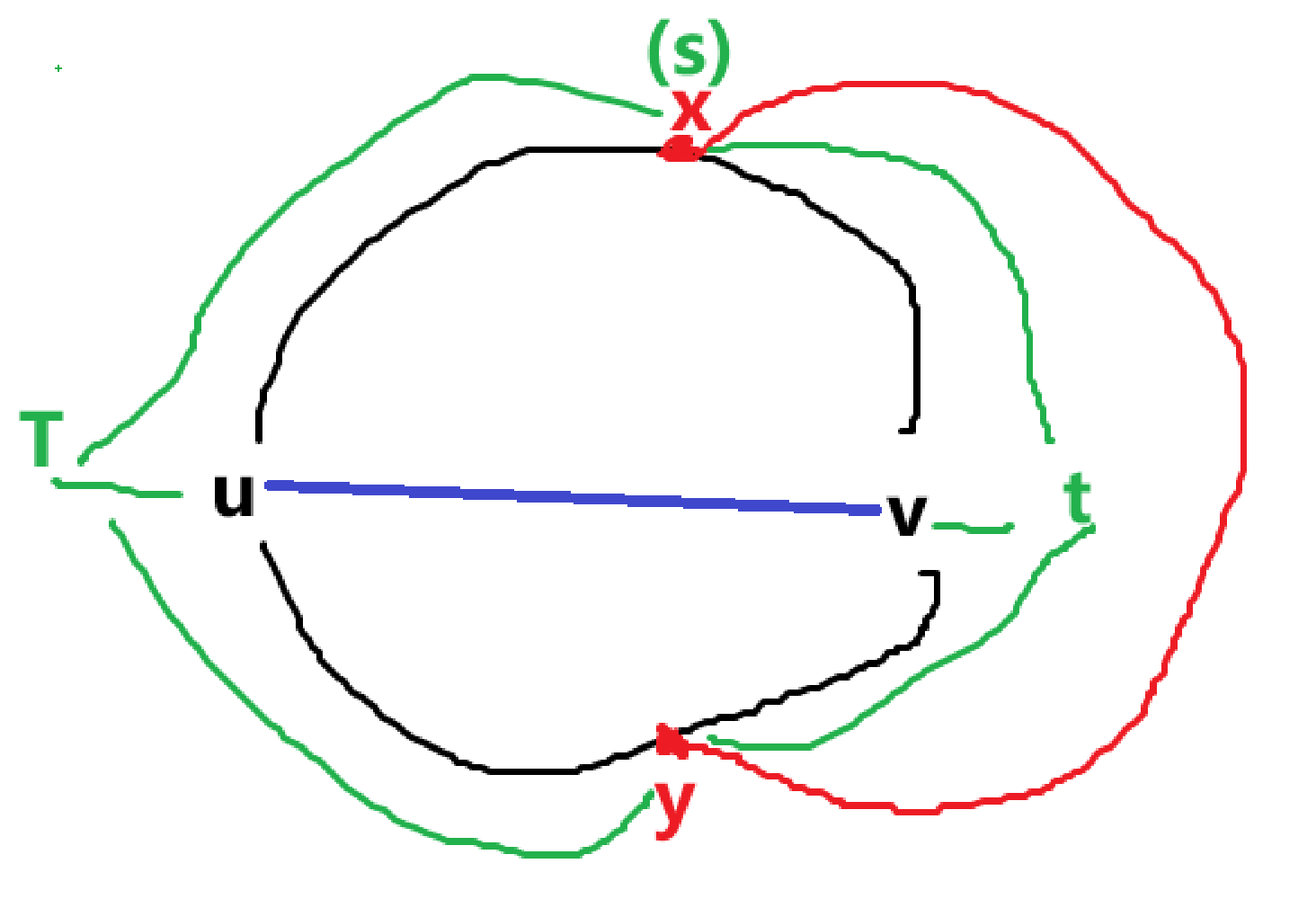
那么我们可以知道一定有和下面同胚的子图（注意图中紫色边都是转化过的）

这时可以发现 \(\{u,v,s,t,y\}\) 构成的子图和 \(K_5\) 同胚。

最后，我们考虑 \(s,t\) 都不在 \(C\) 上的情形。有上面的铺垫，我们容易想到我们需要额外的边约束 \(s,t\) 一个在 \(C_x\) 内，一个在 \(C_y\) 内。

以 \(C_x\) 为例，那就是 \(s-u,s-x\) 或者 \(s-v,s-x\) 需要同时存在（注意还要保持 \(3-\)连通，这里的边也都是路径转化而来的）

然后注意到两者不能被同一侧的 \(u/v\) 约束，否则会出现下图的情况，还是可平面的

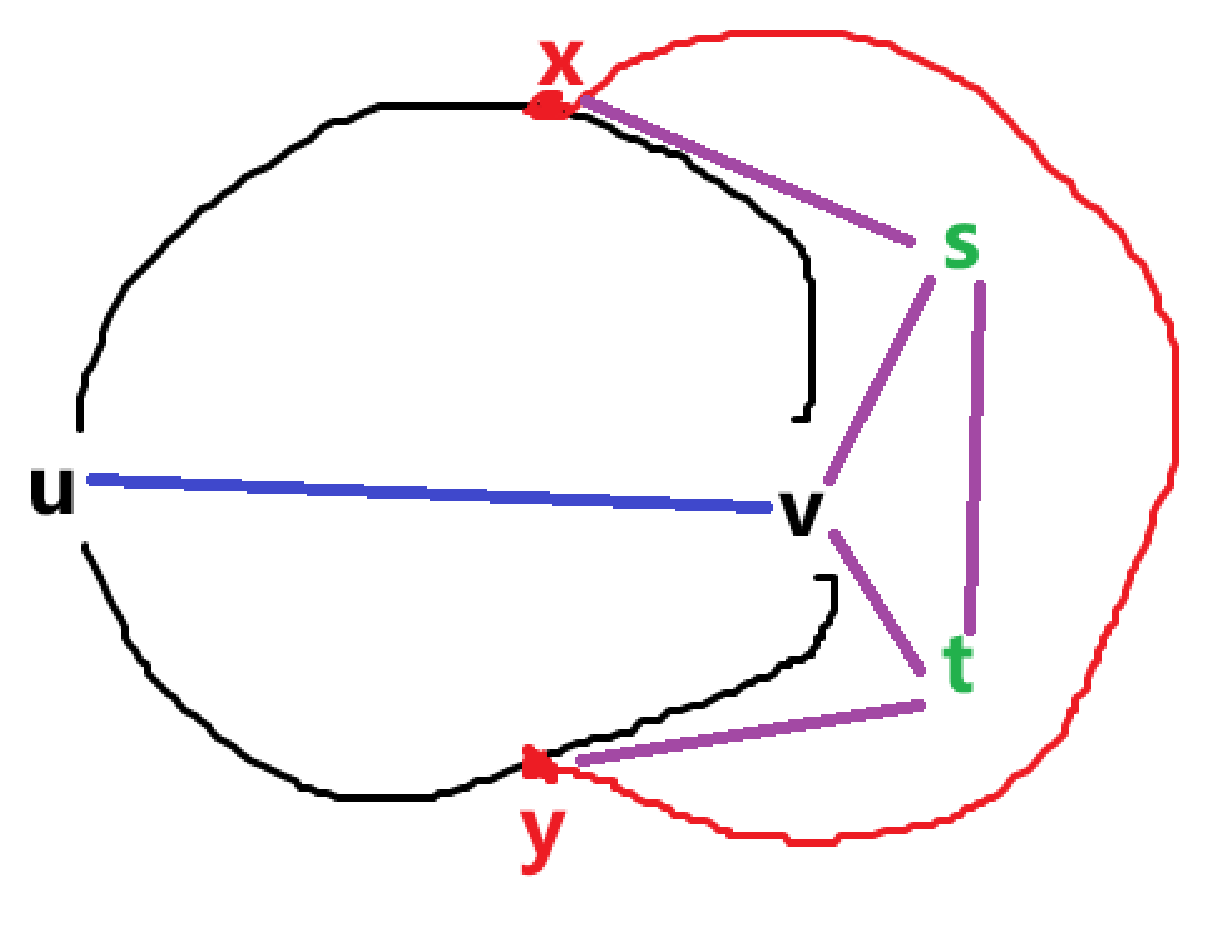
所以只能是一个被 \(u\) 约束，一个被 \(v\) 约束，也就是下图的情况

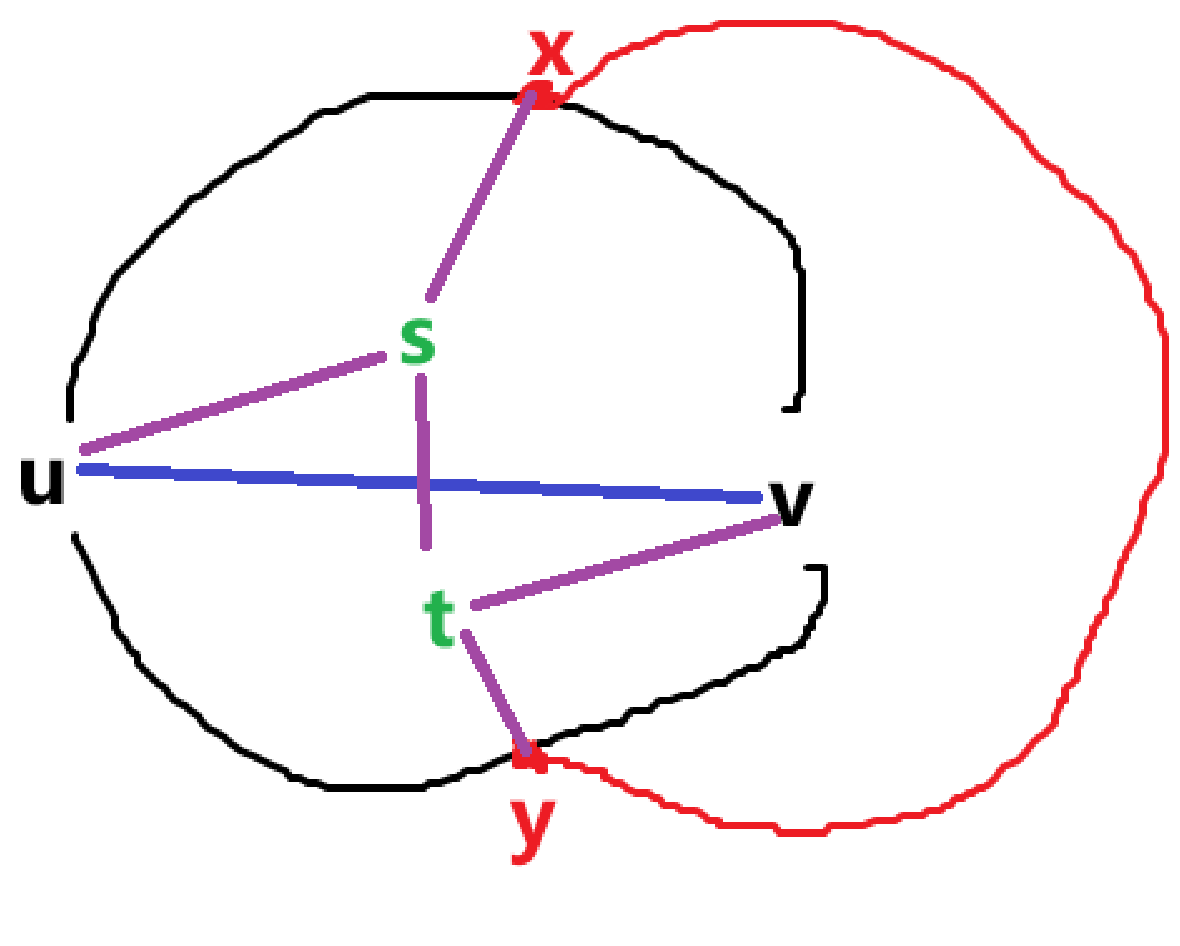
此时我们删除 \(u-x\) 和 \(v-y\)，得到的子图是和 \(K_{3,3}\) 同胚的（\(\{s,v,y\}\) 一组，\(\{t,u,x\}\) 一组）。

综上，得证。