Day2

“滚动数组”是动态规划中一种非常重要的空间优化技巧。它的核心思想是：既然计算当前这一行状态时只用到上一行的结果，那我们就没必要把之前所有行的结果都存下来。

通过滚动数组，我们可以把空间复杂度从 \(O(N \times M)\) 降低到 \(O(M)\)。

1. 为什么要“滚动”？（以 0/1 背包为例）

观察 0/1 背包的二维状态转移方程：

\[dp[i][j] = \max(dp[i-1][j], dp[i-1][j - w[i]] + v[i]) \]

你会发现，计算第 \(i\) 行的时候，永远只参考第 \(i-1\) 行。第 \(i-2, i-3 \dots\) 行的数据其实已经“没用”了。

如果我们只开两行数组：dp[2][M]，第一轮用 dp[0] 算 dp[1]，第二轮用 dp[1] 算 dp[0]，循环往复，这就是最原始的滚动数组。

2. 从“两行”进化到“一行”

实际上，我们可以更进一步，只用一个一维数组 dp[j]。

原本的逻辑是：新 dp[j] = max(旧 dp[j], 旧 dp[j - w[i]] + v[i])

如果我们直接在一个数组上操作：

for (int i = 1; i <= n; i++) {
    for (int j = m; j >= w[i]; j--) { // 注意：必须逆序
        dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
    }
}

3. 灵魂拷问：为什么一定要“逆序”？

这是滚动数组最容易出错的地方。请看下面的对比：

A. 如果是逆序（j 从 M 减小到 w[i]）：

当我们在计算 dp[j] 时，dp[j - w[i]] 还是上一轮（物品 i-1）留下的旧值。

  • 这符合 0/1 背包的定义：每个物品只选一次。
  • 这就相当于二维公式里的 dp[i-1][j - w[i]]。

B. 如果是顺序（j 从 w[i] 增加到 M）：

当我们在计算 dp[j] 时，由于 j - w[i] 比 j 小，它已经在这一轮被更新过了。

  • 如果你用更新过的 dp[j - w[i]] 来更新 dp[j]，就意味着你可能在容量更小的时候已经放过一次物品 \(i\) 了，现在又放了一次。
  • 这变成了“完全背包”（物品可以无限件使用）的解法！

4. 形象理解

想象你有一排抽屉（一维数组 dp）：

  1. 逆序更新：你从右往左改抽屉里的数。当你改右边抽屉时，你参考的是它左边还没动过的旧数。这意味着你的参考坐标还在“上一代”。
  2. 正序更新：你从左往右改。当你改右边抽屉时，左边的抽屉已经变成“这一代”的新数了。你会基于“这一代”的结果叠加，导致重复计算。

5. 针对你题目数据的对比

  • 不使用滚动数组：
    dp[3402][12880] \(\approx 43,817,760\) 个 int
    耗费内存 \(\approx\) 167 MB。（在一些限制严格的题目中会爆掉）

  • 使用滚动数组：
    dp[12880] \(\approx 12,880\) 个 int
    耗费内存 \(\approx\) 50 KB。

内存整整优化了 3000 多倍！

6. 最终的代码补全（滚动数组版）

#include<iostream>
#include<algorithm>
using namespace std;

const int MAXM = 13000;
int dp[MAXM]; // 只需要一维

void solve() {
    int n, m;
    cin >> n >> m;
    // 甚至可以边读边算，连 w[i] 和 v[i] 数组都不一定需要
    for(int i = 1; i <= n; i++) {
        int weight, value;
        cin >> weight >> value;
        // 核心：一维滚动数组逆序遍历
        for(int j = m; j >= weight; j--) {
            dp[j] = max(dp[j], dp[j - weight] + value);
        }
    }
    cout << dp[m] << endl;
}

int main() {
    solve();
    return 0;
}

总结：
滚动数组不仅是省空间，它还让代码变得更简洁。在做 DP 题目时，如果发现状态转移只和前一行（或前几项）有关，第一时间就要想到“滚动”优化。

你提供的这段代码是 标准的二维 DP 写法。它与 一维滚动数组 的核心区别主要体现在 空间维度、遍历方向、以及对“不选”情况的处理 上。

为了方便对比，我把两个版本放在一起看：

1. 核心差异对比表

特性 二维 DP (你的代码) 一维滚动数组
空间复杂度 \(O(N \times M)\)（大，易超限） \(O(M)\)（小，非常安全）
内层循环方向 正序、逆序均可 必须逆序
状态继承 需要手动写 dp[i][j] = dp[i-1][j] 自动继承（不需要写任何代码）
逻辑理解 像在填一张巨大的二维表 像在这一行格子里原地更新

2. 详细区别拆解

区别一：遍历方向的自由度

  • 二维 DP（正序）：
    在你的代码里，dp[i][j] 的值来源于 dp[i-1]（上一行）。因为数据存在不同的行里，你在填第 \(i\) 行时，无论从左往右填，还是从右往左填，都不会覆盖第 \(i-1\) 行的数据。所以方向无所谓。
  • 一维滚动（必须逆序）：
    因为只有一行，如果你从左往右填，算 f[j] 时需要的 f[j - w[i]] 可能已经被这一轮的新物品更新过了。为了拿到“上一轮”的旧数据，必须从右往左走。

区别二：“不选物品”时的处理逻辑

  • 二维 DP：
    if(j < w[i]) dp[i][j] = dp[i - 1][j];
    当背包容量装不下物品 \(i\) 时，你必须显式地把上一行的值复制到当前行。如果不写这一句，dp[i][j] 就会是默认值 0，导致结果错误。
  • 一维滚动：
    // 根本不需要写 if(j < w[i])
for(int j = m; j >= w[i]; j--) { ... }
    在一维数组里，如果 j < w[i]，循环根本不会执行。这意味着 f[j] 保持了原来的值。而原来的值恰好就是上一轮存进去的最优解。这就是所谓的“自动继承”。

区别三：内存开销（最直观的区别）

  • 二维版： 假设 \(N=3000, M=12000\)，数组大小约 \(3.6 \times 10^7\)，占内存约 144MB。
  • 滚动版： 数组大小只有 \(12000\)，占内存约 48KB。
  • 在很多题目里，144MB 可能会卡死，而 48KB 绝对稳如泰山。

3. 一个关于你代码的小修正

在你提供的这段二维代码里，有一个逻辑上的小瑕疵：

for(int j = w[i]; j <= m; j ++) { // 你这里的 j 从 w[i] 开始
    if(j < w[i]) {                // 那么这个判断永远为 false
        dp[i][j] = dp[i - 1][j];
    } else {
        dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
    }
}

问题在于： 当 j < w[i] 时（即容量装不下物品 \(i\) 时），那些更小的 j（从 \(0\) 到 \(w[i]-1\)）也应该继承上一行的值。但你的循环从 w[i] 开始，导致 dp[i][0] 到 dp[i][w[i]-1] 的值全是 0，没有继承上一行。

正确的二维写法应该是：

for(int j = 0; j <= m; j++) { // j 从 0 开始遍历所有容量
    if(j < w[i]) dp[i][j] = dp[i - 1][j]; 
    else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
}

总结

二维 DP 的优势在于逻辑最严谨、容易调试（你可以打印出整个表看哪里错了）；而滚动数组的优势在于极致的空间压缩。

在实际比赛和做题中，0/1 背包通常首选一维滚动数组，因为它更简洁，且不容易在处理 j < w[i] 的继承逻辑上出错。

二进制优化

太棒了，这正是彻底理解优化的最好方式。通过对比“笨代码”，你会瞬间发现二进制优化到底“省”在了哪里。

这就是多重背包最原始、最直观的暴力拆分法（也就是把多重背包强行当成 0/1 背包做）：

1. “笨代码”实现（暴力拆分）

这段代码逻辑是：如果你说某种宝物有 100 件，那我就写一个循环，认认真真地跑 100 次 0/1 背包的逻辑，把它当成 100 个独立的宝物去处理。

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

int dp[40005];

int main() {
    int n, W;
    cin >> n >> W;

    for (int i = 0; i < n; i++) {
        int v, w, m;
        cin >> v >> w >> m;

        // --- 笨办法开始 ---
        // 你有 m 个物品，我就老老实实循环 m 次
        // 每次循环都处理“1个”这种物品
        for (int k = 1; k <= m; k++) { 
            
            // 下面这就是纯粹的 0/1 背包逻辑
            for (int j = W; j >= w; j--) {
                dp[j] = max(dp[j], dp[j - w] + v);
            }
            
        }
        // --- 笨办法结束 ---
    }

    cout << dp[W] << endl;
    return 0;
}

2. 现在对比：优化的本质到底是什么？

请看这两个代码最核心的区别：

笨代码的逻辑：

如果要拿 8 个物品，笨代码会问你 8 次相同的问题：

  1. “多给你 1 个，你要不要？”（跑一遍 \(W\) 长度的循环）
  2. “再多给你 1 个，你要不要？”（再跑一遍 \(W\) 长度的循环）
  3. ……（重复 8 次）
    总计算量：\(8 \times W\)

二进制优化的逻辑：

它把这 8 个物品打包成了：1个、2个、4个、1个（共4捆）。它只问你 4 次问题：

  1. “这 1个 包装好的你要不要？”（跑一遍 \(W\) 长度的循环）
  2. “这 2个 包装好的你要不要？”（跑一遍 \(W\) 长度的循环）
  3. “这 4个 包装好的你要不要？”（跑一遍 \(W\) 长度的循环）
  4. “剩下的 1个 你要不要？”（跑一遍 \(W\) 长度的循环）
    总计算量：\(4 \times W\)

3. “优化”本质的终极总结

优化的本质是：合并重复决策。

  • 笨代码是在进行“步进式决策”：每次只走 1 小步（数量 +1）。
  • 二进制优化是在进行“跳跃式决策”：它利用二进制的特性，每次决策的步长是 1, 2, 4, 8... 这样成倍增长。

为什么跳着走也对？

因为 \(1, 2, 4, 8 \dots\) 这些数字就像“砝码”。

  • 如果你想拿 7 个，笨代码要考虑 7 次。
  • 二进制优化只需要考虑 1, 2, 4 这三捆。如果你这三捆都选了，刚好就是 7 个！
  • 在这个过程中，它没有漏掉任何一种可能。你想要 1 到 7 之间的任何数量，都能通过 1, 2, 4 组合出来。

结论：

二进制优化就是把原来需要做 \(m\) 次的决策，压缩成了只需要做 \(\log_2(m)\) 次决策。

  • 当 \(m=1024\) 时：
    • 笨代码要决策 1024 次。
    • 二进制优化只要决策 10 次（\(2^{10}=1024\)）。

这就是它快 100 倍的原因！ 你现在看这段笨代码，是不是觉得那个 for (int k = 1; k <= m; k++) 简直是在浪费生命？这就是优化的爽感所在。

在线还是离线？

在编写多重背包（二进制优化）时，你会发现有两种写法：一种是像你刚才那份代码一样，先拆分并存入 w1 和 v1 数组，然后再跑 DP；另一种是边拆分边跑 DP。

判断是否需要用数组来存，主要取决于以下三个维度：

1. 内存限制（最核心的判断标准）

这是最实际的考量。

  • 需要数组的情况：如果 \(N\)（物品种类）和 \(C\)（数量）都不大，内存绰绰有余，用数组存起来逻辑会非常清晰（预处理和计算分开）。
  • 不需要数组的情况：如果题目内存限制非常紧（例如只有 16MB 或 32MB），而 \(N \times \log C\) 的量级很大，那么 w1 和 v1 数组可能会导致 MLE（内存超限）。
    • 优化技巧：你可以在读入一种物品后，立刻进行二进制拆分，并在拆分出的每一个“小包裹”生成时，直接跑 0/1 背包的内层循环。这样你就省去了存放成千上万个包裹的空间。

2. 是否需要对物品进行“二次处理”

  • 需要数组的情况：如果你在跑 DP 之前，需要对所有拆分出来的物品进行排序（比如某些贪心结合 DP 的题目，或者需要按性价比排序），那么你必须先把它们全部存进数组或 vector 里。
  • 不需要数组的情况：标准的背包问题，物品的先后顺序完全不影响最终结果。这种情况下，边读入、边拆分、边计算是最省空间的做法。

3. 代码的可读性与调试需求

  • 需要数组（预处理法）：
    • 优点：逻辑解耦。第一步只管拆，第二步只管算。调试时你可以很方便地打印出 w1 清单，看看拆得对不对。
    • 缺点：多了一层空间开销。
  • 不需要数组（在线处理法）：
    • 优点：代码更紧凑，空间复杂度极低。
    • 缺点：逻辑嵌套在一起。如果结果错了，你很难一眼看出是拆分逻辑有问题还是 DP 转移逻辑有问题。

举例对比：如何把数组“减掉”？

如果你想省掉数组，可以把代码改成这样：

// 在线处理法：不使用 w1, v1 数组
for (int i = 1; i <= n; i++) {
    int v, w, c;
    cin >> v >> w >> c; // 读入一种物品
    
    // 边拆分边计算
    for (int j = 1; j <= c; j <<= 1) {
        int cur_w = j * w;
        int cur_v = j * v;
        // 直接针对这一捆跑 0/1 背包
        for (int k = m; k >= cur_w; k--) {
            dp[k] = max(dp[k], dp[k - cur_w] + cur_v);
        }
        c -= j;
    }
    
    if (c > 0) { // 处理尾巴
        int cur_w = c * w;
        int cur_v = c * v;
        for (int k = m; k >= cur_w; k--) {
            dp[k] = max(dp[k], dp[k - cur_w] + cur_v);
        }
    }
}

总结建议

  1. 初学者/普通比赛：建议用数组存。逻辑更分明，不容易写乱。现在的题目给的内存通常很大（128MB或256MB），存几万个 int 毫无压力。
  2. 高级竞赛/内存杀手题：如果内存限制在 64MB 以下，且 \(N \times \log C\) 达到 \(10^5\) 以上，请务必使用在线处理法（不存数组）。
  3. 特殊要求：只要题目不要求你给物品排序，或者不需要你回溯找出具体拿了哪些物品（路径记录），都可以不用数组存。

一句话总结：能不存就不存（省空间），除非你要排序（逻辑需要）。

Difference

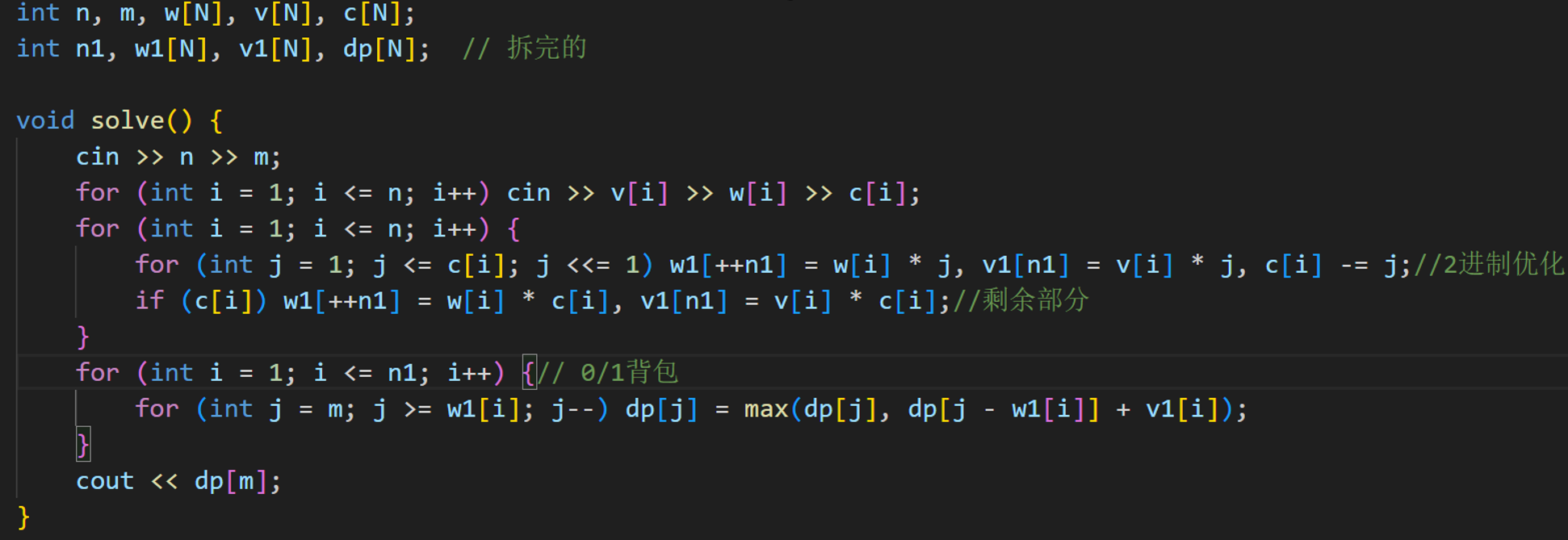
500d35a70defd10fd92d3b06b7e94b87

这是一个非常敏锐的观察！你发现了“存储处理”和“在线处理”在代码结构上的一个显著视觉差异。

其实，并不是在线处理比数组存多算了一次，而是它们的“交作业时间”不同。

我们可以用一个简单的比喻来解释：

1. 数组存（预处理法）：先打包放进仓库，最后统一搬运

逻辑：

  1. 打包阶段：你手里拿着一种物品，拆成 1 个、2 个、4 个……还有剩下的。你把这些“包裹”全部扔进两个大仓库（w1 和 v1 数组）。
    • 进仓库的动作分两步（循环里的和 if 里的），但它们只是在记账（++n1）。
  2. 搬运阶段：所有物品都拆完记好账了。你写了一个统一的循环 for(int i = 1; i <= n1; i++)。
    • 这个循环里只有一行 dp 统计代码。它不管你是“正常的 2 的幂”还是“剩下的尾巴”，反正都在 n1 这个清单里，它挨个扫一遍就行了。

结论： 数组法把“统计 dp 的代码”写在了一个远离拆分逻辑的地方，所以看起来只写了一次。

2. 在线处理：边打包边搬运，到手立刻处理

逻辑：
由于你没有 w1 和 v1 仓库来临时存放包裹，你必须“现拆现卖”。

  1. 拆出正常的包裹（循环内）：
    当你拆出一个 2 的幂（比如 4 个一捆）时，因为没有地方存，你必须立刻跑一遍 dp 统计，把它算进结果里。
  2. 拆出剩下的尾巴（if 内）：
    当循环结束，发现还剩 3 个没拆。这时候你也必须立刻再跑一遍 dp 统计。

结论： 因为你没有数组来“汇总”这些包裹，所以你每产生一个包裹（不管是循环产生的还是 if 产生的），都必须手动写一遍 dp 更新逻辑。

3. 本质原因：包裹的“出生地”有两个

不管是哪种写法，多重背包二进制拆分都会产生两种包裹：

  1. 规律包：数量是 \(1, 2, 4, 8 \dots\) 的包。
  2. 零头包：最后剩下的 \(m - (1+2+4 \dots)\) 的包。
  • 数组法：把这两类包裹都打上标签（++n1），装进同一个箱子。后面只需要一个循环对着箱子操作。
  • 在线法：这两类包裹在不同的代码块里“出生”。因为没有箱子装它们，所以你必须在它们出生的地方分别给它们安排“工作”（跑 dp）。

形象比喻：快递分拣

  • 数组法（存数组）：
    你是个分拣员。你把快递拆开，不管是大盒还是小盒，全部贴上标签放到传输带上。最后，传输带尽头的一个扫描仪（唯一的 dp 循环）扫描所有通过的盒子。

  • 在线法（不存数组）：
    你也是分拣员。但你没有传输带。
    你从左手拆出一个大盒，得赶紧跑到扫描仪那扫一下（第一次 dp 统计）；
    然后再回去拆出一个小盒，再跑过去扫一下（第二次 dp 统计）。
    因为扫描仪没法自动等你，你每拿出一个盒子，都得亲手去扫。

总结

计算总量是一模一样的。
如果你觉得在线处理写两次 dp 循环很麻烦，你可以写一个简单的小函数（比如 void update_dp(int weight, int value)），在循环里调用一次，在 if 里调用一次。这样代码看起来就整洁了！

posted @ 2026-01-23 10:24  EcSilvia  阅读(4)  评论(0)    收藏  举报