leetcode 105 从前序与中序遍历序列构造二叉树

简介

最简单的方法是使用递归来构建整棵树。

最核心的一张图

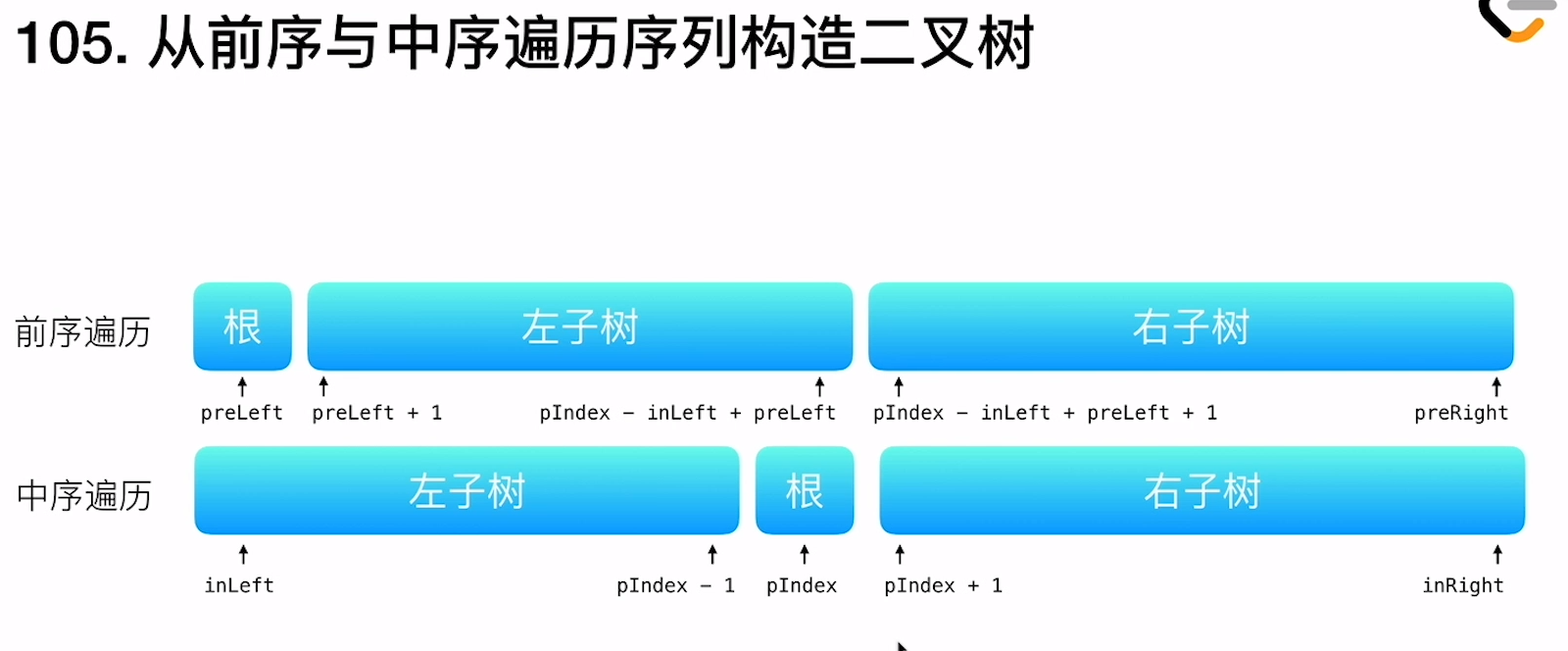
code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    unordered_map<int, int> index;
public:
    TreeNode *myBuildTree(const vector<int>&preorder, const vector<int>&inorder, int preorder_left, int preorder_right
        , int inorder_left, int inorder_right)
    {
        if(preorder_left > preorder_right){
            return nullptr;
        }
        // 前序遍历中的第一个节点就是根节点
        int preorder_root = preorder_left;
        // 再中序遍历中定位根节点
        int inorder_root = index[preorder[preorder_root]];

        // 先把根节点建立出来
        TreeNode * root = new TreeNode(preorder[preorder_root]);
        // 得到左子树中的节点数量
        int size_left_subtree= inorder_root - inorder_left;
        // 递归的构造左子树， 兵连接到根节点
        // 先序遍历中 从左边界 + 1 开始的 size_left_subtree 个元素就对应了中序遍历中， 从左边界开始到根节点的个数
        root->left = myBuildTree(preorder, inorder, preorder_left + 1, preorder_left + size_left_subtree,  inorder_left, inorder_root - 1);
        // 递归地构造右字数， 并连接到根节点
        root->right = myBuildTree(preorder, inorder, preorder_left + size_left_subtree + 1, preorder_right,  inorder_root + 1, inorder_right);
        return root;

    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int n = preorder.size();
        for(int i=0; i<preorder.size(); i++){
            index[inorder[i]] = i;
        }
        return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1);
    }
};

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    Map<Integer, Integer> index;
    public Solution(){
        index = new HashMap<Integer, Integer>();
    }
    public TreeNode myBuildTree(int [] preorder, int [] inorder, int preorder_left, int preorder_right, int inorder_left, int 
    inorder_right) 
    {
        if(preorder_left > preorder_right || inorder_left > inorder_right) {
            return null;
        }
        // 前序遍历中的第一个节点就是根节点
        int preorder_root = preorder_left;
        int inorder_root = index.get(preorder[preorder_root]);
        TreeNode root = new TreeNode(preorder[preorder_root]);
        int inorder_sub = inorder_root - inorder_left;
        root.left = myBuildTree(preorder, inorder, preorder_left + 1, preorder_left + inorder_sub, inorder_left, inorder_root - 1);
        root.right = myBuildTree(preorder, inorder, preorder_left + inorder_sub + 1, preorder_right, inorder_root + 1, inorder_right);
        return root;
    }
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        for(int i=0; i<preorder.length; i++){
            index.put(inorder[i], i);
        }
        return myBuildTree(preorder, inorder, 0, preorder.length - 1, 0, inorder.length - 1);
    }
}