线性表

github仓库：https://github.com/EanoJiang/Datastructures-and-algorithms

线性表

n个相同数据类型的数据元素构成的优先序列

n=0的时候为空表

1742523654326

案例1:图书管理系统

1742524297066

#include <stdio.h>
#include <string.h>

typedef struct {
    int isbn;
    char bookName[20];
    double price;
}book;

void main(){
    book *book_1;
    book_1->isbn = 123456;
    strcpy(book_1->bookName, "C程序设计");//数组赋值函数
    book_1->price = 20.0;
}

顺序表(数组)

逻辑上相邻，存储空间连续

初始化

#include <stdio.h>
#include <stdlib.h>

#define MAXSIZE 100
typedef int ElemType;

typedef struct {
    ElemType data[MAXSIZE];
    int length;
}SeqList;

/*顺序表——初始化*/
void initList(SeqList *L){
    L->length = 0;
}

int main(){
    SeqList list;
    initList(&list);
    printf("初始化成功\n");
    printf("length = %d\n", list.length);
    printf("占用字节数 %zu\n", sizeof(list.data));

    return 0;
}

/*如果要用指针，需要malloc分配内存*/
// int main(){
//     SeqList *list = (SeqList *)malloc(sizeof(SeqList)); // 为list分配内存
//     if (list == NULL) {
//         printf("内存分配失败\n");
//         return 1; // 如果内存分配失败，返回非零值表示错误
//     }
//     initList(list);
//     printf("初始化成功\n");
//     printf("length = %d\n", list->length);
//     printf("占用字节数 %zu\n", sizeof(list->data));
//     free(list); // 释放内存
//     return 0;
// }

声明list ，则对应 list->参数*

声明 list ，则对应 list.参数

在尾部添加元素

/*顺序表——添加元素到末尾*/
int appendElem(SeqList *L, ElemType new){
    if(L->length >= MAXSIZE){
        printf("列表已满\n");
        return -1;
    }
    //将元素添加到末尾
    L->data[L->length] = new;
    //更新length
    L->length++;
    return 1;
}

遍历顺序表

/*顺序表——遍历打印*/
void listElem(SeqList *L){
    for(int i = 0; i < L->length; i++){
        printf("%d ",L->data[i]);
    }
    printf("\n");
}

int main(){
    SeqList list;

    initList(&list);
    printf("初始化成功\n");
    printf("length = %d\n", list.length);
    printf("占用字节数 %zu\n", sizeof(list.data));
    printf("\n");

    appendElem(&list, 1);
    appendElem(&list, 2);
    appendElem(&list, 3);

    listElem(&list);

    return 0;
}

插入元素

/*顺序表——插入元素*/
//后面的元素都向后移动一位
void insertElem(SeqList *L, int target_index, ElemType new){
    if(L->length >= MAXSIZE){
        printf("列表已满\n");
        return;
    }
    if(target_index < 0 || target_index > L->length){
        printf("插入位置不合法\n");
        return;
    }
  
    if(target_index <= L->length){
        for(int i = L->length - 1; i >= target_index; i--){
            L->data[i+1] = L->data[i];
        }
        L->data[target_index] = new;
        L->length++;
    }
}

int main(){
    SeqList list;

    initList(&list);
    printf("初始化成功\n");
    printf("length = %d\n", list.length);
    printf("占用字节数 %zu\n", sizeof(list.data));
    printf("\n");

    appendElem(&list, 1);
    appendElem(&list, 2);
    appendElem(&list, 3);
  
    listElem(&list);

    insertElem(&list, 2, 99);
    listElem(&list);
    return 0;
}

顺序表插入数据的

最佳时间复杂度：1（在尾部插入）

最差时间复杂度：n（在头部插入）

平均：n/2

删除元素

/*顺序表——删除元素*/
//后面的元素都向前移动一位
int deleteElem(SeqList *L, int target_index,ElemType *del){
    //是否合法省略...

    //指针写入删除的元素
    *del = L->data[target_index];

    if(target_index <= L->length){
        for(int i = target_index; i < L->length; i++){
            L->data[i] = L->data[i+1];
        }
        L->length--;
    }
    return 1;
}

int main(){
    SeqList list;

    initList(&list);
    printf("初始化成功\n");
    printf("length = %d\n", list.length);
    printf("占用字节数 %zu\n", sizeof(list.data));
    printf("\n");

    appendElem(&list, 1);
    appendElem(&list, 2);
    appendElem(&list, 3);
  
    listElem(&list);

    insertElem(&list, 2, 99);
    listElem(&list);

    ElemType delData;
    deleteElem(&list, 2, &delData);
    printf("删除元素:%d\n", delData);
    listElem(&list);
    return 0;
}

查找

/*顺序表——查找*/
int findElem(SeqList *L, ElemType target){
    for(int i = 0; i < L->length; i++){
        if(L->data[i] == target){
            return i;
        }
    }
    return 0;
}

int main(){
    //这里创建的是数组（顺序表），所以下面要传入数组的地址
    SeqList list;

    initList(&list);
    printf("初始化成功\n");
    printf("length = %d\n", list.length);
    printf("占用字节数 %zu\n", sizeof(list.data));
    printf("\n");

    appendElem(&list, 1);
    appendElem(&list, 2);
    appendElem(&list, 3);
  
    listElem(&list);

    insertElem(&list, 2, 99);
    listElem(&list);

    ElemType delData;
    deleteElem(&list, 2, &delData);
    printf("删除元素:%d\n", delData);
    listElem(&list);

    printf("查找元素的index: %d\n",findElem(&list, 2));

    return 0;
}

动态分配内存地址

/*顺序表——动态分配内存地址初始化*/
typedef struct {
    ElemType *data;
    int length;
}SeqList;

SeqList *initList(SeqList *L){
    L = (SeqList *)malloc(sizeof(SeqList));
    L->data = (ElemType *)malloc(sizeof(ElemType)*MAXSIZE); // 为L分配内存
    L->length = 0;
    return L;
}

//其他功能函数都不用改

int main(){
    //创建的是一个指针，需要在声明的时候立刻分配内存
    SeqList *list = initList(list);
  
    printf("初始化成功\n");
    printf("length = %d\n", list->length);
    printf("占用字节数 %zu\n", sizeof(list->data));
    printf("\n");

    appendElem(list, 1);
    appendElem(list, 2);
    appendElem(list, 3);
  
    listElem(list);

    insertElem(list, 2, 99);
    listElem(list);

    ElemType delData;
    deleteElem(list, 2, &delData);
    printf("删除元素:%d\n", delData);
    listElem(list);

    printf("查找元素的index: %d\n",findElem(list, 2));

    //记得释放内存
    free(list->data);
    free(list);
  
    return 0;
}

总结：

线性表的特点

易查找，但是增删改麻烦(每次都要移动，时间复杂度高)

链表

存储结构特点：存储单元不一定连续

每个节点node包括数据域data和指针域*next

next 存的是下一个节点的地址

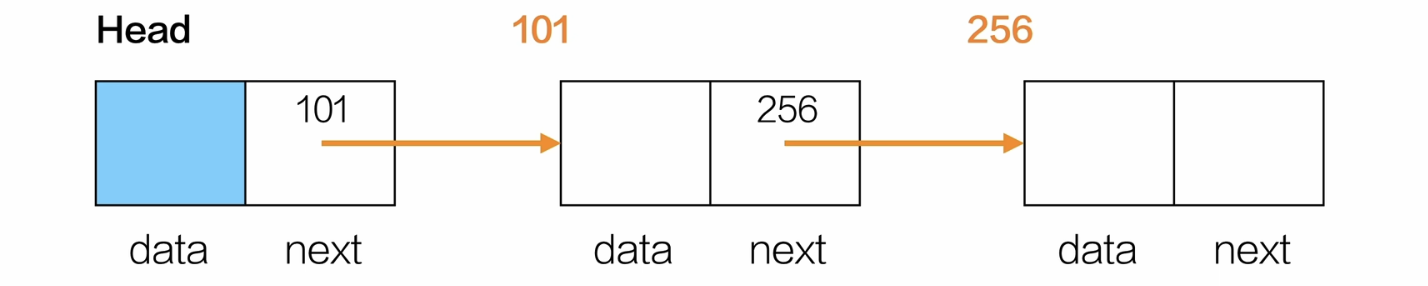
1742570944431

typedef int ElemType;

typedef struct node {
    ElemType data;
    struct node *next;
}Node;

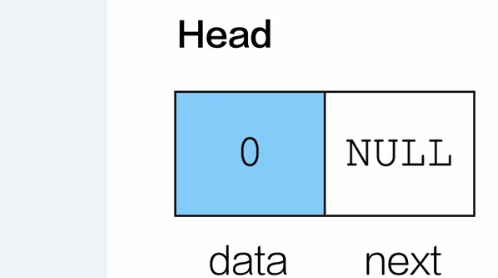
初始化

/*单链表——初始化*/
Node* initList(){
    Node *head = (Node*)malloc(sizeof(Node));
    head->data = 0;
    head->next = NULL;
    return head;//返回头节点指针，头节点可以代表整个链表
}

int main(){
    Node *list = initList();

    return 1;
}

1742576632730

插入节点——头插法

/*单链表——插入元素*/
//L: 链表头节点 ，elem: 插入元素
void insertHead(Node *L,ElemType elem){
    Node *tmp = (Node*)malloc(sizeof(Node));
    tmp->data = elem;
    tmp->next = L->next;
    L->next = tmp;
}

1742577332737

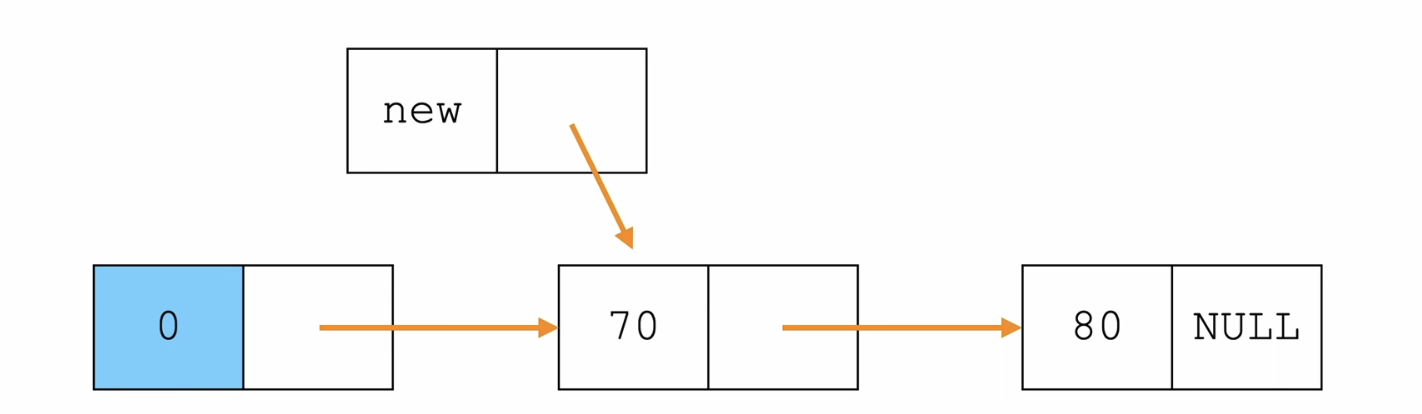
1742577318413

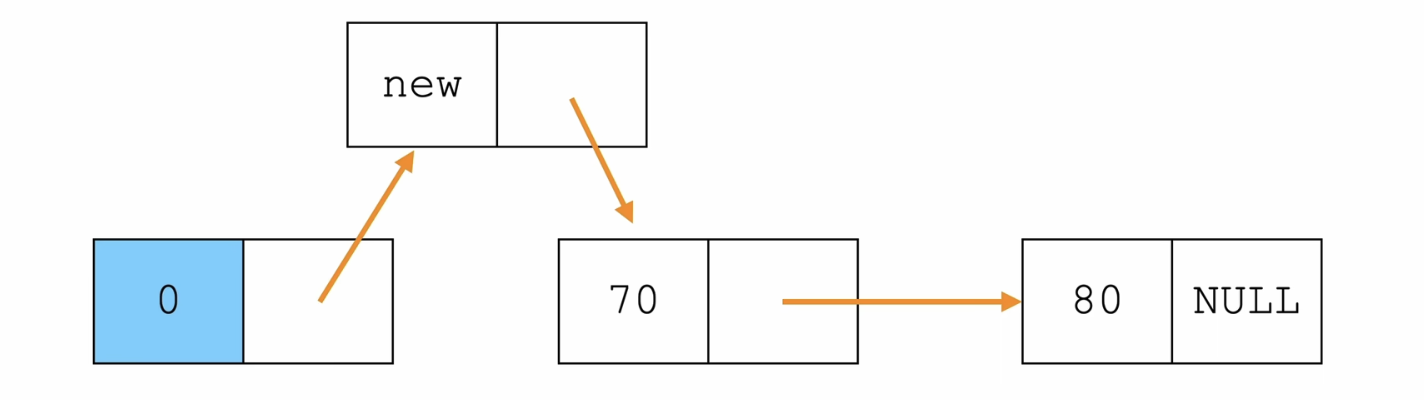
1742577345396

伪代码：

tmp.data = elem

tmp.next = head.next

head.next = tmp

详解：

先创建一个新节点，给这个新节点的data赋值
让这个新节点的next指向原来头节点的下一个节点(这一步相当于复制了一个头节点作为分支，只是这个分支的data是新的)
最后让原来头节点的next指向这个新节点(完成连接)

这里就体现出链表的插入元素效率比顺序表更高

遍历

/*单链表——遍历*/
void listNode(Node *L){
    Node *tmp = L->next;
    while(tmp!= NULL){
        printf("%d ",tmp->data);
        //更新为下一个节点
        tmp = tmp->next;
    }
    printf("\n");
}

int main(){
    Node *list = initList();
    insertHead(list,1);
    insertHead(list,2);
    insertHead(list,3);
    listNode(list);

    return 0;
}

特点：头插法的数据是和排列顺序相反的

每次都是头插，也就是先插的排在后面。

尾插法

/*单链表——尾插法*/
Node* getTail(Node *L){
    Node *tmp = L;
    while(tmp->next!= NULL){
        tmp = tmp->next;
    }
    return tmp;
}
Node* insertTail(Node *tail,ElemType elem){
    Node *tmp = (Node*)malloc(sizeof(Node));
    tmp->data = elem;
    //尾节点的next指向新节点，新节点的next指向NULL(这时候的尾节点就是新节点)
    tail->next = tmp;
    tmp->next = NULL;

    //返回新的尾节点
    return tmp;
}

int main(){
    Node *list = initList();
    insertHead(list,1);
    insertHead(list,2);
    insertHead(list,3);
    listNode(list);

    //这样写只在第一次得到尾指针时调用一次getTail()
    //后面的尾指针均由insertTail()返回值传递
    Node *tail = getTail(list);
    tail = insertTail(tail,4);
    tail = insertTail(tail,5);
    tail = insertTail(tail,6);
    listNode(list);

    return 0;
}

功能函数之间最好不要嵌套，不然耦合性太高

所以我在insertTail()里面声明tail这个参数，但是不调用getTail()获取，这样时间复杂度下降同时也解耦合。

1742579712399

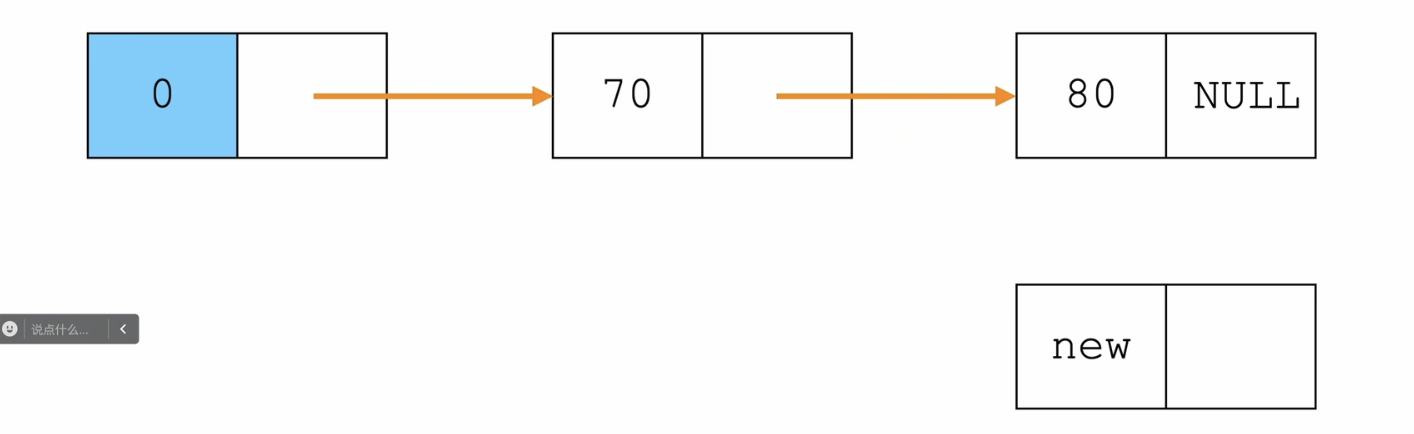
1742579728623

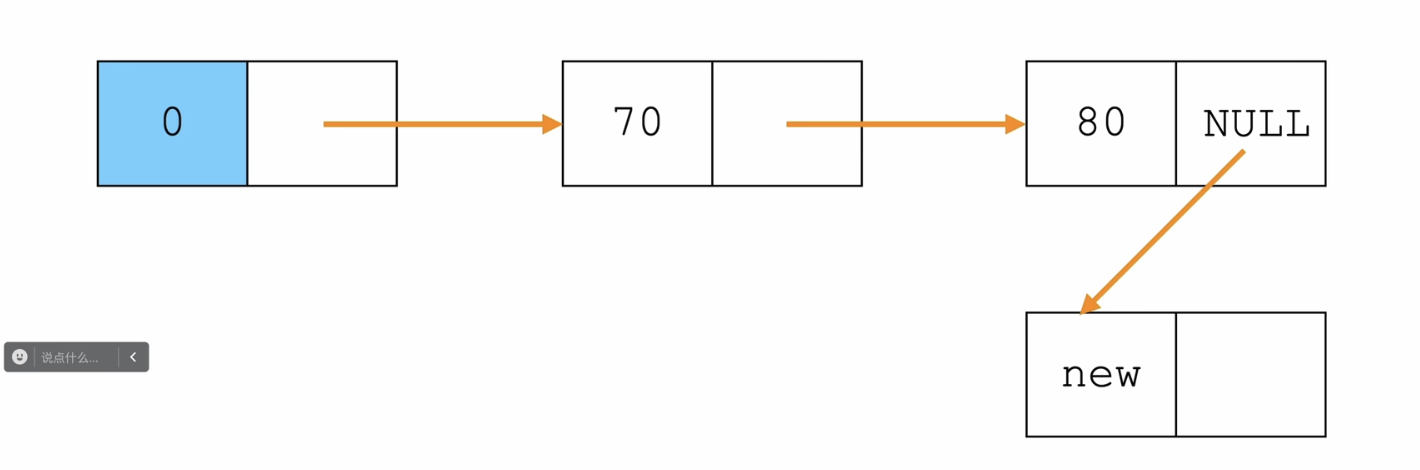
1742579739480

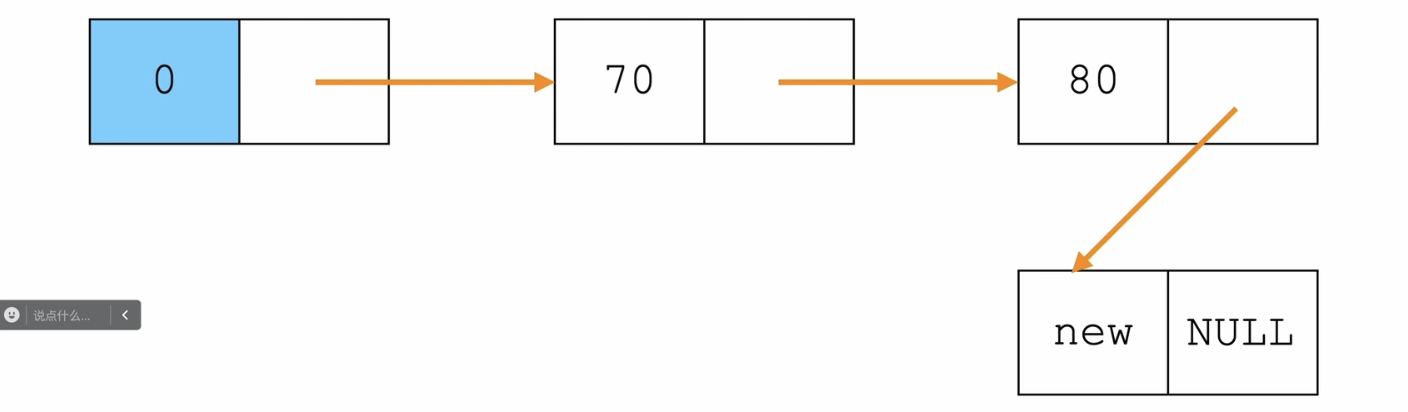
1742579768047

伪代码：

tmp.data = elem

tail.next = tmp

tmp.next = NULL

详解：

遍历找到尾节点
创建一个新节点，给这个新节点的data赋值
让尾节点的next指向新节点
最后让新节点的next指向NULL，新节点成为最终的尾节点

在指定位置插入数据

/*单链表——在指定位置插入元素*/
int insertNode(Node *L,int target_index,ElemType elem){
    //找到索引为target_index-1的节点
    Node *tmp = L;
    for(int i = 0; i <= target_index-1; i++){
        tmp = tmp->next;
        if(tmp == NULL){
            return 0;
        }
    }
    //这时tmp就是索引为target_index-1的节点
    //下面用头插法让新节点插到tmp的后面

    Node *newNode = (Node*)malloc(sizeof(Node));
    newNode->data = elem;
    newNode->next = tmp->next;
    tmp->next = newNode;

    return 1;  
}

int main(){
    Node *list = initList();
    insertHead(list,1);
    insertHead(list,2);
    insertHead(list,3);
    listNode(list);

    //这样写只在第一次得到尾指针时调用一次getTail()
    //后面的尾指针均由insertTail()返回值传递
    Node *tail = getTail(list);
    tail = insertTail(tail,4);
    tail = insertTail(tail,5);
    tail = insertTail(tail,6);
    listNode(list);

    insertNode(list,2,99);
    listNode(list);
    return 0;
}

思路：

先遍历找到索引为target_index-1的节点tmp
创建一个新节点newNode，赋值data为elem
让新节点的next和tmp的next一样，都指向tmp的下一个节点，也就是索引为target_index的节点
让tmp的next指向新节点

步骤1是尾插法的遍历找到尾节点的思路，步骤2,3,4实际上就是头插法

删除节点

/*单链表——删除指定元素*/
int deleteNode(Node *L,int target_index){
    //遍历找到要删除节点的前驱节点tmp
    Node *tmp = L;
    for(int i = 0;i <= target_index-1;i++){
        tmp = tmp->next;
        if(tmp == NULL){
            printf("要删除的节点不存在\n");
            return 0;
        }
    }

    if(target_index < 0 || 
        tmp->next == NULL){
        printf("要删除的节点索引不合法\n");
        return 0;
    }

    //delNode用来存放要删除的节点
    Node *delNode = tmp->next;

    //直接让tmp的next指向delNode的next
    tmp->next = delNode->next;
    free(delNode);
    return 1;
}

int main(){
    Node *list = initList();
    insertHead(list,1);
    insertHead(list,2);
    insertHead(list,3);
    listNode(list);

    //这样写只在第一次得到尾指针时调用一次getTail()
    //后面的尾指针均由insertTail()返回值传递
    Node *tail = getTail(list);
    tail = insertTail(tail,4);
    tail = insertTail(tail,5);
    tail = insertTail(tail,6);
    listNode(list);

    insertNode(list,2,99);
    listNode(list);

    deleteNode(list,100);
    listNode(list);
    deleteNode(list,-1);
    listNode(list);
    deleteNode(list,2);
    listNode(list);
    return 0;
}

思路：

先遍历找到要删除节点的前驱节点tmp
创建一个节点delNode用来存放要删除的节点，也就是delNode=tmp->next
直接让tmp->next = delNode->next
释放delNode的内存

获取链表的长度

/*单链表——获取链表长度*/
int listLength(Node *L){
    Node *tmp = L;
    int len = 0;
    while(tmp != NULL){
        tmp = tmp->next;
        len++; 
    }
    return len;

}

int main(){
    Node *list = initList();
    insertHead(list,1);
    insertHead(list,2);
    insertHead(list,3);
    listNode(list);

    //这样写只在第一次得到尾指针时调用一次getTail()
    //后面的尾指针均由insertTail()返回值传递
    Node *tail = getTail(list);
    tail = insertTail(tail,4);
    tail = insertTail(tail,5);
    tail = insertTail(tail,6);
    listNode(list);

    insertNode(list,2,99);
    listNode(list);

    deleteNode(list,100);
    listNode(list);
    deleteNode(list,-1);
    listNode(list);
    deleteNode(list,2);
    listNode(list);
    printf("%d",listLength(list));
    return 0;
}

1742633068067

长度是7，因为遍历节点的时候没有打印头节点，如下图：

1742633154949

释放链表

int listRealse(Node *L){
    Node *tmp = L->next;
    Node *q;

    if(tmp == NULL){
        printf("这个链表只有头节点，不用释放\n");
        return 0;
    }
    while(tmp != NULL){
        q = tmp->next;
        free(tmp);
        //向后更新tmp
        tmp = q;
    }
    L->next = NULL;
    return 0;
}

int main(){
    Node *list = initList();
    insertHead(list,1);
    insertHead(list,2);
    insertHead(list,3);
    listNode(list);

    //这样写只在第一次得到尾指针时调用一次getTail()
    //后面的尾指针均由insertTail()返回值传递
    Node *tail = getTail(list);
    tail = insertTail(tail,4);
    tail = insertTail(tail,5);
    tail = insertTail(tail,6);
    listNode(list);

    insertNode(list,2,99);
    listNode(list);

    deleteNode(list,100);
    listNode(list);
    deleteNode(list,-1);
    listNode(list);
    deleteNode(list,2);
    listNode(list);
    printf("当前链表长度%d\n",listLength(list));

    listRealse(list);
    printf("当前链表长度%d\n",listLength(list));
    listRealse(list);
    printf("当前链表长度%d\n",listLength(list));
    return 0;
}

单链表应用

双指针法

题1

思考过程：

单指针法（时间复杂度很高）

因为是单向链表，没办法反向遍历，所以想到先遍历求出链表长度，那么倒数第k个位置的索引 = 链表长度-k-1，再遍历到这个索引，返回该索引处节点的data。

缺点：求链表长度的时候是遍历求的，这部分可以用快慢指针的方法规避掉

双指针法——快慢刀

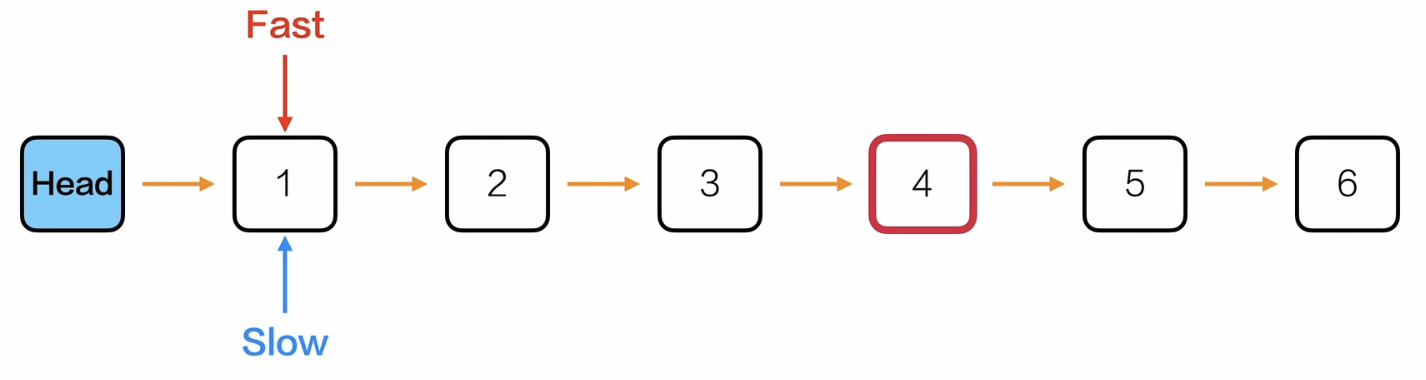
1742637190369

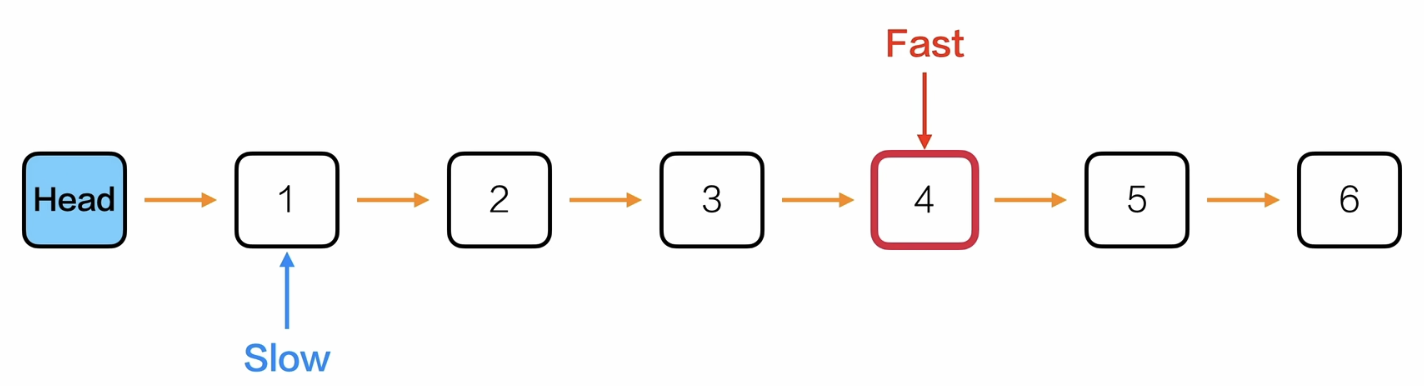
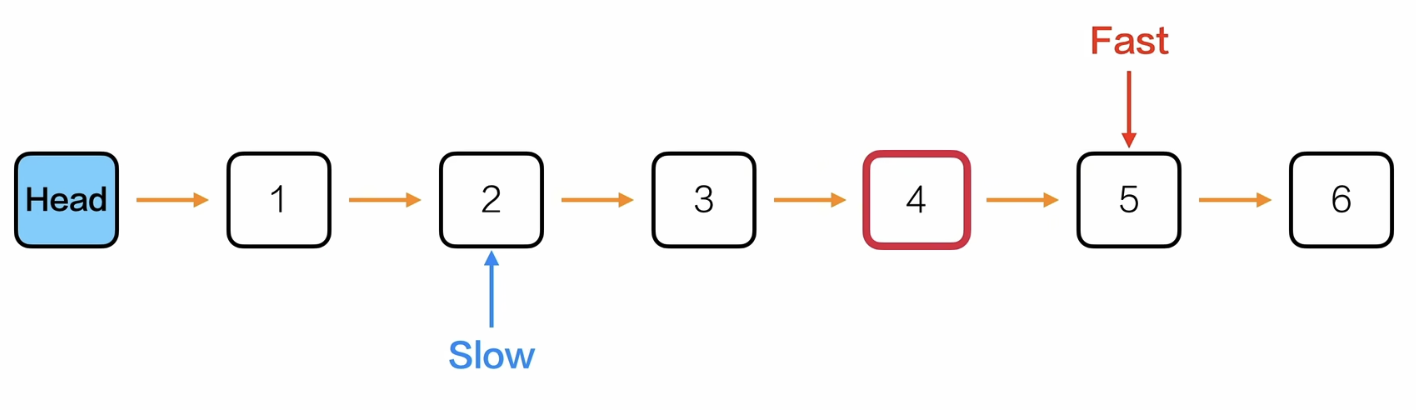
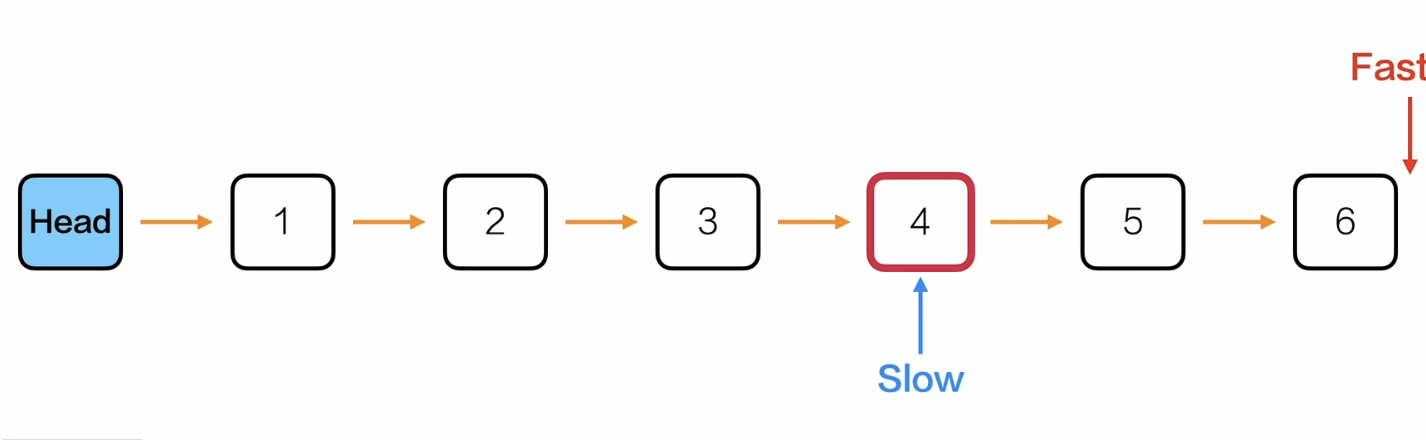
1742637487155 1742637501567 1742637516132

先让快慢指针都指向head->next
然后快指针先向后遍历k次
再让快慢指针一起向后遍历，当快指针指向NULL的时候结束，这时候慢指针就是倒数第k个位置的节点
返回慢指针->data

这样双指针法的时间复杂度 = 单指针遍历到倒数第k个位置的索引(链表长度-k-1)的循环次数 + 快指针一开始向后先走的k次

/*题目查找链表中倒数第k个位置的节点*/
//L:链表，k:倒数第k个位置
//单指针法
// ElemType listFind_1p(Node *L,int k){
//     Node *tmp = L;
//     int count = 0;
//     for(int i = 0;i <= listLength(L)-k-1;i++){
//         tmp = tmp->next;
//         count++;
//     }
//     printf("单指针法查找循环了%d次,但是计算链表总长度是遍历得到的,这部分循环次数没算进来\n",count);
//     return tmp->data;
// }
//双指针法
ElemType listFind_2p(Node *L,int k){
    Node *fast = L->next;
    Node *slow = L->next;
    int count = 0;
    //快指针先走k步
    for(int i = 0;i < k;i++){
        fast = fast->next;
    }
    //当快指针走到尾指针的时候，慢指针的位置就是倒数第k个
    while(fast != NULL){
        fast = fast->next;
        slow = slow->next;
        count++;
    }
    printf("双指针法查找循环了%d次\n",count);
    return slow->data;
}

int main(){
    Node *list = initList();
    insertHead(list,1);
    insertHead(list,2);
    insertHead(list,3);
    listNode(list);

    //这样写只在第一次得到尾指针时调用一次getTail()
    //后面的尾指针均由insertTail()返回值传递
    Node *tail = getTail(list);
    tail = insertTail(tail,4);
    tail = insertTail(tail,5);
    tail = insertTail(tail,6);
    listNode(list);

    insertNode(list,2,99);
    listNode(list);

    deleteNode(list,100);
    listNode(list);
    deleteNode(list,-1);
    listNode(list);
    deleteNode(list,2);
    listNode(list);
    printf("当前链表长度%d\n",listLength(list));

    // listRealse(list);
    // printf("当前链表长度%d\n",listLength(list));
    // listRealse(list);
    // printf("当前链表长度%d\n",listLength(list));
    for(int i = 1;i <= 10;i++){
        tail = insertTail(tail,1);
    }
    listNode(list);
    int k = 3;
    //printf("倒数第%d个节点的data是%d\n",k,listFind_1p(list,k));
    printf("倒数第%d个节点的data是%d\n",k,listFind_2p(list,k));
    return 0;
}

1742637618551

题2

//这里要改成char
typedef char ElemType;
//剩下的功能函数不变

/*题2：查找两个节点共同后缀的起始位置*/
Node* findNodeWithSuffix(Node *L1,Node *L2){
    if(L1 == NULL || L2 == NULL) return NULL;
    //获取两个链表的长度
    int len1 =  listLength(L1);
    int len2 =  listLength(L2);

    Node *fast;//快指针
    Node *slow;//慢指针
    int step; //步长：长度差值

    //让快指针指向较长链表的next
    if(len1 > len2){
        step = len1 - len2;
        fast = L1->next;
        slow = L2->next;
    }
    else{
        step = len2 - len1;
        fast = L2->next;
        slow = L1->next;
    }
    //先让快指针走step步
    for(int i = 0; i < step; i++){
        fast = fast->next;
    }
    //然后两个指针一起走，直到找到快慢指针走到同一个节点(同一个后缀的第一个字母)
    while(fast != slow){
        fast = fast->next;
        slow = slow->next;
    }
    return fast;
}

int main(){
    Node *str1 = initList();
    Node *str2 = initList();

    Node *tail1 = getTail(str1);
    Node *tail2 = getTail(str2);
    //str1的前缀是load
    tail1 = insertTail(tail1,'l');
    tail1 = insertTail(tail1,'o');
    tail1 = insertTail(tail1,'a');
    tail1 = insertTail(tail1,'d');
    //str2的前缀是be
    tail2 = insertTail(tail2,'b');
    tail2 = insertTail(tail2,'e');

    Node *suffix = initList();
    Node *tail_suffix = getTail(suffix);
    //suffix是ing
    tail_suffix = insertTail(tail_suffix,'i');
    tail_suffix = insertTail(tail_suffix,'n');
    tail_suffix = insertTail(tail_suffix,'g');

    //str1和suffix相连,也就是str1的尾节点的next指向suffix的头节点的next
    tail1->next = suffix->next;
    //str2和suffix相连
    tail2->next = suffix->next;

    listNode(str1);
    listNode(str2);
  
    printf("共同后缀的起始位置：%c\n",findNodeWithSuffix(str1,str2)->data);
    return 0;
}

思路：双指针法

标志位法

空间换时间

题3

思路：

创建一个全0数组，索引从0到最大的| data |，也就是长度为 | data |最大值 +1的数组，每个索引对应的数值是标识位，然后遍历比对链表节点的data，当链表中节点的data第一次出现时，就把这个data当作数组中的索引，令该位置的标识位为1；当后面再次出现时，如果数组索引的标识位为1，就删去链表中的这个节点。

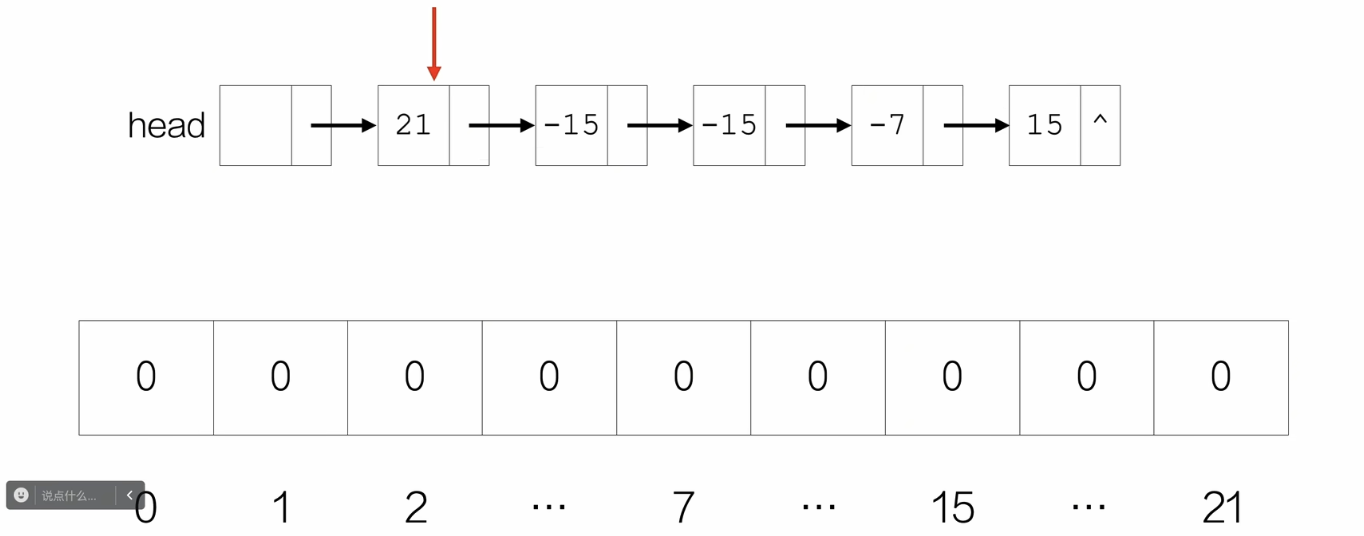
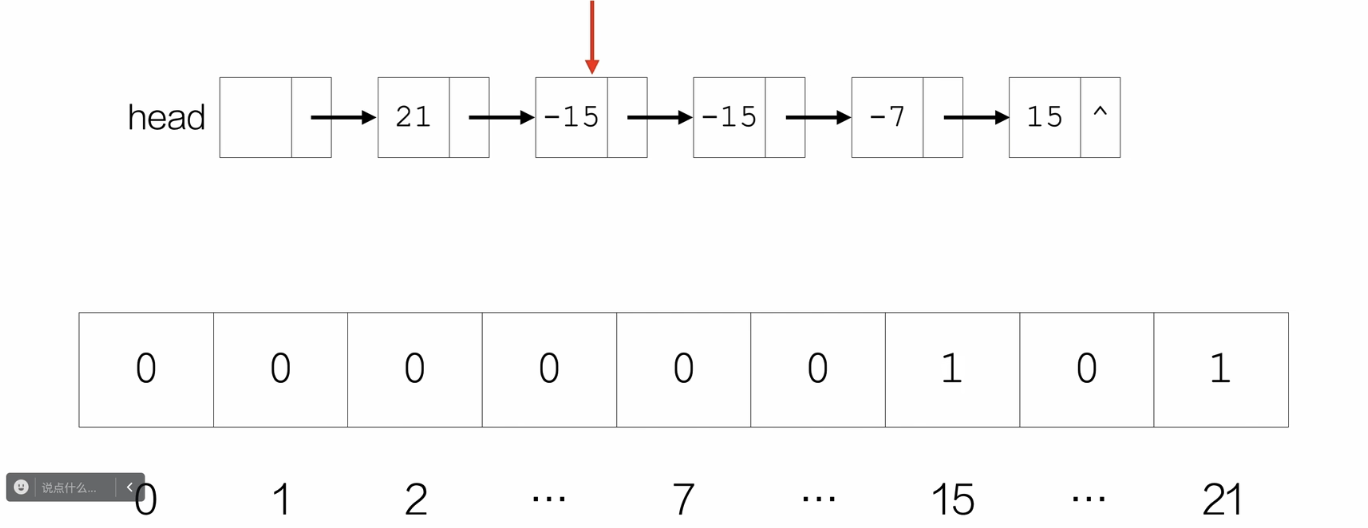
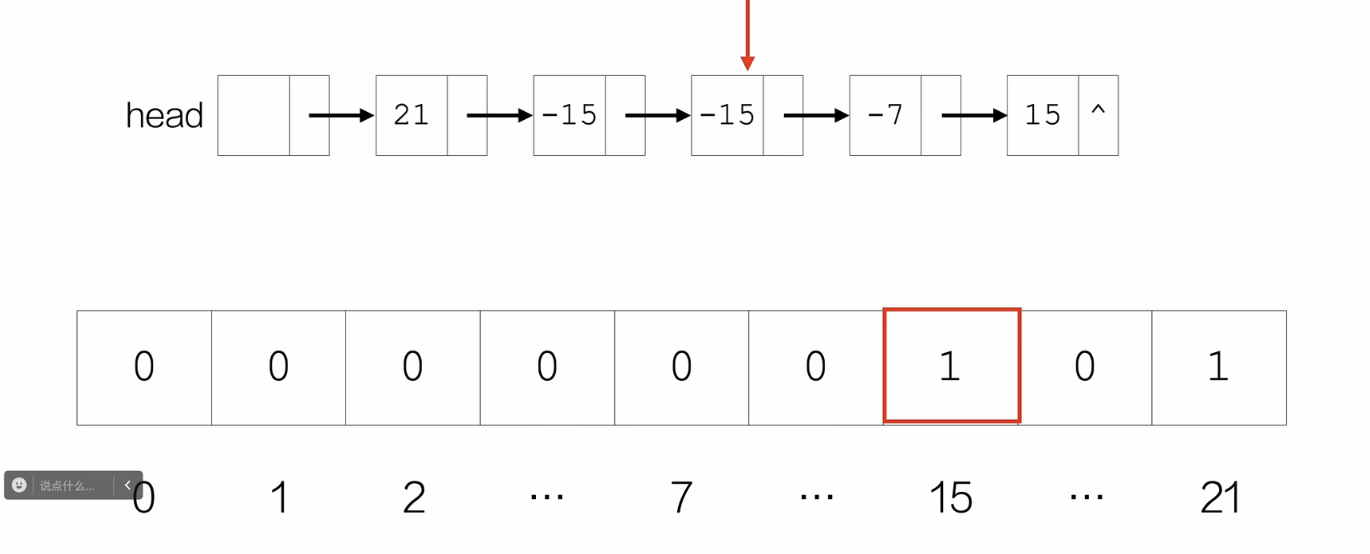
1742722293523 1742722316564 1742722331270

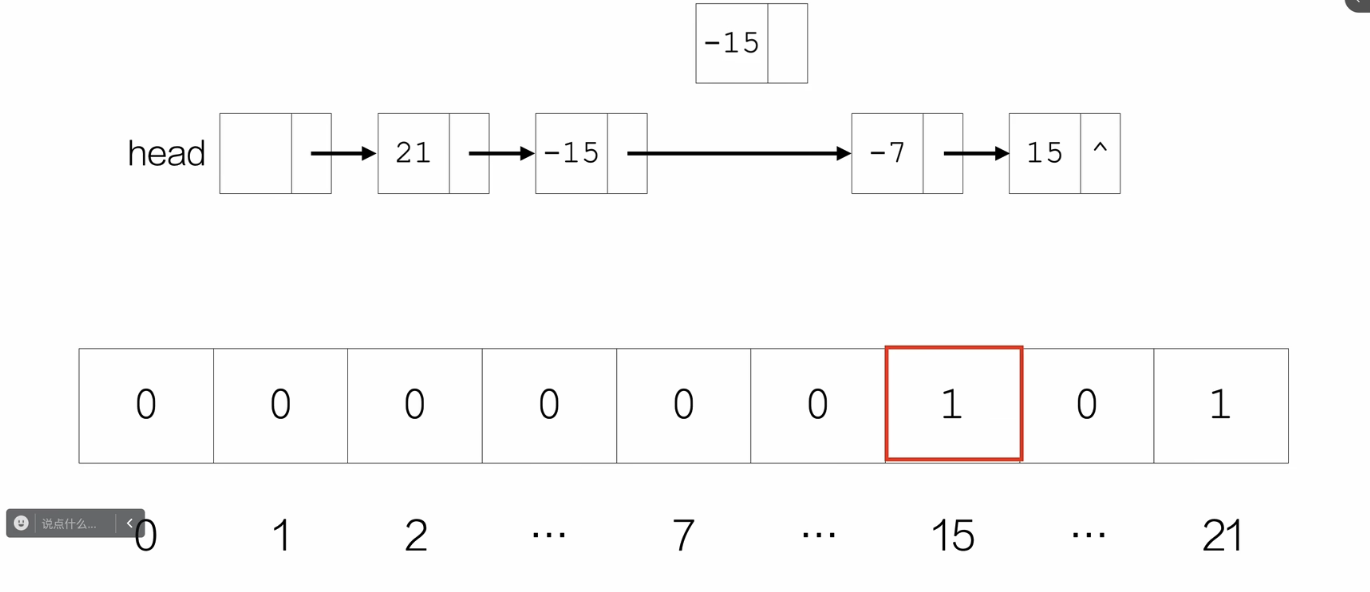
1742722361620

/*题3：删除绝对值相同的其余节点*/
//L: 链表头节点 n: |data|的最大值（和题目给的n没关系）
void removeNode_withAbsSame(Node* L,int n){
    Node *tmp = L;
    //数组下标
    int index;
    //数组
    int *arr = (int*)malloc(sizeof(int)*(n+1));
    //初始化全0数组
    for(int i = 0; i < n+1; i++){
        arr[i] = 0;
    }
    //遍历链表，和数组下标index比对
    //tmp是待比对节点的前驱节点
    //tmp->next是待比对节点
    while(tmp->next != NULL){
        index = abs(tmp->next->data);
        //待比对节点的data在数组下标中第一次出现为0
        if(arr[index] == 0){
            arr[index] = 1;
            tmp = tmp->next;
        } 
        //否则为1，已经出现过，就删除待比对节点
        else{
            Node *delNode = tmp->next;
            tmp->next = delNode->next;
            free(delNode);
        }
    }

}

int main(){
    Node *list = initList();
    Node *tail = getTail(list);
    tail = insertTail(tail,21);
    tail = insertTail(tail,-15);
    tail = insertTail(tail,-15);
    tail = insertTail(tail,7);
    tail = insertTail(tail,15);

    listNode(list);
    removeNode_withAbsSame(list,21);
    listNode(list);
  
    return 0;
}

1742721979318

反转链表

思路：三指针法

1742722551356

1742722560466

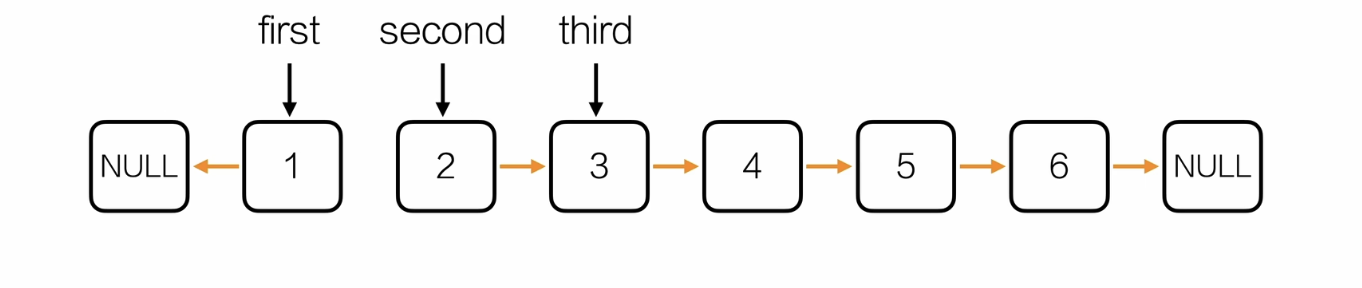
1742722574493

1742722586618

1742722689613

1742722765040

1742722698880

/*单链表应用——反转链表*/
Node* reverseList(Node *L){
    Node *first = NULL;
    Node *second = L->next;
    Node *third = NULL;

    //结束条件
    while(second != NULL){
        third = second->next;
        //改变箭头指向
        second->next = first;
        //从first开始向后挪
        first = second; 
        second = third;
    }
    //把原头节点与反转后的链表重新连接起来
    L->next = first;
    return L;
}

int main(){
    Node *list = initList();
    Node *tail = getTail(list);
    tail = insertTail(tail,1);
    tail = insertTail(tail,2);
    tail = insertTail(tail,3);
    tail = insertTail(tail,4);
    tail = insertTail(tail,5);
    tail = insertTail(tail,6);
    listNode(list);
    Node *reserveredList = reverseList(list);
    listNode(reserveredList);
}

删除单链表的中间节点

思路：

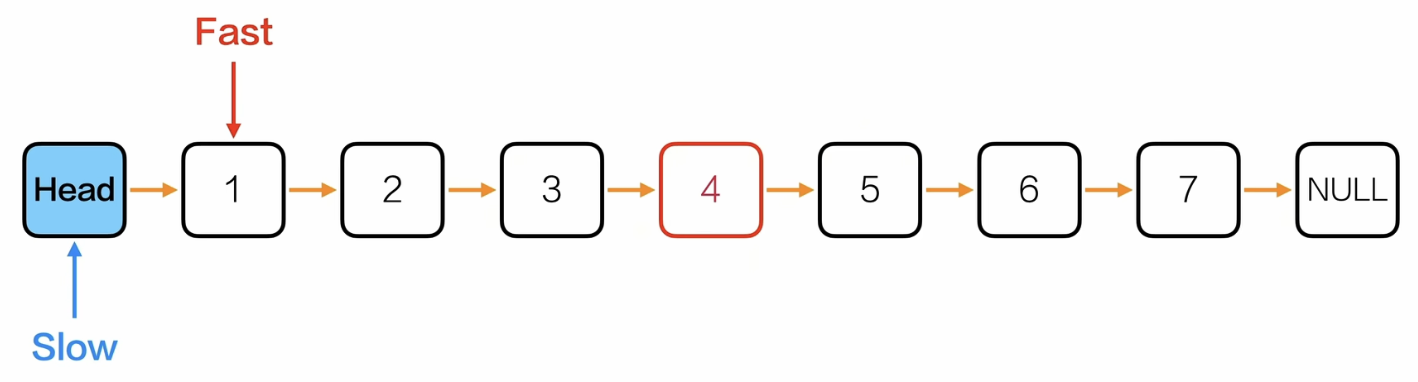
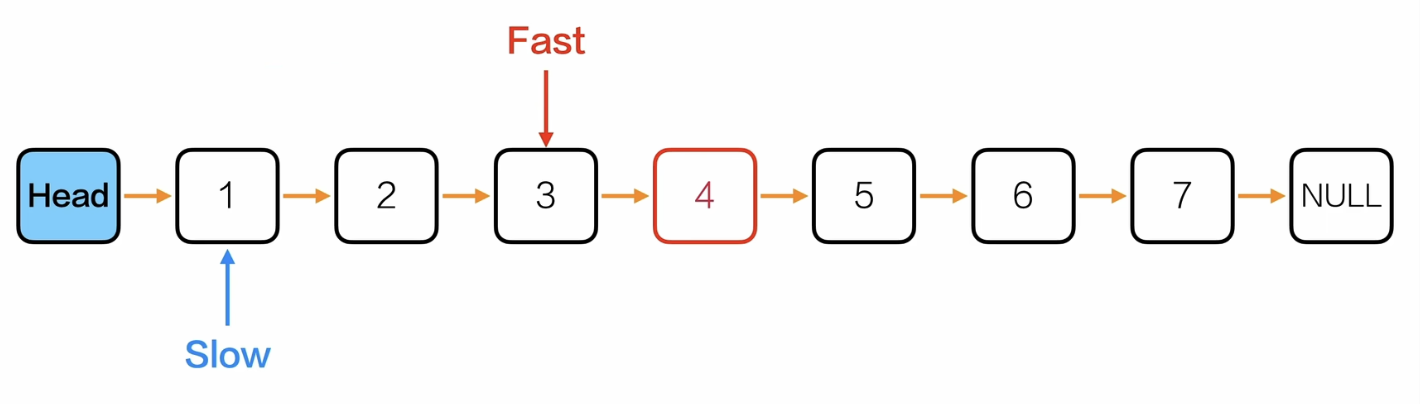
1743570114248 1743570137071

1743570151910

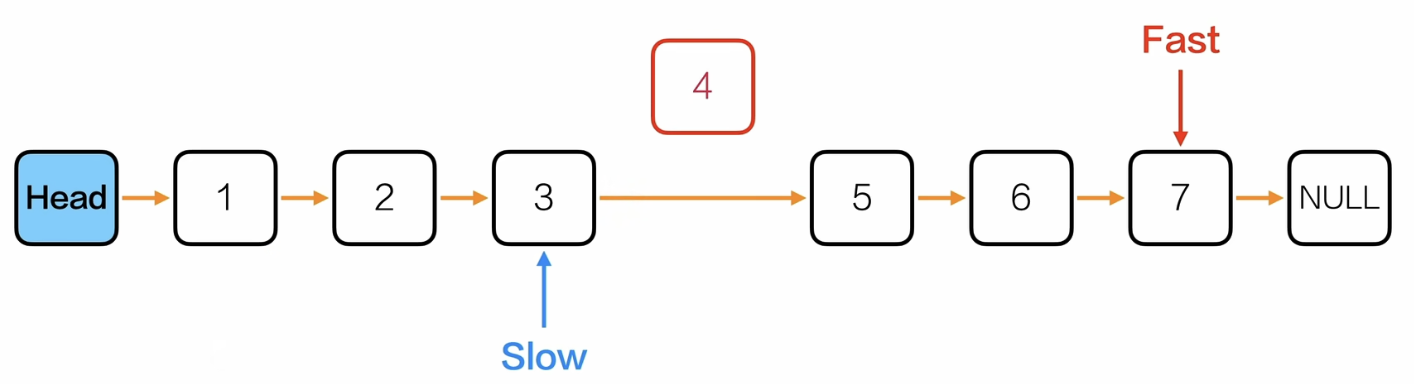
1743570166595

类比：同一个跑道，甲的速度是乙的两倍，那么甲到达终点的时候，乙就在中间。那么要删除这个中间节点的关键就是找到它的前驱节点。

上面的思路其实可以改成：

快慢指针都从头节点L开始，然后快指针每次走2，慢指针走1，结束条件是fast->next->next = NULL

/*单链表应用——删除中间节点*/
Node *deldMidNode(Node *L){
    Node *fast = L;
    Node *slow = L;

    //找到中间节点的前驱节点，也就是fast走到尾部的前一次时slow停留的位置
    while(fast->next->next!= NULL){
        fast = fast->next->next;
        slow = slow->next;
    }
    Node *delNode = slow->next;
    slow->next = delNode->next;
    free(delNode);
    return slow;
}

int main(){
    Node *list = initList();
    Node *tail = getTail(list);
    tail = insertTail(tail,1);
    tail = insertTail(tail,2);
    tail = insertTail(tail,3);
    tail = insertTail(tail,4);
    tail = insertTail(tail,5);
    tail = insertTail(tail,6);
    tail = insertTail(tail,7);

    listNode(list);
    printf("中间节点是：%d\n",deldMidNode(list)->data);
    listNode(list);
  
    return 0;
}

1743575400986

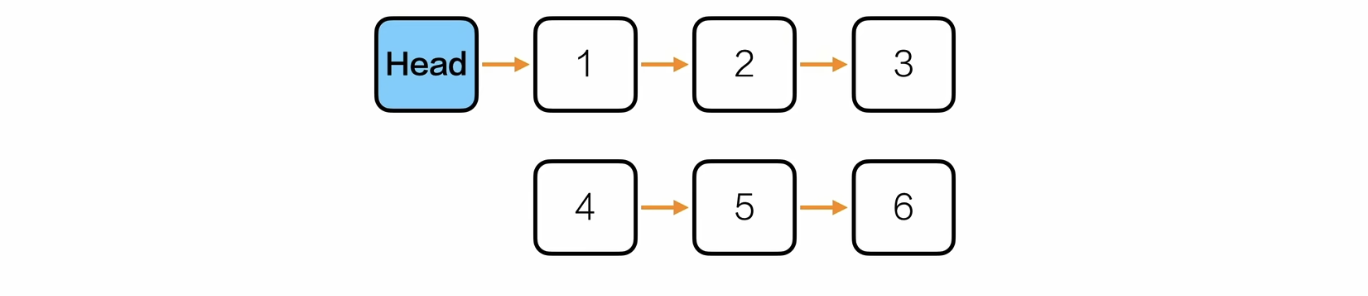
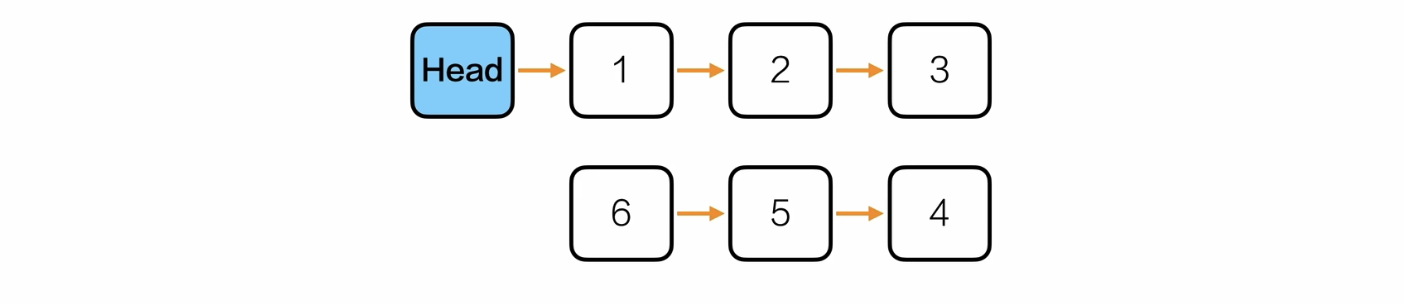
综合应用

结合 找出中间节点 和 反转链表 ，按一定规则重新排序

1743571471079

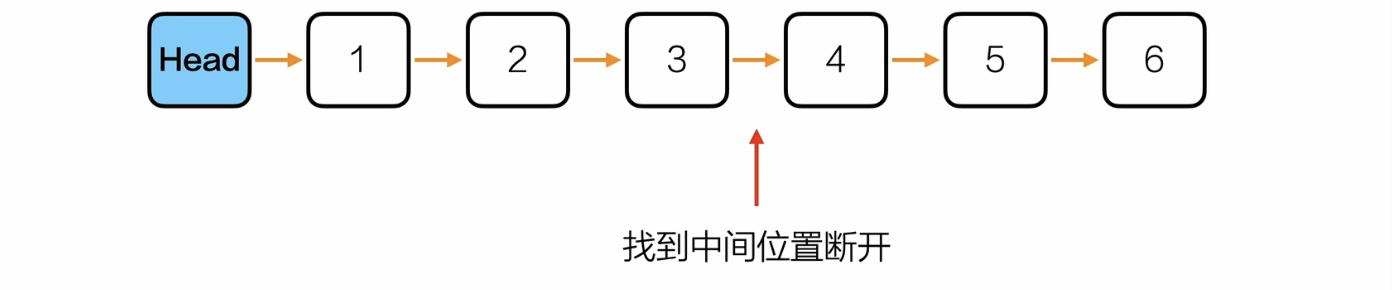
思路： 1743571924819

1743571932599

1743571942781

1743571973275

/*综合应用——重新排序*/
Node* reOrder(Node *L){
    Node *fast = L;
    Node *slow = L;
    while(fast!= NULL){  
        fast = fast->next->next;
        slow = slow->next;
    }
    //这时候slow就是中间节点

    //把链表分成两部分
    Node *L1 = L;
    Node *L2 = slow->next;
    slow->next = NULL;

    //反转L2
    //注意上面分好后，L2没有头节点，second = head->next = L2，所以second = L2
    Node *first = NULL;
    Node *second = L2;
    Node *third = NULL;

    while(second!= NULL){
        third = second->next;
        second->next = first;
        first = second;
        second = third;
    }
  
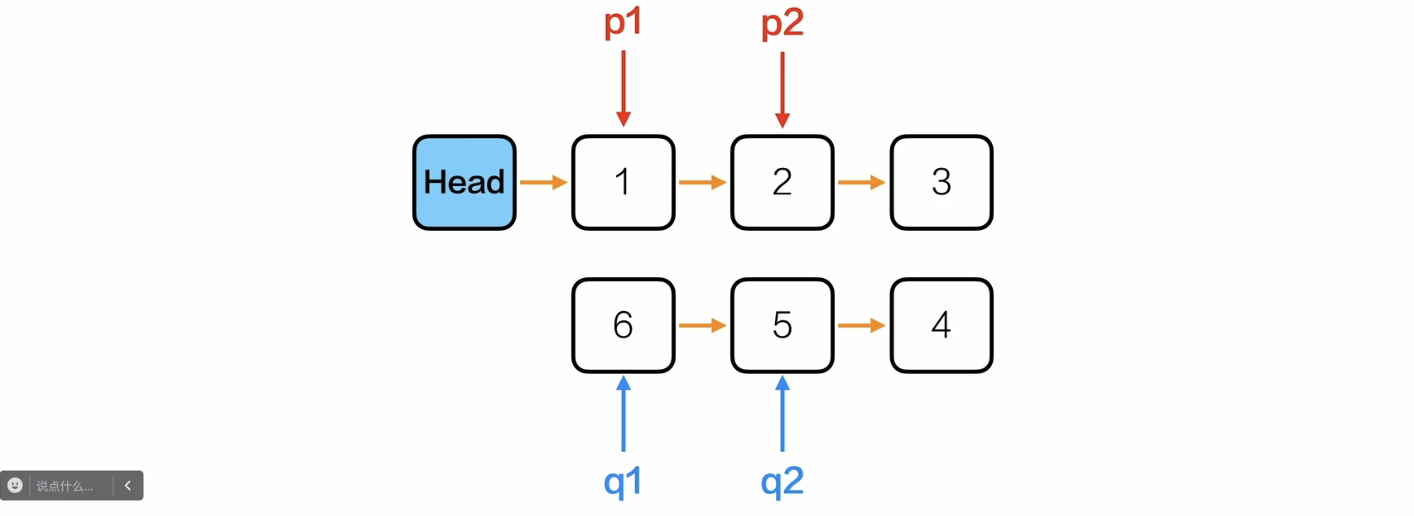
    //插入
    Node *p1 = L1->next;
    Node *q1 = first;
    Node *p2 = NULL;
    Node *q2 = NULL;
    while(p1!= NULL && q1!= NULL){
        p2 = p1->next;
        q2 = q1->next;
        //交替插入
        p1->next = q1;
        q1->next = p2;
        //向后更新指针
        p1 = p2;
        q1 = q2;
    }

    return L;
}

int main(){
    Node *list = initList();
    Node *tail = getTail(list);
    tail = insertTail(tail,1);
    tail = insertTail(tail,2);
    tail = insertTail(tail,3);
    tail = insertTail(tail,4);
    tail = insertTail(tail,5);
    tail = insertTail(tail,6);
    tail = insertTail(tail,7);

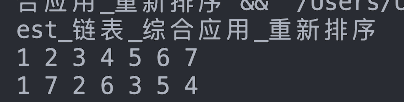
    listNode(list);
    Node *reOrderedList = reOrder(list);
    listNode(reOrderedList);
  
    return 0;

}

1743575305210

单向循环链表

和单链表的区别：遍历的终止条件不同

单链表	p != NULL 或者 p->next != NULL
单向循环链表	p != L 或者 p->next != L

判断链表是否有环

思路：快慢指针，二者相遇的时候就说明有环

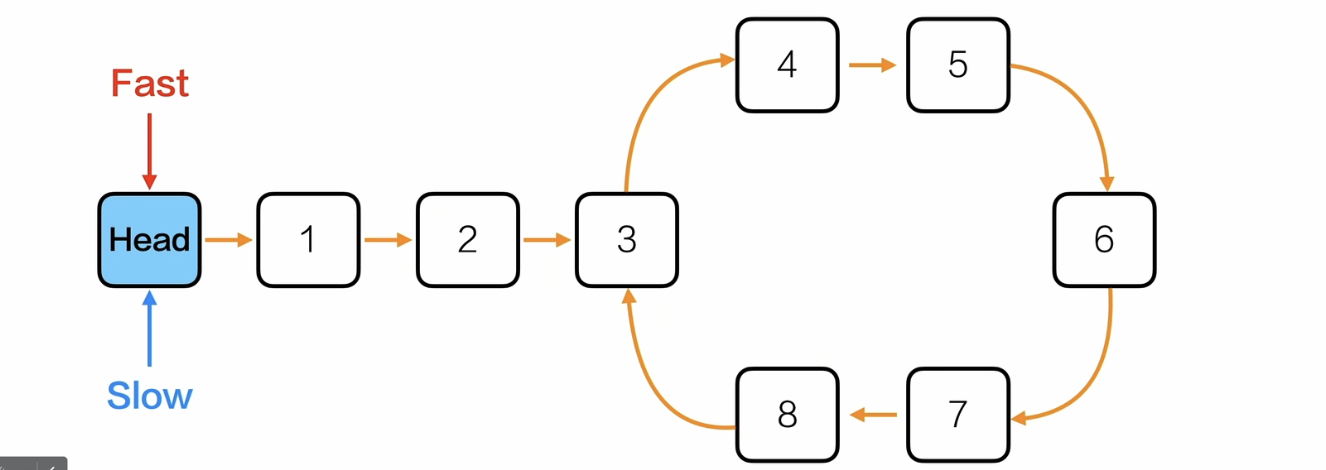
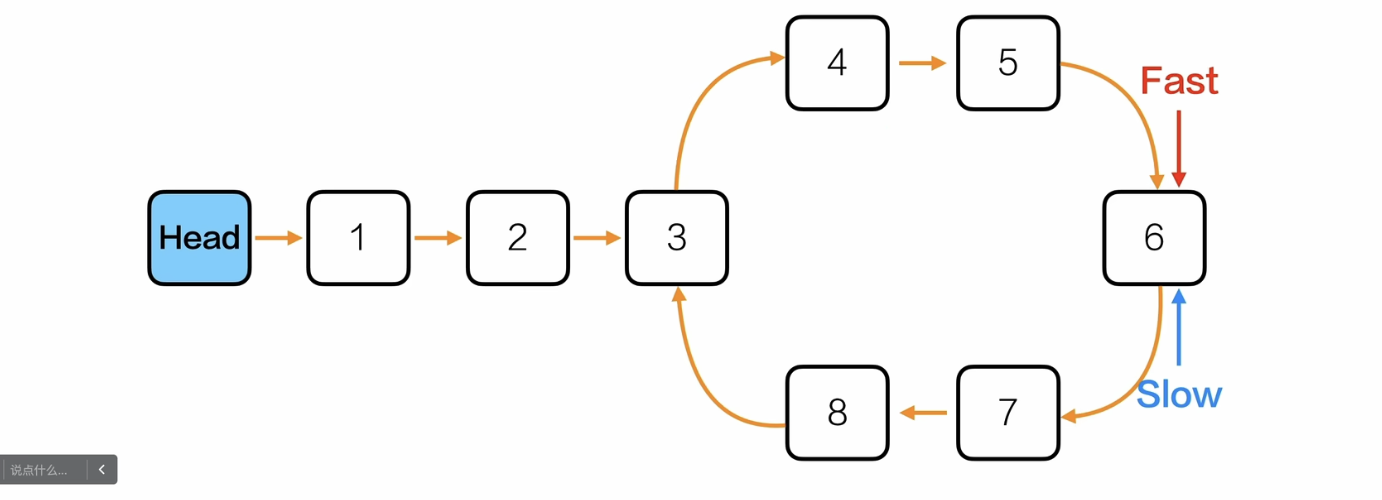
1743578456868 1743578467974

找到环的入口

方法一：

得到环的长度(其实在这一步快指针就已经比慢指针多走了一个环长了，所以有了下面更简便的方法二)
重置快慢指针到头节点，快指针先走一个环长，然后两个指针同步走，相遇的时候的节点是入口

/*找到环的入口*/
int findCircleEntry(Node *L){
    //先得到环的长度
    Node *slow = L;
    Node *fast = L;
    int circleStep = 0;
    while(fast != NULL && fast->next != NULL){
        fast = fast->next->next;
        slow = slow->next;
        circleStep++;
        if(fast == slow){
            break;
        }
    }
    printf("环的长度为：%d\n",circleStep);
  
    //初始化slow和fast指针为头节点
    slow = L;
    fast = L;
    for(int i = 0; i < circleStep; i++){
        fast = fast->next;
    }
    while(slow != NULL){
        fast = fast->next;
        slow = slow->next;
        if(fast == slow){
            return slow->data;
        }

    }
    return 0;
}

int main(){
    Node *list = initList();
    Node *tail = getTail(list);
    tail = insertTail(tail,1);
    tail = insertTail(tail,2);
    tail = insertTail(tail,3);
    Node *tmp = tail;
    tail = insertTail(tail,4);
    tail = insertTail(tail,5);
    tail = insertTail(tail,6);
    tail = insertTail(tail,7);
    tail = insertTail(tail,8);
    tail->next = tmp;
    if(isCircle(list)){
        printf("有环\n");
    }
    printf("环的入口为：%d\n",findCircleEntry(list));

    return 0;  
}

方法二：不用计算环长，在第一次相遇之后，只重置慢指针到头节点，然后两者同步走，第二次相遇就是入口。

法二的原理就是 快指针在第一次相遇的时候就已经比慢指针多走了6次了

/*找到环的入口*/
int findCircleEntry(Node *L){
    Node *slow = L;
    Node *fast = L;
    while(fast != NULL && fast->next != NULL){
        fast = fast->next->next;
        slow = slow->next;
        if(fast == slow){
            break;
        }
    }  
    //初始化slow和fast指针为头节点
    slow = L;
    while(slow != NULL){
        fast = fast->next;
        slow = slow->next;
        if(fast == slow){
            return slow->data;
        }

    }
    return 0;
}

int main(){
    Node *list = initList();
    Node *tail = getTail(list);
    tail = insertTail(tail,1);
    tail = insertTail(tail,2);
    tail = insertTail(tail,3);
    Node *tmp = tail;
    tail = insertTail(tail,4);
    tail = insertTail(tail,5);
    tail = insertTail(tail,6);
    tail = insertTail(tail,7);
    tail = insertTail(tail,8);
    tail->next = tmp;
    if(isCircle(list)){
        printf("有环\n");
    }
    printf("环的入口为：%d\n",findCircleEntry(list));

    return 0;  
}

1743581611291

双向链表

初始化、遍历、获取链表长度、释放内存和单链表一样

//初始化和单链表一样
/*单链表——初始化*/
Node* initList(){
    Node *head = (Node*)malloc(sizeof(Node));
    head->data = 0;
    head->next = NULL;
    return head;//返回头节点指针，头节点可以代表整个链表
}

//遍历和单链表一样
/*单链表——遍历*/
void listNode(Node *L){
    Node *tmp = L->next;
    while(tmp!= NULL){
        printf("%d ",tmp->data);
        //更新为下一个节点
        tmp = tmp->next;
    }
    printf("\n");
}

//获取链表长度和单链表一样
/*单链表——获取链表长度*/
int listLength(Node *L){
    Node *tmp = L;
    int len = 0;
    while(tmp != NULL){
        tmp = tmp->next;
        len++; 
    }
    return len;

}

//释放内存和单链表一样
/*单链表——释放内存*/
int listRealse(Node *L){
    Node *tmp = L->next;
    Node *q;

    if(tmp == NULL){
        printf("这个链表只有头节点，不用释放\n");
        return 0;
    }
    while(tmp != NULL){
        q = tmp->next;
        free(tmp);
        //向后更新tmp
        tmp = q;
    }
    L->next = NULL;
    return 0;
}

头插法

下图中的箭头是指针指向

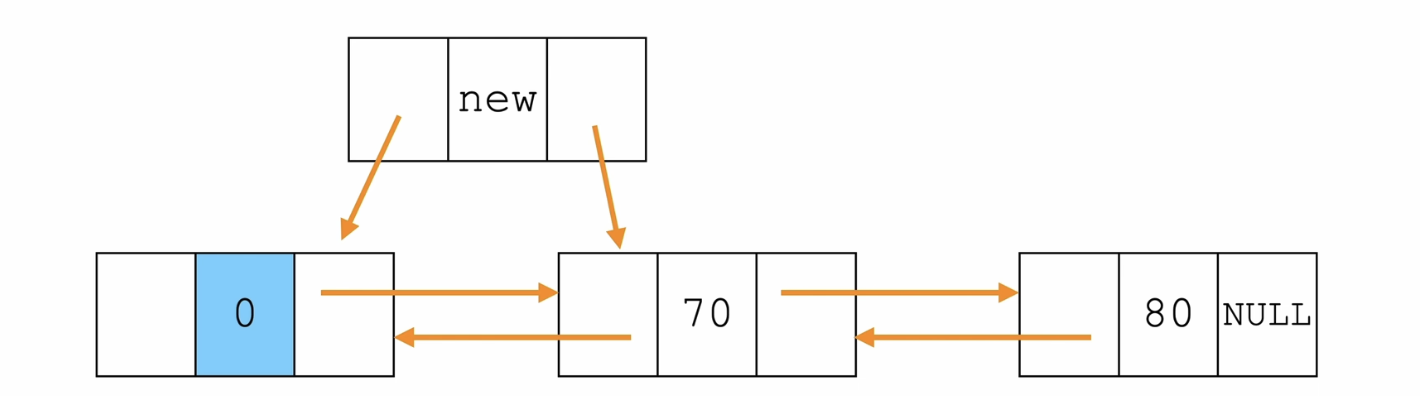
1743582208850

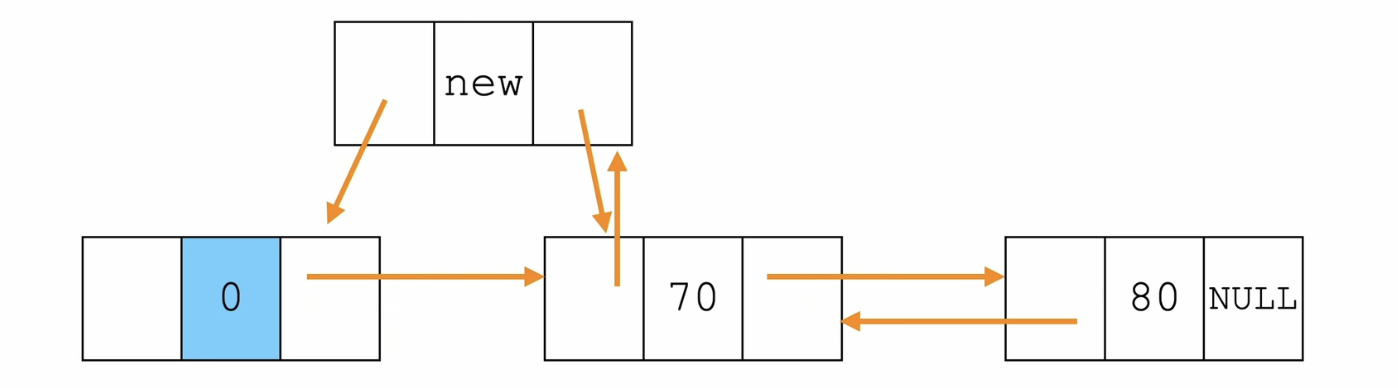
1743582219172

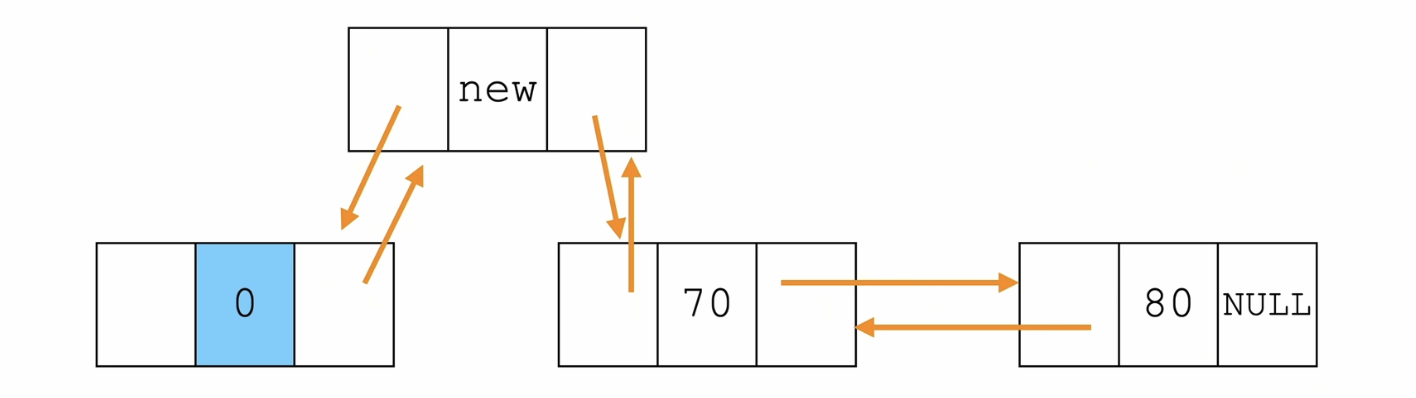
1743582233781

步骤：

新节点的前驱是头节点，后驱是头节点的next
头节点的next的前驱是新节点
头节点的后驱是新节点

/*双向链表——头插法*/
int insertHead(Node *L,ElemType elem){
    Node *p = (Node*)malloc(sizeof(Node));
    //新节点的前驱 是 头节点，后驱 是 头节点的后继节点
    p->data = elem;
    p->prev = L;
    p->next = L->next;
    //头节点的后继节点的前驱 是 新节点
    if(L->next!= NULL){
        L->next->prev = p;
    }
    //头节点的新后继节点 是 新节点
    L->next = p;
    return 1;
}

int main(){
    Node *list = initList();
    insertHead(list,1);
    insertHead(list,2);
    insertHead(list,3);
    insertHead(list,4);
    listNode(list);
    return 0;
}

1743584547167

尾插法

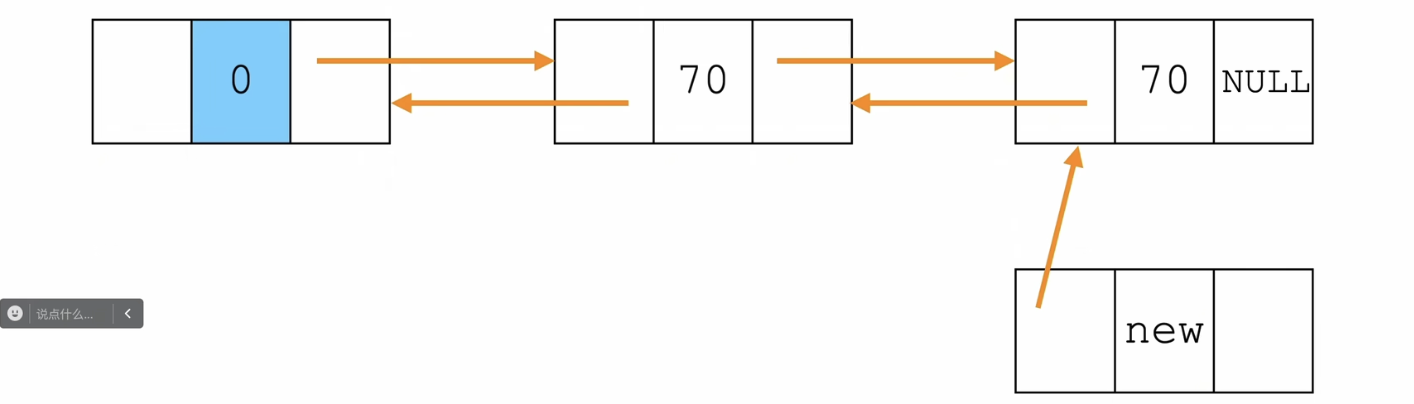
1743584703742

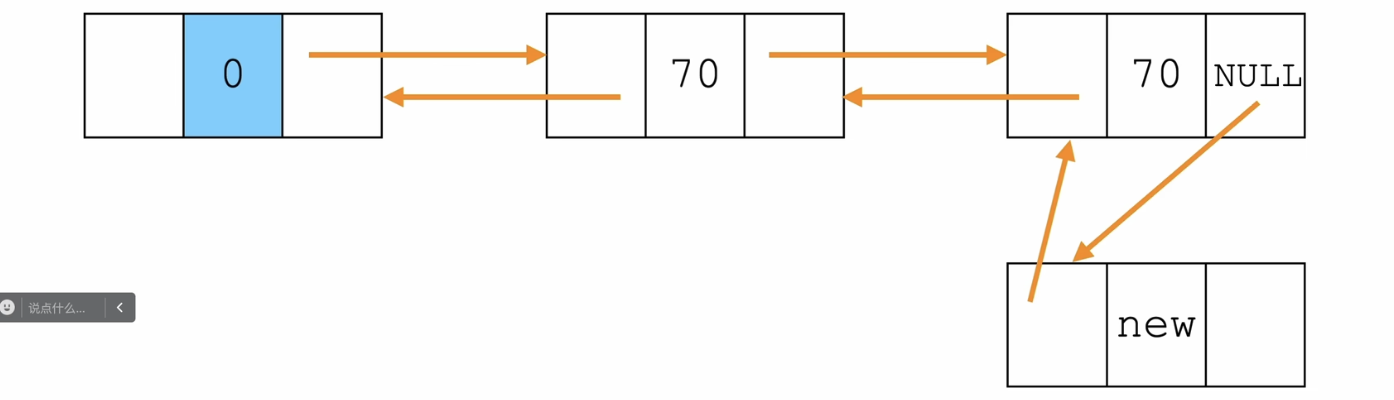
1743584717659

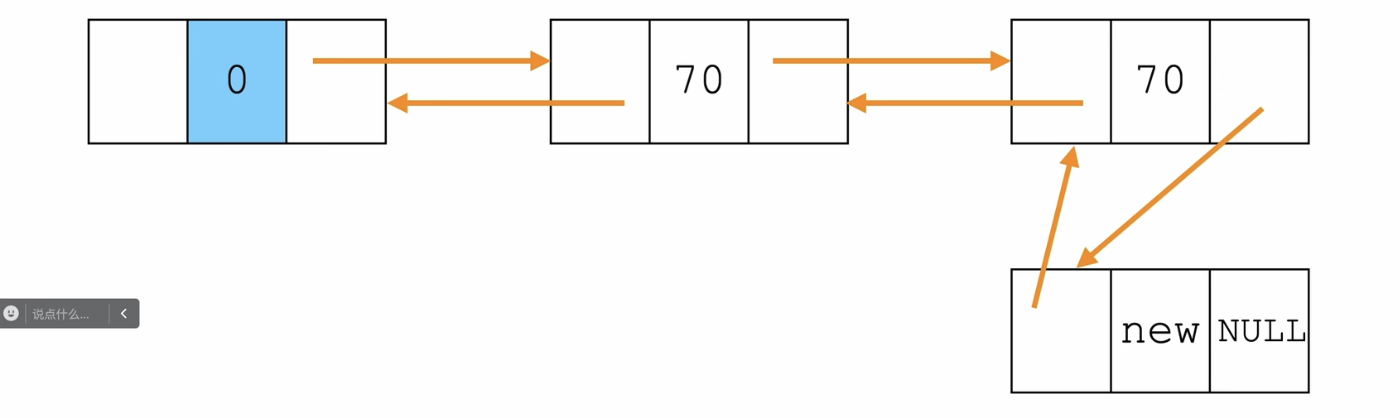
1743584851556

步骤：

新节点的前驱是尾节点
尾节点的后驱是新节点
给新节点的next赋值NULL，成为新的尾节点

/*双向链表——尾插法*/
//获取尾节点的方法和单链表一样
Node* getTail(Node *L){
    Node *tmp = L;
    while(tmp->next != NULL){
        tmp = tmp->next;
    }
    return tmp;
}
Node* insertTail(Node *tail,ElemType elem){
    Node* tmp = (Node*)malloc(sizeof(Node));
    tmp->data = elem;
    tmp->prev = tail;
    tail->next = tmp;
    //更新尾节点指针
    tmp->next = NULL;
    return tmp;
}

int main(){
    Node *list = initList();
    Node *tail = getTail(list);
    tail = insertTail(tail,1);
    tail = insertTail(tail,2);
    tail = insertTail(tail,3);
    listNode(list);
    return 0;
}

1743584609124

在指定位置插入数据

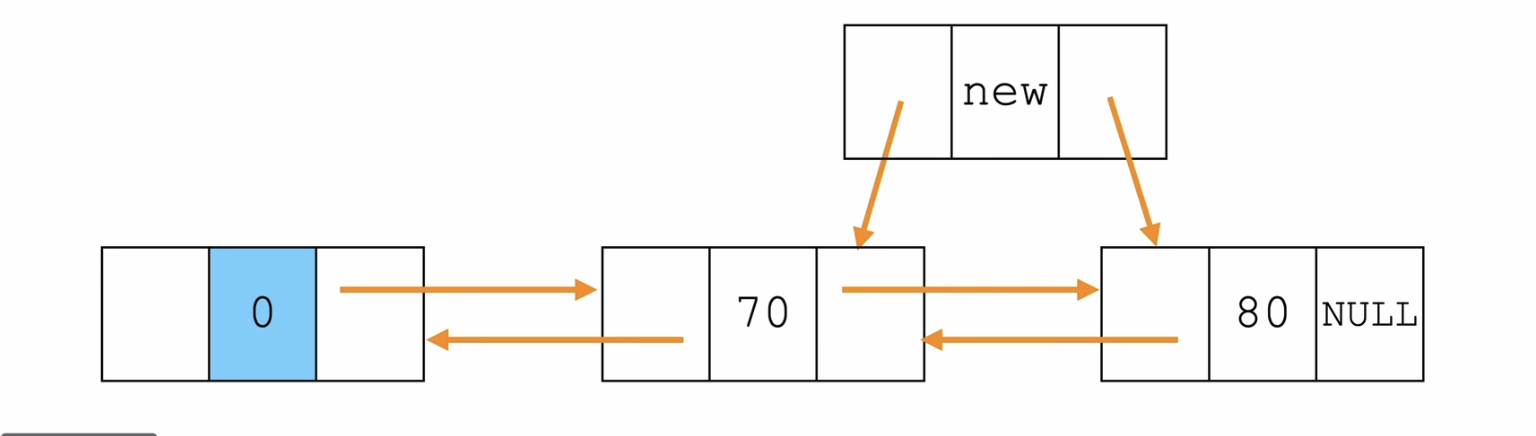
1743585257682

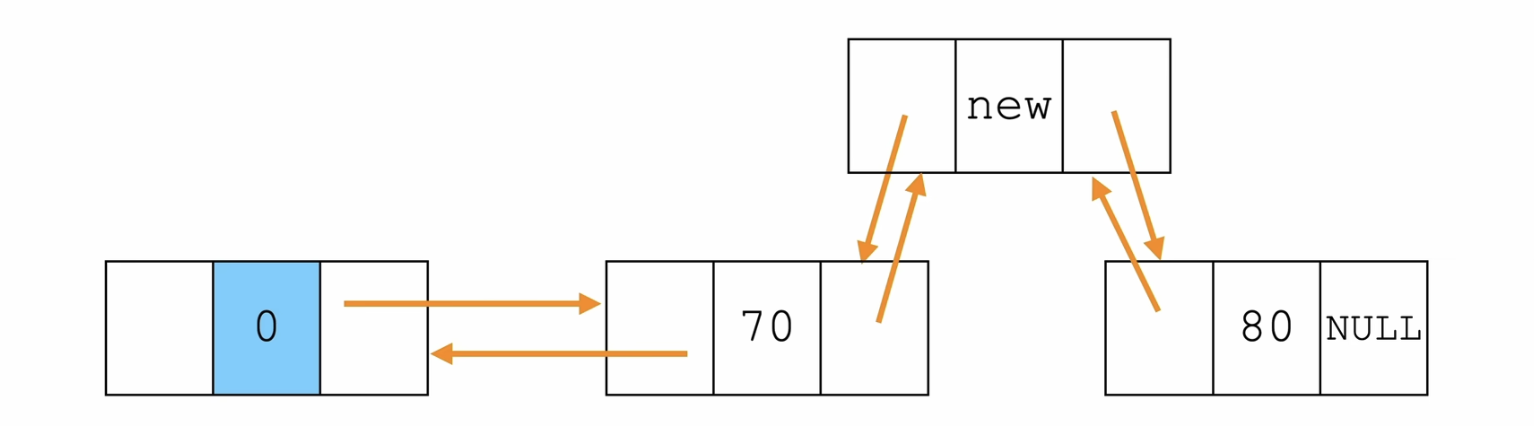
1743585268090

步骤：

新节点的前驱和后驱分别是指定节点和指定节点的next
指定节点的next的前驱是新节点，指定节点的后驱是新节点

/*双向链表——指定位置插入节点*/
int insertPos(Node *L,int targetIndex,ElemType elem){
    //获取目标位置的前驱节点
    Node *p = L;
    //如果定义的是L->next，下面获取的就是指定位置的后驱节点
    for(int i = 0;i < targetIndex;i++){
        p = p->next;
    }
    Node *tmp = (Node*)malloc(sizeof(Node));
    tmp->data = elem;
    tmp->prev = p;
    tmp->next = p->next;
  
    p->next->prev = tmp;
    p->next = tmp;
    return 1;
}

int main(){
    Node *list = initList();
    Node *tail = getTail(list);
    tail = insertTail(tail,1);
    tail = insertTail(tail,2);
    tail = insertTail(tail,3);
    listNode(list);
    insertPos(list,1,99);
    listNode(list);
    return 0;
}

1743586351903

删除节点

1743586512807

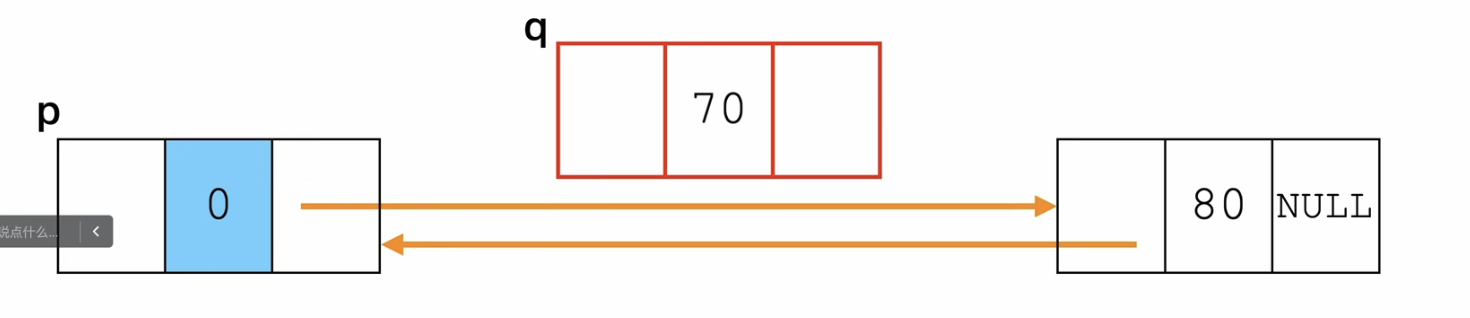
1743586518828

步骤：

遍历找到del节点的前驱节点
记录del节点
前驱节点的后驱是 del节点的next
del节点的next的前驱是前驱节点

/*双向链表——删除指定位置的节点*/
Node* delNode(Node *L,int targetIndex){
    //获取前驱节点
    Node *p = L;
    for(int i = 0;i < targetIndex;i++){
        p = p->next;
        if(p == NULL){
            return 0;
        }
    }
    //记录要删除的节点
    Node *del = p->next;
    //如果要删除的节点不存在
    if(del == NULL){
        printf("要删除的节点不存在\n");
        return 0;
    }
    //如果要删除的是尾节点，则直接更新尾节点指针为前驱节点
    else if(del->next == NULL) {
        p->next = NULL; 
        return L;
    } 

    p->next = del->next;
    del->next->prev = p;
    free(del);
    return L;
}

int main(){
    Node *list = initList();
    Node *tail = getTail(list);
    tail = insertTail(tail,1);
    tail = insertTail(tail,2);
    tail = insertTail(tail,3);
    listNode(list);
    insertPos(list,1,99);
    listNode(list);
    delNode(list,1);
    listNode(list);
    return 0;
}

1743588005129

总结：顺序表vs链表

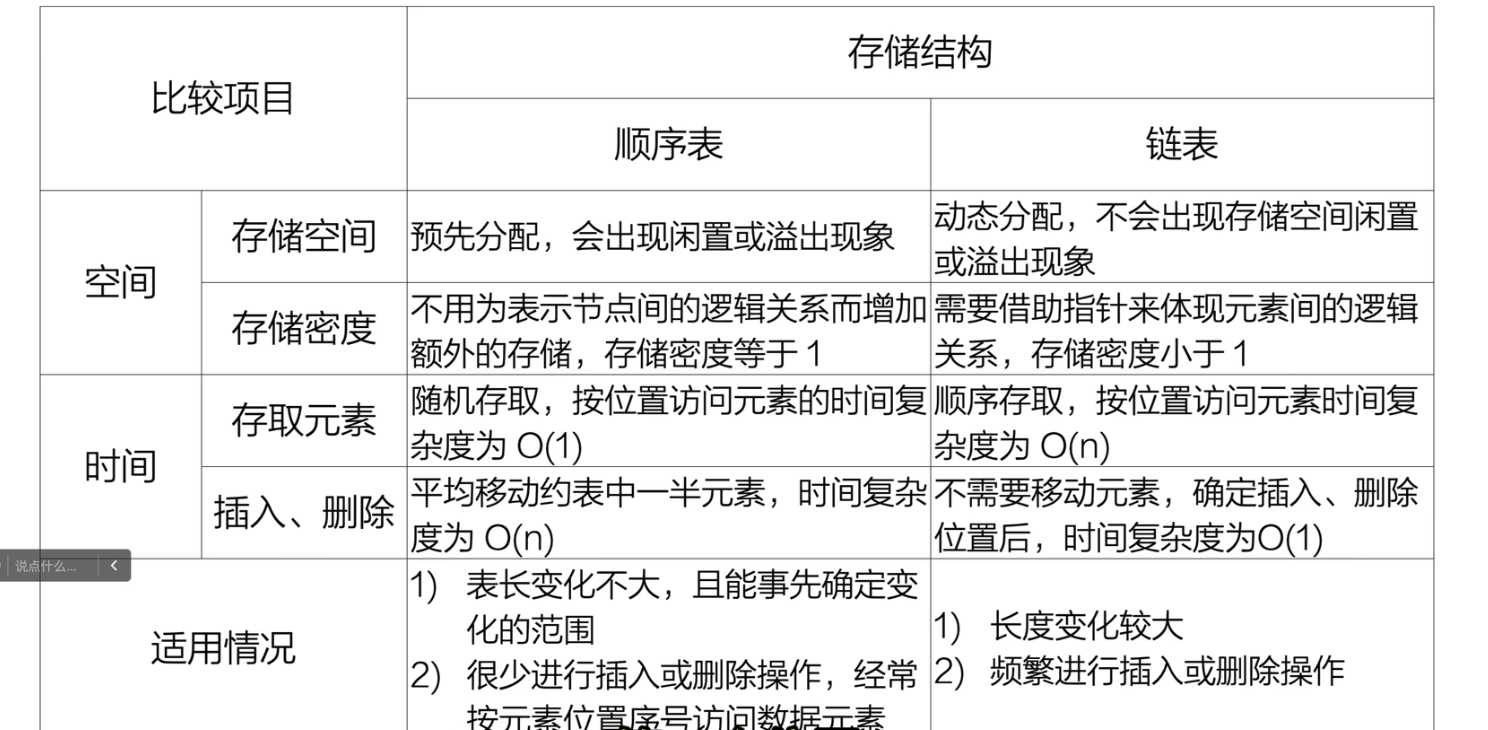
1743588154833

综合习题：

题一

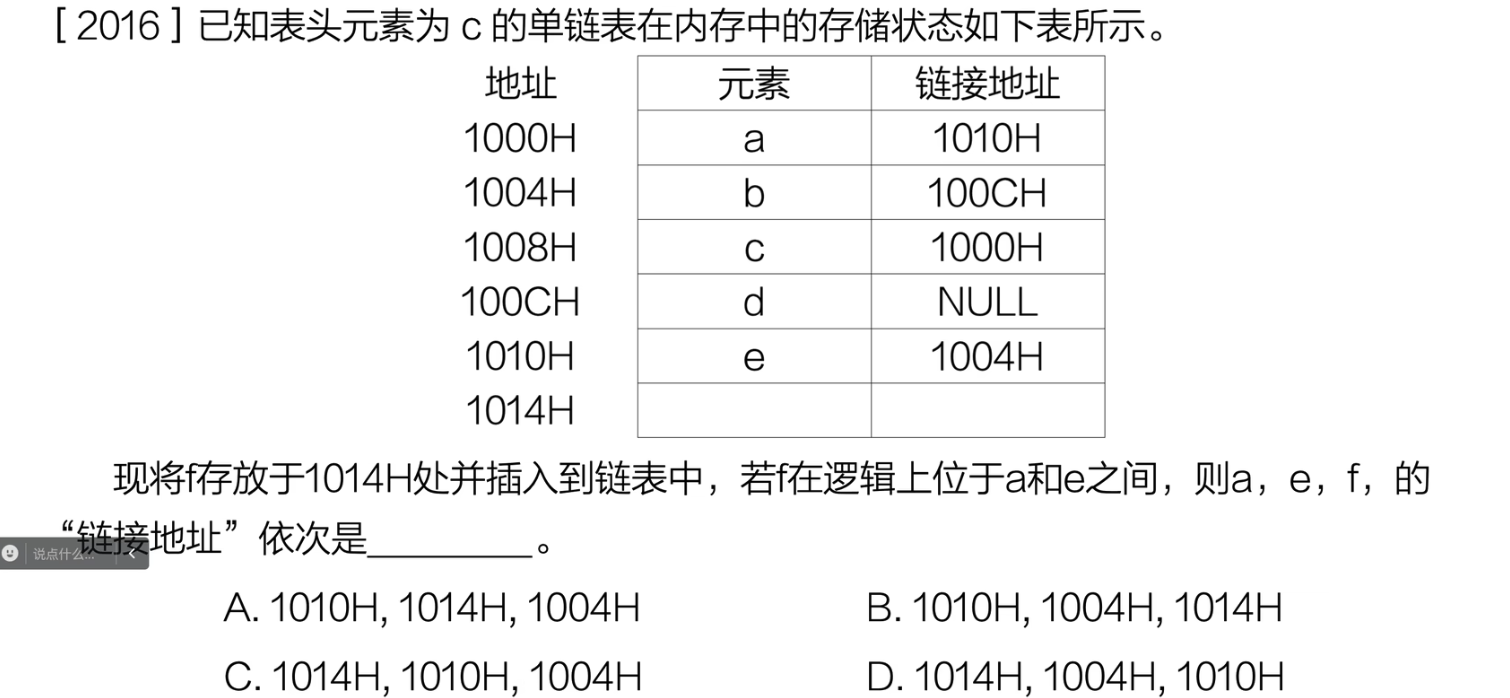
1743609025948

分析：

	c	a	e	b	d
地址	1008H	1000H	1010H	1004H	100CH	NULL

插入后，

	c	a	f	e	b	d
地址	1008H	1000H	1014H	1010H	1004H	100CH	NULL

所以a，f，e的链接地址(链表中的next)是：1014H，1010H，1004H

a，e，f就是：1014H，1004H，1010H

选D

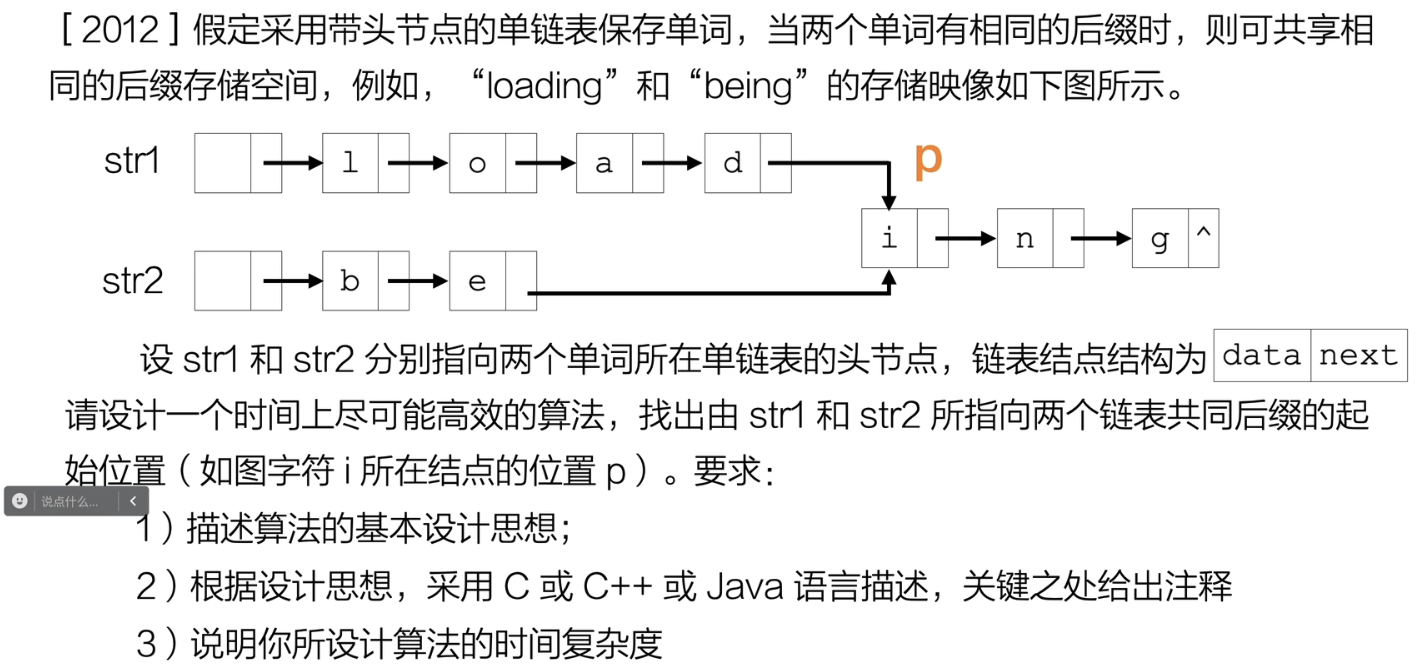
题二

1743670778123

p->next->prev = p->prev;

p->prev->next = p->next;

free(p);

选D

posted @ 2025-04-24 21:40 EanoJiang 阅读(53) 评论(0) 收藏举报

刷新页面返回顶部

eanojiang

线性表

线性表

顺序表(数组)

初始化

在尾部添加元素

遍历顺序表

插入元素

删除元素

查找

动态分配内存地址

链表

初始化

遍历

尾插法

在指定位置插入数据

删除节点

获取链表的长度

释放链表

单链表应用

双指针法

标志位法

反转链表

删除单链表的中间节点

综合应用

单向循环链表

判断链表是否有环

找到环的入口

双向链表

初始化、遍历、获取链表长度、释放内存和单链表一样

头插法

尾插法

在指定位置插入数据

删除节点

总结：顺序表vs链表

综合习题：

题一

题二

公告