Hello算法——数组与链表
4.1 数组(array)
4.1.1 数组基操
- 初始化数组
int arr[5] = { 0 };
int nums[5] = [1,5,6,21,4]
- 访问元素
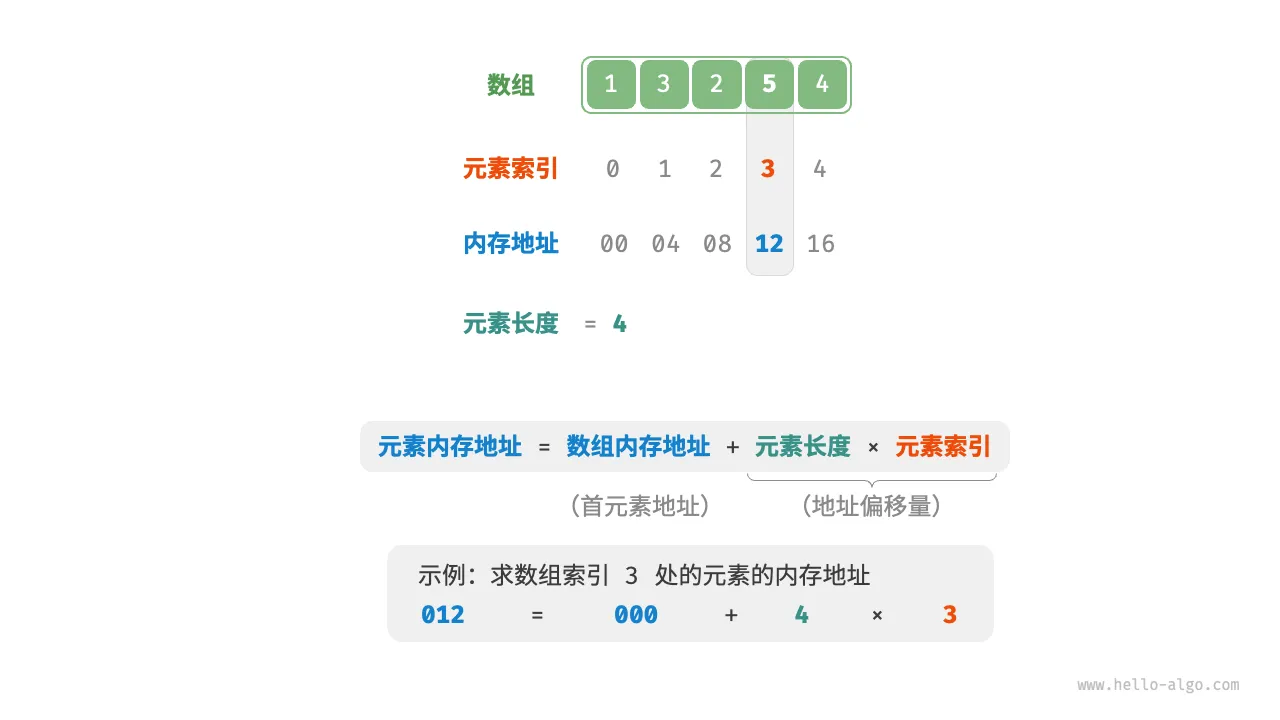
//访问元素
// 随机访问
int randomAccess(int *nums, int size){
int randomIndex = rand() % size;
// size = sizeof(nums) / sizeof(nums[0]);
int randomNumd = nums[randomIndex];
return randomNumd;
}
- 插入元素
如果想在数组中间插入一个元素,则需要将该元素之后的所有元素都向后移动一位,之后再把元素赋值给该索引。
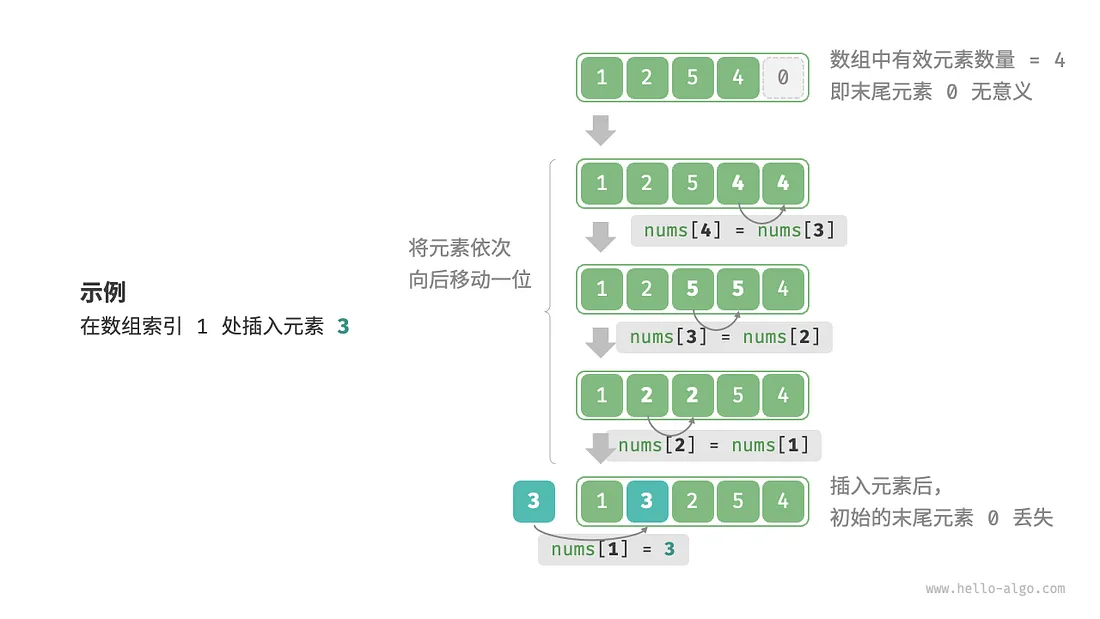
// 插入元素(在index位置插入num)
void insert(int *nums, int size, int num, int index){
for(int i = size - 1; i > index; i--){
nums[i] = nums[i - 1];
}
nums[index] = num;
}
- 删除元素
删除索引 i 处的元素,则需要把索引 i 之后的元素都向前移动一位。
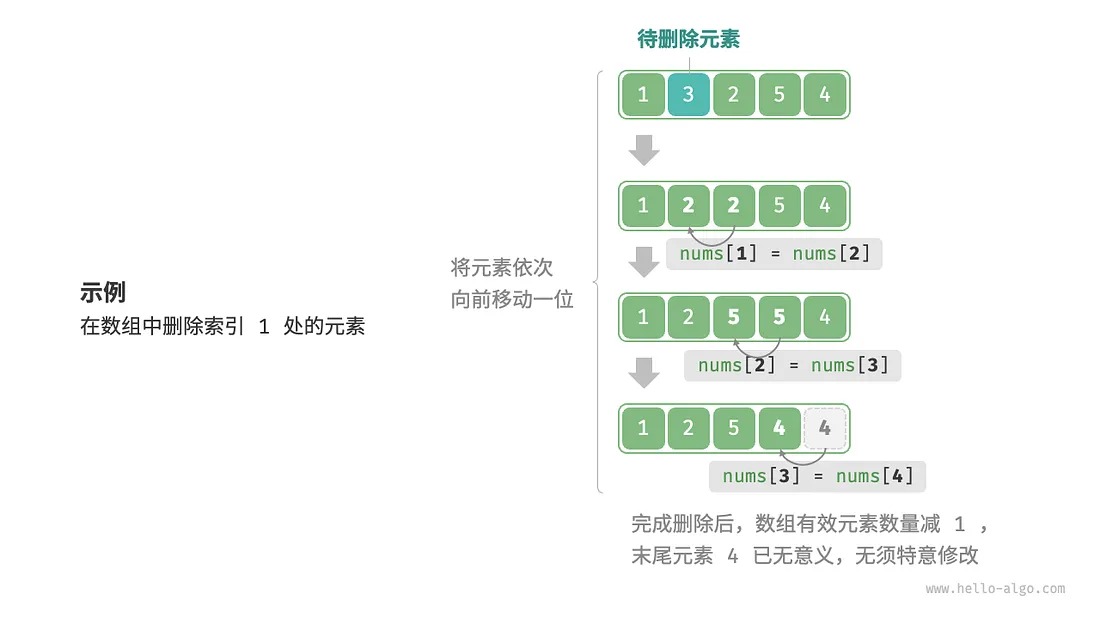
// 删除元素(删除index位置的元素)
// 注意:stdio.h 占用了 remove 关键词
void removeItem(int *nums, int size, int index){
for(int i = size - 1; i < index; i++){
nums[i] = nums[i + 1];
}
}
数组的插入与删除操作的缺点:
- 时间复杂度均为O(n)。
- 超出数组长度范围的元素会丢失。
- 内存浪费:初始化的时候通常会给出余量,这样在插入元素的时候丢失的末尾元素都无意义。
- 遍历数组
通过索引遍历数组
// 遍历数组
void traverse(int *nums, int size){
int temp = 0;
for (int i = 0; i < size; i++){
temp = nums[i];
printf("num = %d\n", temp);
}
}
- 查找元素(也称为线性查找)
遍历数组,每轮判断元素值是否匹配,若匹配则输出对应索引。
// 查找元素
int search(int *nums, int size, int target){
for (int i = 0; i < size; i++){
if (nums[i] == target){
return i;
}
}
return -1; // 未找到元素,返回一个不可能出现的索引值
}
- 扩容数组
遍历数组,每轮判断元素值是否匹配,若匹配则输出对应索引。
时间复杂度是O(n)
// 扩展数组
int *extendArray(int *nums, int size, int newSize){
// 新数组的动态内存分配
int *newNums = (int *)malloc(newSize * sizeof(int));
// 把原数组的元素依次添加到新数组中
for (int i = 0; i< size; i++){
newNums[i] = nums[i];
}
// 初始化新数组中剩余的元素
for (int i = size; i < newSize; i++){
newNums[i] = 0;
}
return newNums;
}
4.1.2 数组的优点与局限性
数组存储在连续的内存空间内,且元素类型相同。
- 空间效率高:数组为数据分配了连续的内存块,无须额外的结构开销。
- 支持随机访问:数组允许在 O(1) 时间内访问任何元素。
- 缓存局部性:当访问数组元素时,计算机不仅会加载它,还会缓存其周围的其他数据,从而借助高速缓存来提升后续操作的执行速度。
局限性:
- 插入与删除效率低:当数组中元素较多时,插入与删除操作需要移动大量的元素。
- 长度不可变:数组在初始化后长度就固定了,扩容数组需要将所有数据复制到新数组,开销很大。
- 空间浪费:如果数组分配的大小超过实际所需,那么多余的空间就被浪费了。
4.1.3 应用
- 随机访问
- 排序、搜索算法
- 查找表
- 机器学习
- 实现栈、队列、哈希表、堆、图等数据结构
4.2 链表(linked list)
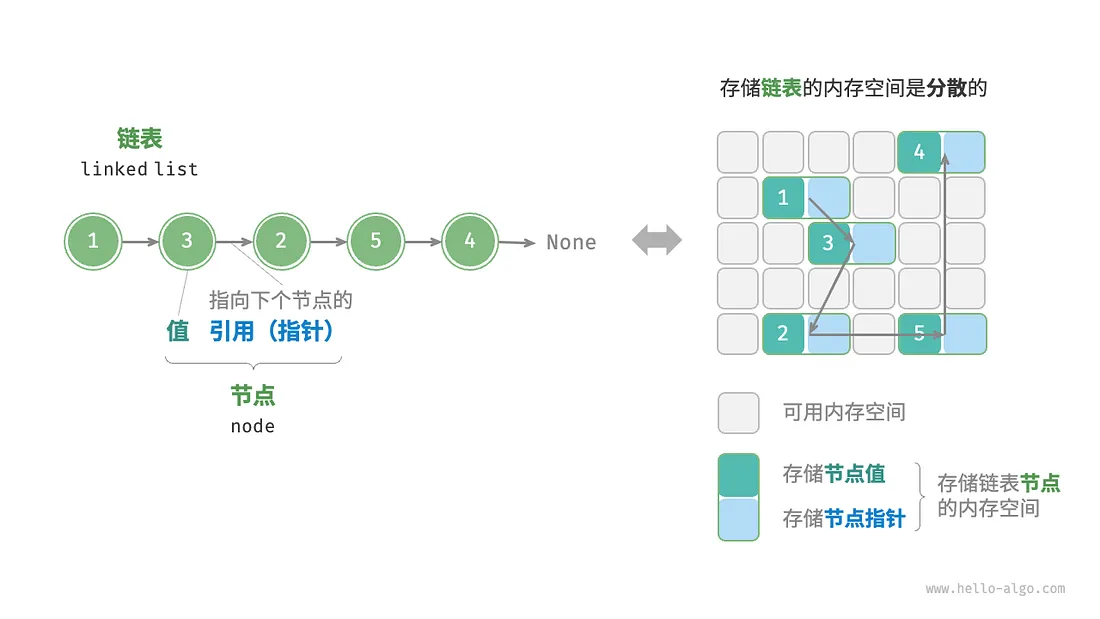
- 链表的组成单位是节点(node)
- 每个节点含 值、引用(指向下一节点的指针)。
- 尾节点指向“空”(C:nullptr)
- 链表比数组占用更多的内存空间(多出来的部分:引用(指针))
#include <stdio.h>
#include <stdlib.h>
typedef struct ListNode{
int val;
struct ListNode *next;
}ListNode;
ListNode *newListNode(int val){
ListNode *node;
node = (ListNode *)malloc(sizeof(ListNode));
node -> val = val;
node -> next = NULL;
return node;
}
4.2.1 链表基操
- 初始化链表
- 初始化各节点
- 建立节点间的引用关系
通常用头节点代指链表,比如下面的链表可以叫作n0
//初始化链表
int main(){
ListNode* n0 = newListNode(3);
ListNode* n1 = newListNode(9);
ListNode* n2 = newListNode(7);
ListNode* n3 = newListNode(2);
n0 -> next = n1;
n1 -> next = n2;
n2 -> next = n3;
n3 -> next = NULL;
}
遍历链表:
//遍历链表
void traverse(ListNode* head){
for (ListNode* i = head; i != NULL; i = i -> next){
printf("%d", i -> val); //打印节点的值 node->val
if(i -> next!= NULL)
printf(" -> ");
}
}
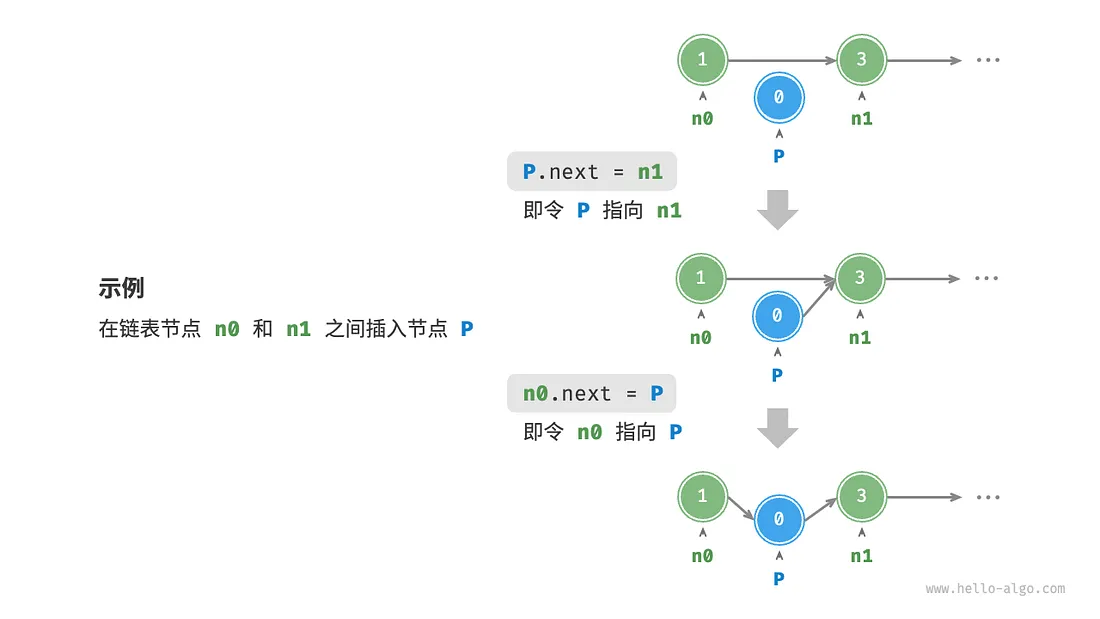
- 插入节点
在相邻节点间插入新节点p,只需要改变两个节点的引用(指针)即可。
链表插入节点的时间复杂度为O(1)
对比:数组插入元素的时间复杂度是O(n)
//插入节点
void insert(ListNode* node1, ListNode* node2, ListNode* p){
node1 -> next = p;
p -> next = node2;
}
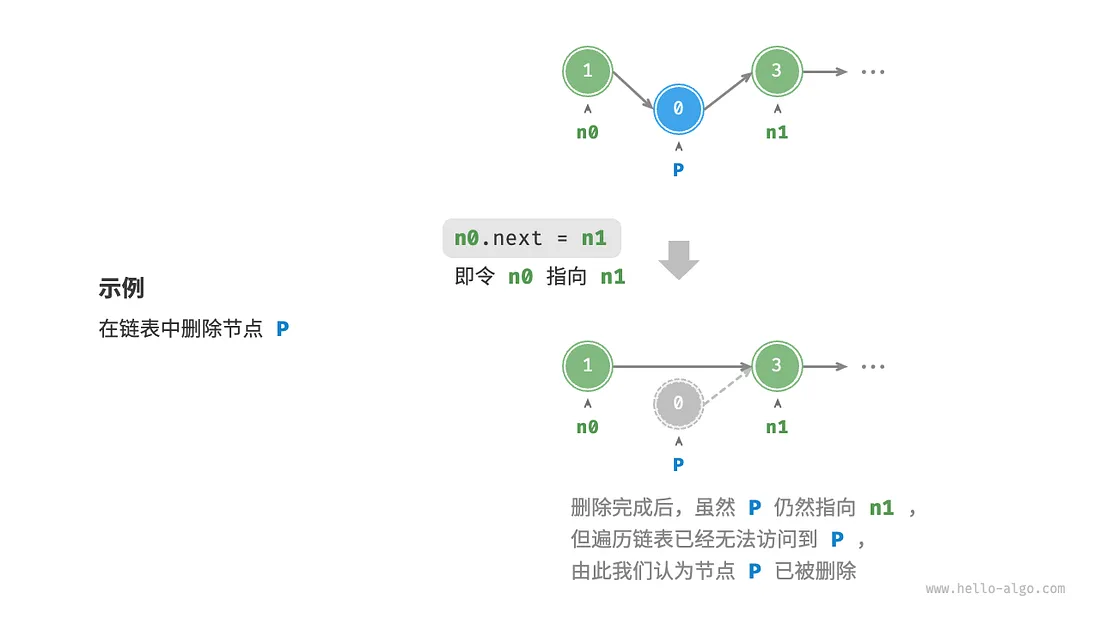
- 删除节点
也是只需要改变一个节点的引用(指针)即可。
//删除节点
// 删除node1 后的 第一个节点
void removeNode(ListNode* node1){
if(! node1 -> next){
return;
}
//node1 -> p -> node2
ListNode* p = node1 -> next; //把node1 后的第一个节点记作p
ListNode* node2 = p -> next; //把p 后的第一个节点记作node2
//node1 -> node2
node1 -> next = node2;
free(p);
}
- 访问节点
- 链表访问节点效率很低,需要从头节点开始遍历,直到找到目标节点再访问。
- 假如要访问第i个节点,则需要循环i-1次(第一个节点遍历到第i个节点)
- 时间复杂度O(n)
对比:数组的访问元素可以在O(1)的时间复杂度下访问任一元素。
//访问节点
ListNode* searchNode(ListNode* head,int index){
for(int i = 0;i < index; i++){
if(head == NULL)
return NULL;
head = head -> next; //更新head为下一个节点
}
return head;
}
- 查找节点
- 和访问节点一样,需要遍历链表到target节点,然后返回这个节点的索引。
- 属于线性查找。
//查找节点(的索引)
int search(ListNode* head,int target){
for(int index = 0; head != NULL; index++){
if(head ->val == target){
return index;
}
head = head -> next; //更新head为下一个节点
}
return -1; //未找到,返回一个不可能存在的索引
}
4.2.2 数组 vs. 链表
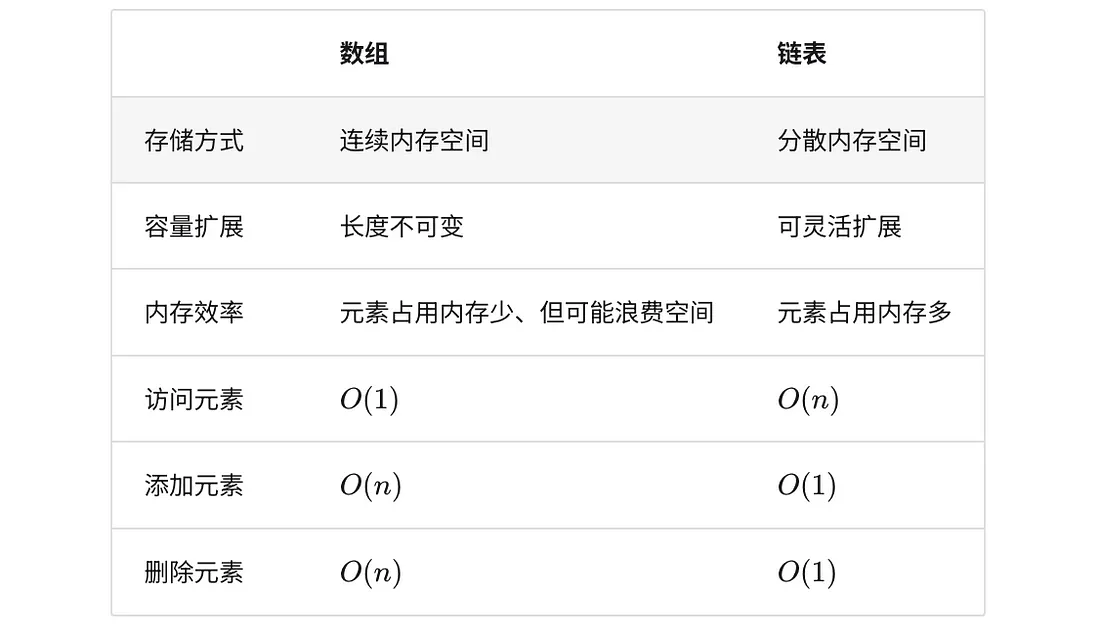
4.2.3 常见链表类型
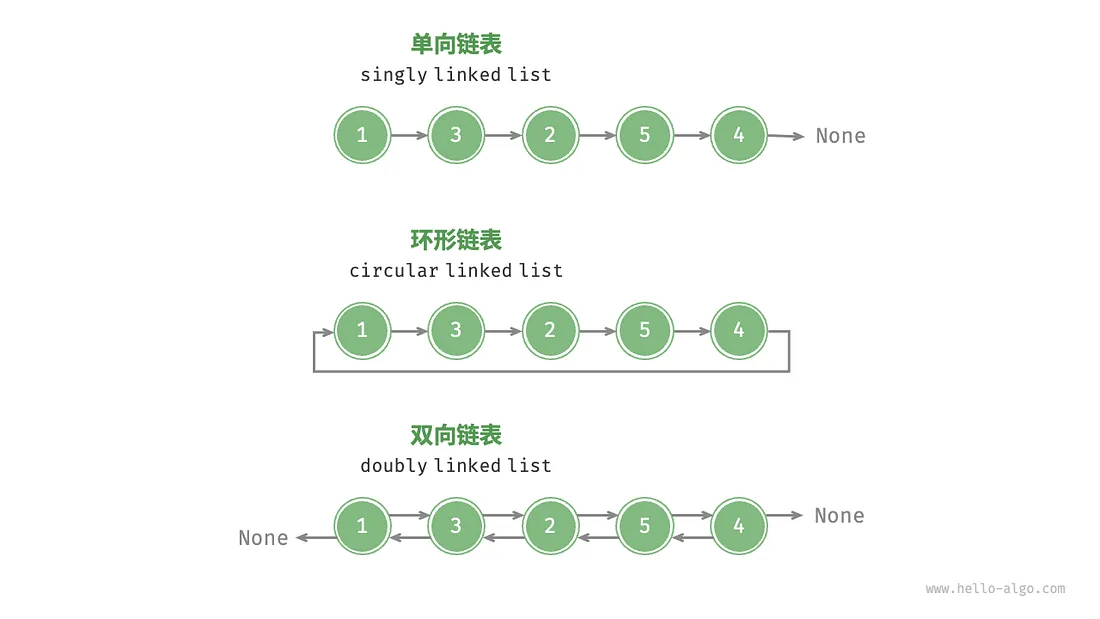
- 单向链表(也就是前面举例的普通链表)
- 环形链表:尾节点 -> 头节点(首尾相接),环形链表中的任一节点都可以是头节点。
- 双向链表:每个节点包含节点值、两个引用(前驱节点和后继节点的指针)
#include <stdio.h>
//双向链表的结构体
typedef struct DoubleLinkedList{
int val; //节点值
struct DoubleLinkedList* prev;
struct DoubleLinkedList* next;
}DoubleLinkedList;
//节点创建函数
DoubleLinkedList* newDoubleLinkedList(int val){
DoubleLinkedList* node = (DoubleLinkedList*)malloc(sizeof(DoubleLinkedList));
node -> val = val;
node -> prev = NULL;
node -> next = NULL;
return node;
}
4.2.4 链表的应用
单向链表通常用于实现栈、队列、哈希表和图等数据结构。
- 栈与队列:当插入和删除操作都在链表的一端进行时,它表现的特性为先进后出,对应栈;当插入操作在链表的一端进行,删除操作在链表的另一端进行,它表现的特性为先进先出,对应队列。
- 哈希表:链式地址是解决哈希冲突的主流方案之一,在该方案中,所有冲突的元素都会被放到一个链表中。
- 图:邻接表是表示图的一种常用方式,其中图的每个顶点都与一个链表相关联,链表中的每个元素都代表与该顶点相连的其他顶点。
双向链表常用于需要快速查找前一个和后一个元素的场景。
- 高级数据结构:比如在红黑树、B 树中,我们需要访问节点的父节点,这可以通过在节点中保存一个指向父节点的引用来实现,类似于双向链表。
- 浏览器历史:在网页浏览器中,当用户点击前进或后退按钮时,浏览器需要知道用户访问过的前一个和后一个网页。双向链表的特性使得这种操作变得简单。
- LRU 算法:在缓存淘汰(LRU)算法中,我们需要快速找到最近最少使用的数据,以及支持快速添加和删除节点。这时候使用双向链表就非常合适。
环形链表常用于需要周期性操作的场景,比如操作系统的资源调度。
- 时间片轮转调度算法:在操作系统中,时间片轮转调度算法是一种常见的 CPU 调度算法,它需要对一组进程进行循环。每个进程被赋予一个时间片,当时间片用完时,CPU 将切换到下一个进程。这种循环操作可以通过环形链表来实现。
- 数据缓冲区:在某些数据缓冲区的实现中,也可能会使用环形链表。比如在音频、视频播放器中,数据流可能会被分成多个缓冲块并放入一个环形链表,以便实现无缝播放。
4.3 列表(list)
- 列表是一个抽象出来的概念,是元素的有序集合,支持元素增、删、查、改、遍历。
- 列表可以用数组 / 链表实现。
- 链表天然就是一个列表,增、删、查、改、遍历都有,且可以灵活扩容。
- 数组可以看作一个具有长度限制的列表,虽然也能增、删、查、改、遍历,但是长度不可变。
- c语言中没有动态数组。C++、C#、Python、Java都支持动态数组。
4.3.1 列表的基操
调用内置函数实现
4.3.2 列表的简单实现
- 初始容量
- 数据记录
- 扩容机制
#include <stdio.h>
// 列表结构体
typedef struct
{
int *arr; // 数组
int capacity; // 列表容量
int size; // 列表大小
int extendRatio; // 列表每次扩容倍数
} Mylist;
// 构造函数
Mylist *newMylist()
{
Mylist *nums = (int *)malloc(sizeof(Mylist));
nums->capacity = 10;
nums->arr = (int *)malloc(sizeof(int) * nums->capacity);
nums->size = 0;
nums->extendRatio = 2;
return nums;
}
// 析构函数
void delMylist(Mylist *nums)
{
free(nums->arr);
free(nums);
}
// 获取列表容量
int capacity(Mylist *nums)
{
return nums->capacity;
}
// 获取列表大小
int size(Mylist *nums)
{
return nums->size;
}
// 列表转换为数组
int *toArray(Mylist *nums)
{
return nums->arr;
}
// 访问元素
int get(Mylist *nums, int index)
{
assert(index >= 0 && index < nums->size);
return nums->arr[index];
}
// 更新元素
void set(Mylist *nums, int index, int newNum)
{
assert(index >= 0 && index < nums->size);
nums->arr[index] = newNum;
}
// 列表扩容
void extendCapacity(Mylist *nums)
{
// 分配空间
int newCapacity = capacity(nums) * nums->extendRatio;
int *extendNums = (int *)malloc(sizeof(int) * newCapacity);
int *oldArr = nums->arr;
// 旧数组复制到新数组
for (int i = 0; i < size(nums); i++)
{
extendNums[i] = oldArr[i];
}
// 释放旧数据
free(oldArr);
// 更新数据到原数组
nums->arr = extendNums;
nums->capacity = newCapacity;
}
// 在尾部添加元素
void addLast(Mylist *nums, int newNum)
{
if (size(nums) == capacity(nums))
{
extendCapacity(nums);
}
nums->arr[size(nums)] = newNum;
nums->size++;
}
// 在中间插入元素
void insert(Mylist *nums, int index, int newNum)
{
assert(index >= 0 && index <= size(nums));
if (size(nums) == capacity(nums))
{
extendCapacity(nums);
}
// index后面的元素后移一位
for (int i = size(nums); i > index; i--)
{
nums->arr[i] = nums->arr[i - 1];
}
nums->arr[index] = newNum;
nums->size++;
}
// 删除元素
int removeItem(Mylist *nums, int index)
{
assert(index >= 0 && index < size(nums));
int removedNum = nums->arr[index];
// index以及后面的元素前移一位
for (int i = index; i < size(nums) - 1; i++)
{
nums->arr[i] = nums->arr[i + 1];
}
nums->size--;
return removedNum;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号