计算机视觉--图像到图像的映射

一、原理

单应性变换：

        是将平面内的一个点映射到另一个平面内的二维投影变换，单应性变换矩阵是一个3*3的矩阵，具有8个自由度，第三行第三列，也就是最后一个值为1。单应性矩阵可以由两幅图像中对应点计算出来。

公式推导可以参考：https://blog.csdn.net/limmmy/article/details/88662042

仿射变换：

        一种二维坐标到二维坐标之间的线性变换（相同平面），它保持了二维图形的“平直性”（直线经过变换之后依然是直线）和“平行性”（二维图形之间的相对位置关系保持不变，平行线依然是平行线，且直线上点的位置顺序不变），但是角度会改变。任意的仿射变换都能表示为乘以一个矩阵(线性变换)，再加上一个向量 (平移) 的形式。单应性变换有8个自由度，仿射有6个自由度。

二、homography.py文件的内容

import numpy as np
from numpy import *
from matplotlib.pyplot import *
from scipy import ndimage
from PIL import Image
def normallize(points):
    """在齐次坐标意义下，对点集进行归一化，是最后一行为1"""
    for row in points:
        row /= points[-1]
    return points

def make_homog(points):
    """将点集（dim×n的数组）转换为齐次坐标表示"""

    return np.vstack((points,np.ones((1, points.shape[1]))))

def H_from_points(fp, tp):
    """使用线性DLT方法，计算单应性矩阵H，使fp映射到tp。点自动进行归一化"""

    if fp.shape != tp.shape:
        raise RuntimeError('number of points do not match')

    # 对点进行归一化（对数值计算很重要）
    # --- 映射起始点 ---
    m = np.mean(fp[:2], axis=1)
    maxstd = max(np.std(fp[:2], axis=1)) + 1e-9
    C1 = np.diag([1/maxstd, 1/maxstd, 1])
    C1[0][2] = -m[0]/maxstd
    C1[1][2] = -m[1]/maxstd
    fp = np.dot(C1,fp)
    
    # --- 映射对应点 ---
    m = np.mean(tp[:2], axis=1)
    maxstd = max(np.std(tp[:2], axis=1)) + 1e-9
    C2 = np.diag([1 / maxstd, 1 / maxstd, 1])
    C2[0][2] = -m[0] / maxstd
    C2[1][2] = -m[1] / maxstd
    tp = np.dot(C2, tp)
    
    # 创建用于线性方法的矩阵，对于每个对应对，在矩阵中会出现两行数值
    nbr_correspondences = fp.shape[1]
    A = np.zeros((2 * nbr_correspondences, 9))
    for i in range(nbr_correspondences):
        A[2*i] = [-fp[0][i], -fp[1][i],-1,0,0,0,
                  tp[0][i]*fp[0][i],tp[0][i]*fp[1][i],tp[0][i]]
        A[2*i+1] = [0,0,0,-fp[0][i],-fp[1][i],-1,
                    tp[1][i]*fp[0][i],tp[1][i]*fp[1][i],tp[1][i]]
        
    U,S,V = np.linalg.svd(A)
    H = V[8].reshape((3,3))
    
    #反归一化
    H = np.dot(np.linalg.inv(C2),np.dot(H,C1))
    
    #归一化，然后返回
    return H / H[2,2]

def Haffine_from_points(fp, tp):
    """计算H仿射变换，使得tp是fp经过仿射变换H得到的"""

    if fp.shape != tp.shape:
        raise RuntimeError('number of points do not match')
        
    # 对点进行归一化（对数值计算很重要）
    # --- 映射起始点 ---
    m = np.mean(fp[:2], axis=1)
    maxstd = max(np.std(fp[:2], axis=1)) + 1e-9
    C1 = np.diag([1/maxstd, 1/maxstd, 1]) 
    C1[0][2] = -m[0]/maxstd
    C1[1][2] = -m[1]/maxstd
    fp_cond = np.dot(C1,fp)
    
    # --- 映射对应点 ---
    m = np.mean(tp[:2], axis=1)
    C2 = C1.copy() # 两个点集，必须都进行相同的缩放
    C2[0][2] = -m[0]/maxstd
    C2[1][2] = -m[1]/maxstd
    tp_cond = np.dot(C2,tp)
    
    # 因为归一化后点的均值为0，所以平移量为0
    A = np.concatenate((fp_cond[:2],tp_cond[:2]), axis=0)
    U,S,V = np.linalg.svd(A.T)
    
    # 如Hartley和Zisserman著的Multiplr View Geometry In Computer,Scond Edition所示，
    # 创建矩阵B和C
    tmp = V[:2].T
    B = tmp[:2]
    C = tmp[2:4]
    
    tmp2 = np.concatenate((np.dot(C,np.linalg.pinv(B)),np.zeros((2,1))), axis=1) 
    H = np.vstack((tmp2,[0,0,1]))
    
    # 反归一化
    H = np.dot(np.linalg.inv(C2),np.dot(H,C1))
    
    return H / H[2,2]

def image_in_image(im1, im2, tp):
    """使用仿射变换将im1放置在im2上，使im1图像的角和tp尽可能的靠近
        tp是齐次表示的，并且是按照从左上角逆时针计算的"""
    
    # 扭曲的点
    m,n = im1.shape[:2]
    fp = array([[0,m,m,0],[0,0,n,n],[1,1,1,1]])
    
    # 计算仿射变换，并且将其应用于图像im1中
    H = Haffine_from_points(tp,fp)
    im1_t = ndimage.affine_transform(im1,H[:2,:2],
                    (H[0,2],H[1,2]),im2.shape[:2])
    alpha = (im1_t > 0)
    
    return (1-alpha)*im2 + alpha*im1_t

三、图像扭曲

        对图像块应用仿射变换，我们将其称为图像扭曲（或者仿射扭曲）。该操作不仅经常在计算机图形学中，而且经常出现在计算机视觉算法总。扭曲的操作可以使用SciPy工具包中的ndimage包来简单完成。实验代码实现如下：

im = array(Image.open('jf3.jpg').convert('L'))
H = array([[1.4,0.05,-100],[0.05,1.5,-100],[0,0,1]])
im2 = ndimage.affine_transform(im, H[:2,:2],(H[0,2],H[1,2]))
 
gray()
subplot(121)
imshow(im)
axis('off')
subplot(122)
imshow(im2)
axis('off')
show()

运行结果：

                                    

 

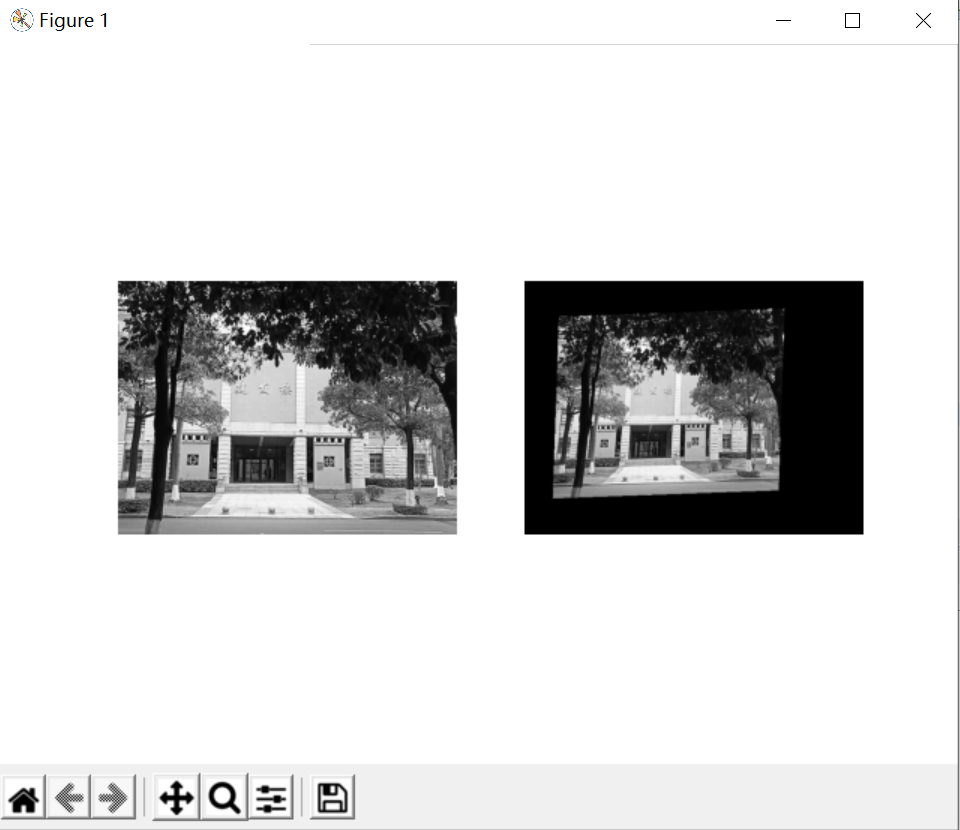
         作图为拍摄的建发楼原图，右图是经过仿射变换得到的图片，没有映射到的像素点填充为0，为黑色，可以看见经过仿射变换后图片的角度发生了变化。

四、图像中的图像

        仿射扭曲的一个简单例子是，将图像或者图像的一部分放置在另一幅图像中，是的他们能够和指定的区域或者标记物对齐。代码实现如下：

im1 = array(Image.open('dy-ja1.jpg').convert('L'))
im2 = array(Image.open('dy-ja2.jpg').convert('L'))

gray()
subplot(131)
imshow(im1)
axis('equal')
axis('off')
subplot(132)
imshow(im2)
axis('equal')
axis('off')

# tp是映射目标位置
tp = array([[144, 272, 266, 141], [216, 216, 272, 269], [1, 1, 1, 1]])

im3 = image_in_image(im1, im2, tp)
subplot(133)
imshow(im3)
axis('equal')
axis('off')
show()

运行结果：

        im1（第一张图）是道远楼的图片，im2（第二张图）是建安楼，这段代码是将im1扭曲映射到im2指定的位置中，以替换楼房名称，想象中是无缝连接，事实是有色差，获取tp目标坐标是先显示im2图片，然后鼠标放至目标位置，从右下角取得xy坐标值