斐波那契堆——算法导论(26)

1. 写在前面

在很久之前学习过堆这种数据结构。这次再来学习一种比较特别的“堆”——斐波那契堆。下文首先会介绍斐波那契堆的结构，然后会介绍在其上的操作，最后再分析这些操作的效率，以及一些理论的证明。

2. 结构

斐波那契堆是一系列具有最小堆序的有根树的集合，即斐波那契堆中的每棵树均遵循最小堆性质。

所谓最小堆性质是指：树中的每个结点的关键字大于或等于它的父结点（若存在）的关键字。具有最小堆性质的堆，我们称之为最小堆。

举个栗子，下图便是一个斐波那契堆：

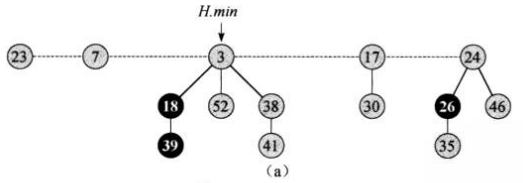
从图中可以看出，它是由5个最小堆组成的，每个堆的根节点以链表的形式相互连接。

以上便是斐波那契堆的基本结构，除此之外，它还具有如下特点：

1. 每个最小堆中的每一个结点$x$包含一个指向它父结点的指针$x.p$和一个指向它某一孩子结点的指针$x.child$；
2. 每个结点$x$的所有孩子被链接成一个环形的双向链表（称为$x$的孩子链表(child list)），即$x$的每一个孩子$y$均有指针$y.left, y.right$分别指向它的左兄弟和右兄弟。特别地，如果孩子链表中只有一个结点，则$y.left, y.right$指向自己，即$y.left = y.right = y$。
3. 每个结点$x$还具有另外两个属性：一个是$x.degree$，表示自己孩子的数目。另一个是一个布尔类型的属性$x.mark$，表示结点$x$自从上一次成为某一个结点的孩子后，是否失去过孩子。
4. 对于一个给定的斐波那契堆$H$，它有一个属性$min$，指向具有最小关键字的最小堆的根结点（称为斐波那契堆的最小结点(minimum node)）。
5. 所有组成斐波那契堆的最小堆的根结点也链接形成一个双向链表，它称为斐波那契堆的根链表(root list)。

因此，若要完整的把之前图中所示的斐波那契堆的的结点关系画出来，结果如下：

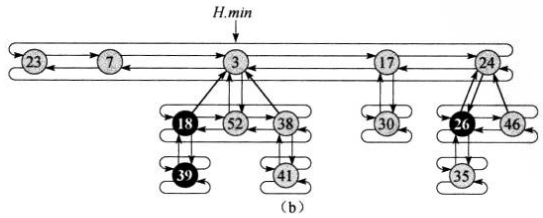
3. 操作

斐波那契堆支持可合并堆操作。所谓可合并堆（mergeable），是指支持以下5种操作的一种数据结构：

1. make-heap()：创建和返回一个新的不含任何元素的堆；
2. insert(H, x)：将元素$x$插入堆$H$中；
3. minimum(H)：返回堆H中具有最小关键字的结点；
4. extract-min(H)：从堆H中删除具有最小关键字的结点并返回；
5. union($H_1, H_2$)：创建并返回一个包含堆$H_1$和堆$H_2$的中所有元素的新堆。

除此之外，斐波那契堆还支持以下两种操作：

1. decrease-key(H, x, k)：将堆H中元素x的关键字赋予新值k（k不大于当前的关键字）。
2. delete(H, x)：从堆中删除元素x。

下面用Java来实现斐波那契堆。

3.1 创建一个新的斐波那契堆

首先定义出斐波那契堆的数据结构：

/**
 * 斐波那契堆
 */
public class FibonacciHeap<T extends Comparable<T>> {
    private int size; // 堆中元素的个数
    private Node<T> minNode; // 指向堆中的最小元素
    
  	/**
  	* 堆节点 
  	*/
    private static class Node<T extends Comparable> {
        Node<T> parent;
        List<Node<T>> children;
        Node<T> left; // 左兄弟
        Node<T> right; // 右兄弟
        int degree;
        boolean mark;
        T data;
        
        Node(T data) {
            this.data = data;
            left = this;
            right = this;
        } 
    }
}

其中Node静态内部类是来封装我们插入的数据和维护数据之间的关联关系，在学习基本数据结构链表或者二叉树时应该接触过，接下来实现各操作。

3.2 insert

插入结点的算法很简单，就是将结点插入根链表中，然后更新最小根节点（minNode）。更新的逻辑是：若此时堆是空的，直接将minNode指向插入的节点即可；若堆非空，我们将节点插入到最小节点的左边，再重新判断最小节点。

下面Java实现给出代码：

/**
 * 插入数据
 * @param data
 */
public void insert(T data) {
    if (data == null) {
        throw new NullPointerException("不能插入null值");
    }
    Node<T> node = new Node<>(data);
    if (minNode == null) {
        minNode = node;
    } else {
        node.insertLeftOf(minNode);
        if (data.compareTo(minNode.data) < 0)
            minNode = node;
    }
    size++;
}

insertLeftOf方法用于将某节点插入到指定节点的左边，它定义在Node内部类中，如下：

private static class Node<T extends Comparable<T>> {
    // 省略成员变量以及其他方法...
    
    private void insertLeftOf(Node<T> node) {
        left = node.left;
        right = node;
        node.left.right = this;
        node.left = this;
    }	
}

3.3 minimum

minimum方法用于返回堆中具有最小关键字的结点。由于我们用一个叫做minNode的变量指向堆中的最小节点，因此minimum过程只需返回该变量封装的数据即可：

/**
 * 获取最小的数据
 * @return 最小的数据
 */
public T minimum() {
    return minNode == null ? null : minNode.data;
}

3.4 extractMin

extractMin方法用于删除堆中具有最小关键字的结点，并返回。extractMin是斐波那契堆中复杂的操作（其实也并不复杂）。它分以下几个操作步骤完成：

1. 首先把最小节点的所有子节点移动到根链表中，具体移动到根链表中的哪个位置不做要求；接着从根链表中删除最小节点。
2. 判断原先堆中是否只有一个元素，若是，那么操作到此结束；否则继续下一步。
3. 将根链表中度数相同的节点进行合并。合并的方式是将两个度数相同的节点中数据较大那个从根链表中移除，挂载到较小的那个节点上，成为其子节点。

步骤3可能会产生疑惑。下面用一个实际的例子帮助理解。比如下图是给出的一个斐波那契堆，我们要对其进行extractMin操作。

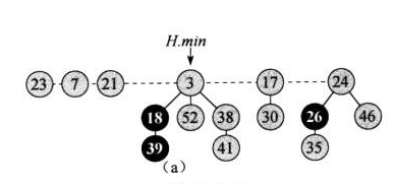
第一步：将最小节点（3）的子节点（18， 52， 38）移动到根链表中（这里采取将它们移到最小节点的左边），然后从根链表中移除最小节点。删除后暂时将minNode指针指向被删除的最小节点的右兄弟节点。这样得到下图：

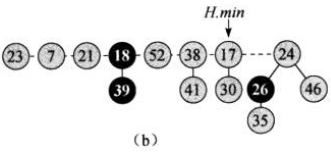
第二步：显然判断的结果是要执行第三步。

第三步：合并根链表中度数相同的节点。显然我们需要统计根链表中每个节点的度数，于是选用一个数组来保存统计结果，并且约定，该数组存放的是节点的指针，而数组下标的值表示对应节点的度数；接下来可以开始统计合并了。从min节点开始，向右遍历根链表。在遍历的每轮中，首先以当前遍历节点的度数为下标去数组中查找，若该位置是空的，说明遍历到现在还没有出现过该度数的节点，直接将当前节点存放到数组中；若该下标对应的位置不是空的，说明当前节点和数组中该下标对应的位置中的节点度数相同，因此要合并这两个节点。

回到上面的例子，我们从临时最小根节点（17）开始从左往右遍历根链表。第一轮，节点17的度数为1，而数组中下标为1的位置为空，因此，直接将节点的指针（引用）存放到数组的1号位置：

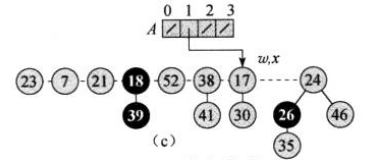
接着遍历到节点24，其度数为2，2号位置也是空的，直接将节点24放到2号位置：

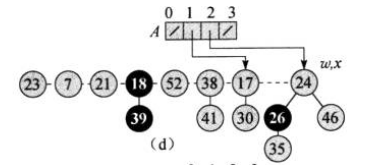
下一轮遍历需要回到链表的头部，即到了节点23，以其度数为下标的位置是空的，操作同上：

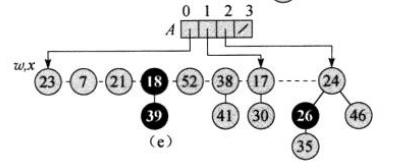
再接下来是节点7，注意其度数为0，而数组中0号位置已经有了节点23，这说明它们的度数都为0，需要合并。合并时，比较它们数据的大小，显然7小于23，因此将23挂到7下作为子节点：

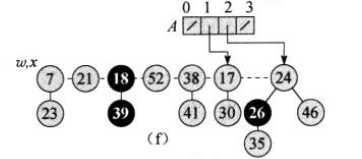
注意，在合并后节点7的度数加了1，变为了1，需要继续判断数组的1号位置，1号位置存放的是节点17，因此需要继续合并节点7和节点17。再之后的工作就和上述一致了，这里就不在一一赘述了，直接给出每步操作后的图：

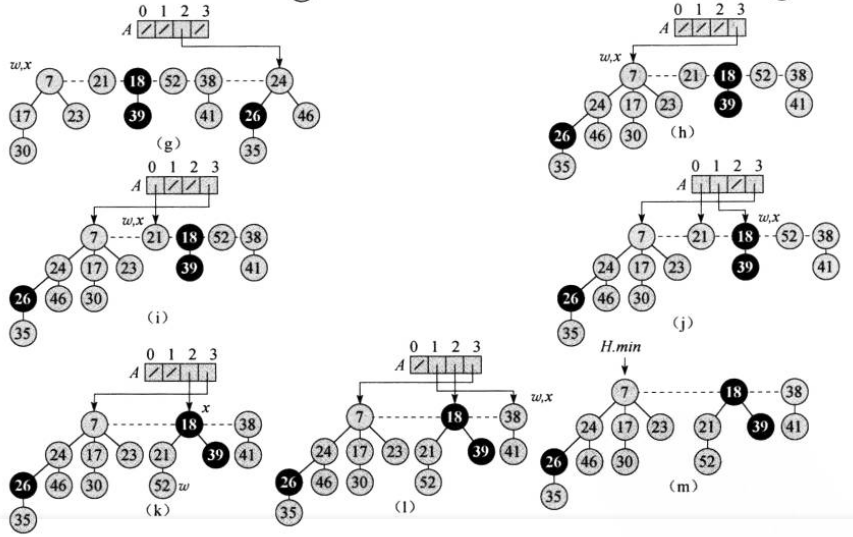
下面给出该 操作的Java代码：

/**
 * 取出最小数据
 *
 * @return 若堆不为空，返回堆中最小数据；否则返回空。
 */
public T extractMin() {
    if (minNode == null) {
        return null;
    }
    T min = minNode.data;
    if (minNode.children != null) {
        for (Node<T> child : minNode.children) {
            // 将子节点插入到根链表中
            child.insertLeftOf(minNode);
            child.parent = null;
        }
    }
    minNode.removeSelfFromSiblings();
    if (minNode.right == minNode) {
        minNode = null;
    } else {
        minNode = minNode.right;
        consolidate();
    }
    size--;
    return min;
}

/**
 * 合并根链表，使每一个根链表都有不同的度数。
 */
private void consolidate() {
    Node<T>[] array = new Node[(int) (Math.log(size) / LOG_Φ)];
    Node<T> endNode = minNode.left;
    Node<T> currentNode = minNode.left, nextNode = minNode;
    do {
        currentNode = nextNode;
        nextNode = currentNode.right;
        Node<T> max = null, min = currentNode;
        while ((max = array[min.degree]) != null) {
            // 存在相同度数的根节点，将较大的节点挂载到较小的节点上（作为较小的节点的子节点）
            if (max.data.compareTo(min.data) < 0) {
                Node<T> temp = min;
                min = max;
                max = temp;
            }
            max.removeSelfFromSiblings();
            min.addChild(max);
            array[min.degree - 1] = null;
        }
        array[min.degree] = min;
    } while (currentNode != endNode);
    // 下面从根列表中重新选出最小节点
    minNode = null;
    for (Node<T> node : array) {
        if (node == null) {
            continue;
        }
        if (minNode == null || node.data.compareTo(minimum()) < 0) {
            minNode = node;
        }
    }
}

private static class Node<T extends Comparable<T>> {
    /**
     * 将自己从所在的链表中移除
     */
	private void removeSelfFromSiblings() {
    		left.right = right;
    		right.left = left;
	}
}

以上其实还隐藏着一个问题：我们需要为统计数组分配多大的长度？由于我们把数组的下标作为节点的度数，因此数组的长度必须不小于根链表中节点的最大度数（设为$D$）。显然$D$是小于堆的总节点数size的，但更加紧确地，我们可以证明$D\le log_\theta$size，这里$\theta$是黄金分割率，为$(1 + \sqrt5) / 2=1.61803...$，这个在最后证明。

3.5 union

union操作比较简单，只需要将待合并的两个斐波拉契堆的根链表连起来，重新计算size和minNode即可。

/**
 * 合并俩FibonacciHeap
 */
public static <T extends Comparable<T>> FibonacciHeap<T> union(FibonacciHeap<T> heap1, FibonacciHeap<T> heap2) {
    FibonacciHeap<T> heap = new FibonacciHeap<T>();
    heap.size = heap1.size + heap2.size;
    heap.minNode = heap1.minNode;
    if (heap1.minNode == null || heap2.minNode != null && heap2.minNode.data.compareTo(heap1.minNode.data) < 0) {
        heap.minNode = heap2.minNode;
    }
    return heap;
}

3.6 decrease和delete

decrease操作即为将某个节点的值(data字段)减小为某一个值。可以想象，将一个节点的值减小和其子节点的值是不冲突的，但可能和其父节点的值产生冲突。为解决这一冲突，我们可以将修改的这个节点移动到根链表中，然后再做一个“级联剪切”工作，最后重新选出最小节点。具体操作过程以伪代码的形式给出：

感兴趣的童鞋可以自己实现一下，这里就不给出具体实现了。

同样下面贴出一个列子：

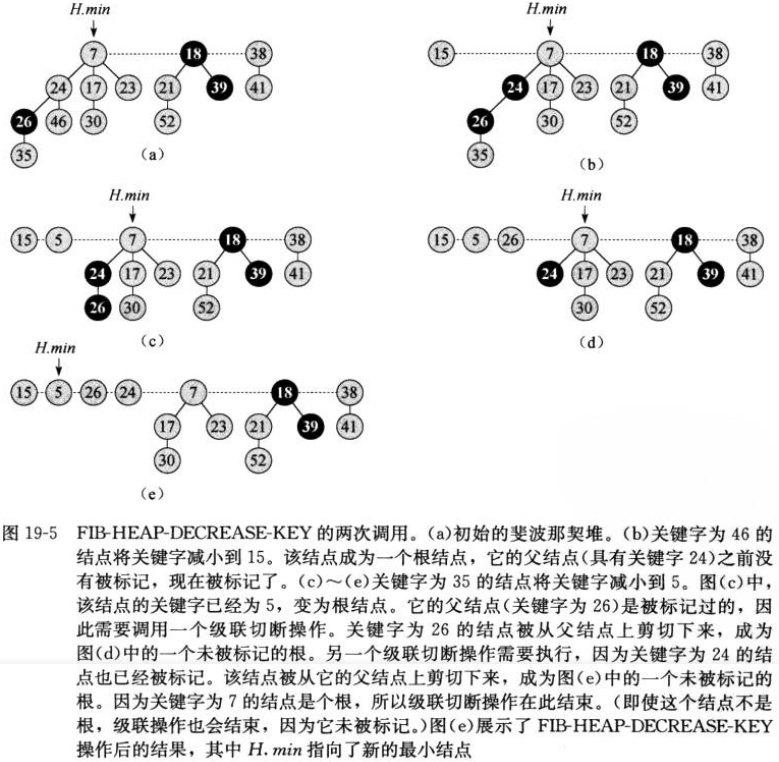
有了减小节点数据的操作，实现删除节点的功能就简单了。只需要将要删除的节点的值减到无穷小，这样minNode指针就自然地指向到了它，接着调用之前实现的extractMin方法就能将数据去除。

贴出伪代码，同样不实现了：

以上便是斐波那契堆支持的主要操作，下面来分析各个操作的时间效率。

4. 效率

4. 1 摊还分析

下面对斐波那契堆进行摊还分析。之所以关注摊还分析的结果，而不是关注每一个单独的操作的效率，是因为斐波那契堆的优势在于其各个操作的摊还代价较低。我们用势能法来分析摊还代价。

首先定义势函数$\theta(H) = t(H) + 2m(H)$，其中$t(H)$表示堆中根链表中节点的个数；$m(H)$表示节点中已标记的节点的节点的数目。显然初始时$\theta$为0，并且在之后的任意时刻势$\theta$都是不为负的，因此对于某一操作序列来说，总的摊还代价的上界就是其总的实际代价的上界。

1. 对于insert操作，实际代价为$O(1)$，势变化为1，我们可以很容易计算出其摊还代价为$O(1) + 1 = O(1)$；
2. 对于minimum操作，摊还代价就等于实际代价为$O(1)$；
3. 对于union操作，实际代价为$O(1)$，势变化为0，因此摊还代价为$O(1)$；
4. 对于extractMin操作，实际代价为$O(D(H))$，其中$D(H)$为堆H中根链表中节点的最大度。（之前在介绍extractMin操作时，其实有一个问题没有解决，就是那个用来记录度是否重复的数组的长度问题，即这里的$D(H)$。我们之后再介绍计算$D(H)$的方法，这里先直接给出它的上界为$O(ln n)$。）势变化为$O(D(H))$，因此摊还代价为$O(H)$。
5. 对于decreaseKey操作，其摊还代价至多为$O(1)$；而delete方法的摊还代价为$O(ln n)$。

4. 2 关于最大度数的界

要证明

$D(H) \leq \lfloor log_\Phi n \rfloor$，其中$\Phi$为黄金分割率$(\sqrt 5 + 1) / 2 = 0.618$。

需要先证明如下几个引理。

引理1. 设x是斐波那契堆中的任意节点，并假定$x.degree = k$。用$y_1, y_2, ..., y_k$表示x的k个孩子，它们是以链入x的顺序排列的，则$y_1.degree \geq 0$，且对于$i = 1, 2, ..., k$，有$y_i.degree \geq i - 2$。

证明：显然$y_1.degree \geq 0$；对于$i \geq 2$，当$y_i$被链接为$x$的孩子时，$x$已经有$y_1, y_2, ... y_{i-1}$ $i-1$个孩子，因此此时一定有$x.degree \geq i-1$，并且此时一定有$x.degree = y_i.degree$（这是进行合并操作的前提），而且在合并之后，$y_i$一定至多失去一个孩子（若失去两个孩子，它将被从x中剪切掉(cascading-cut)），得证。

引理2. 对于所有整数$k \geq 0$，$F_{k+2} = 1 + \sum_{i = 0} ^ kF_i$，其中$F_k$为斐波那契数列中的第k个数，即

$$F_k = \begin{cases} 0 & k = 0,\\ 1 & k = 1, \\ F_{k-1} + F_{k-2} & k \geq 2 \end{cases}$$

证明：整个证明比较简单，用数学归纳法就能搞定，此处略。

引理3. 对于所有整数$k \geq 0$，斐波那契数列的第$k+2$个数满足$F_{k+2} \geq \Phi ^k$。

证明：同样是数学归纳法证明，略。

引理4. 设x是斐波拉契堆中的任意节点，并设$k = x.degree$，则有$size(x) \geq F_{x+2} \geq \Phi ^k$，其中 $\Phi = (\sqrt 5 + 1) / 2,size(x)$表示以x为根的子树中包括x本身在内的节点个数。

证明：设$s_k$表示斐波那契堆中度数为$k$的任意节点$x$的最小可能size，一般地，$s_0=1, s_1=2$ 。显然，$s_k$随$k$单调递增。设$size(x)$表示以$x$为根节点的子树的节点个数（包括$x$自身）。显然$size(x) \ge s_k$。设$d(x)$表示节点$x$的度数。

对于任意节点$x$，记$d(x) = k$，用$y_1, y_2, ..., y_k$表示x的k个孩子，它们是以链入x的顺序排列的，将$x$本身和其第一个孩子$y_1$单独计数，则有：

$$size(x) \ge s_k \ge 2 +\sum_{i=2}^k s_{d(y_i)} \ge 2 + \sum_{i=2}^k s_{i-2}$$

其中最后一个不等式由引理1和$s_k$的单调递增性得到。

有了以上不等式的基础，我们用数学归纳法可证明$s_k \ge F_{k+2}$（其中还用到了引理2），再由引理3，最终有：$size(x) \geq F_{x+2} \geq \Phi ^k$.

最终，根据引理4，有$size \ge size(x) \ge \Phi ^k$，于是我们可推出$k \le log_\Phi n$，这表示任意节点的最大度数$D$为$O(lgn)$。