堆排序与优先队列——算法导论(7)
1. 预备知识
1.1 基本概念
先来介绍堆的概念。
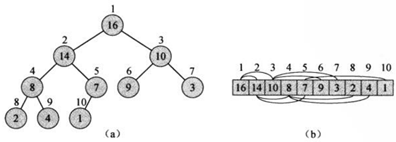
如图(a),(二叉)堆是一个近似的完全二叉树。树中的每一个结点对应数组中的一个元素。除了最底层外,该树是完全充满的,而且从左向右填充。
堆可以用数组来实现,如图(b)所示。堆中的节点在数组中,按树广度优先遍历的结果依次排列。在这种实现方式下,堆应该包含两个基本属性:length,给出数组的长度;heap-size,表示堆中有多少个元素。
由于堆的这种特殊的结构,我们可以很容易根据一个结点的下标i计算出它的父节点、左孩子、右孩子的下标。计算公式如下:
parent(i) = i / 2;
left-child(i) = 2i;
right-child(i) = 2i + 1;
二叉堆有两种形式:最大堆、最小堆。在这两种形式中,结点的值都要满足以上给出的堆的性质。二者的差异在于:在最大堆中,父节点的值均大于子节点(根节点因为没有父节点,所以不要求在内);最小堆相反。
在用途上,最大堆通常用在堆排序算法中;最小堆通常用于构建优先队列。
我们定义,堆中每个结点的高度为该结点到叶结点最长简单路径上,边的数目。而堆的高度,就为根结点的高度。
1.2. 维护堆的性质
我们用 MAX-HEAPIFY 函数来维护以下标 i 为根结点的子树的最大堆性质(这里假定以下标left(i)为根结点的子树和以下标为right(i)为根结点的子树满足最大堆的性质)。MAX-HEAPIFY函数的输入为一个数组A和一个下标 i ,其思想是通过让 A[i] 的值在最大堆中“逐级下降”,从而使得以下标 i 为结点的子树重新遵循最大堆的性质。
1.3 建堆
我们可以用置底向上的方法,利用过程 MAX-HEAPIFY 把一个大小为 n=A.length 的数组A[1~n]转化为最大堆。原理很简单,就是从倒数第2层(为说明方便,我们把根结点叫做第1层,其子结点叫做第2层,依次类推)开始,调用MAX-HEAPFY方法,直至到根结点。算法描述如下:
可以用以前介绍的循环不变式(见算法基础——算法导论(1))去证明以上算法的正确性:
初始化:在第一次循环迭代之前,需要构建的堆只包含最底层元素,当然满足堆的性质(这被称为平凡最大堆)。
保持:假设循环迭代式在第i(1 ≤ i < A.length/2)次迭代时是成立的,即以下标为i的元素为根结点的子树满足最大堆的性质;当i = i + 1时,max-heapify方法的执行保证了,当以下标left(i)为根结点的子树和以下标为right(i)为根结点的子树满足最大堆的性质时,以下标i为根结点的子树满足最大堆的性质(这正是该方法的作用)。因此循环迭代式具有保持性。
终止:当循环终止时,根据保持性,需要构建的堆由初始化的只包含最底层元素,扩展为包含所有元素。
因此,算法正确。
2. 堆排序(heap-sort)
了解了以上的预备知识后,我们正式开始介绍堆排序。
下面给出堆排序算法:
简单地说,其原理是基于最大堆的根结点元素最大的性质。我们首先将待排序的数组构建为最大堆数组。然后遍历整棵树,每次遍历“取出”根结点,再调用 MAX-HEAPIFY 维护子树的最大堆性质,这样就能保证遍历时每次“取出”的元素是当前剩余元素中最大的。(“取出”不一定要真正的把元素从数组里取出,我们可以通过改变heap-size的值来达到此效果)
下面给出Java实现代码:
1 // 测试 2 public static void main(String[] args) { 3 int[] array = { 2, 1, 6, 3, 9, 7, 4, 0, 4 }; 4 heapSort(array); 5 printArray(array); 6 } 7 8 /** 9 * 堆排序 10 * @param array 11 */ 12 public static void heapSort(int[] array) { 13 buildMaxHeap(array); 14 int heapSize = array.length; 15 for (int i = array.length - 1; i > 0; i--) { 16 int temp = array[i]; 17 array[i] = array[0]; 18 array[0] = temp; 19 heapSize--; 20 maxHeapify(array, 0, heapSize); 21 } 22 } 23 24 /** 25 * 维护以index为根节点的树的最大堆性质 26 * 27 * @param array 28 * 堆数组 29 * @param index 30 * 要维护的结点 31 */ 32 public static void maxHeapify(int[] array, int index, int heapSize) { 33 int leftIndex = 2 * index + 1; 34 int rightIndex = 2 * index + 2; 35 int largeIndex; 36 if (leftIndex < heapSize && array[leftIndex] > array[index]) { 37 largeIndex = leftIndex; 38 } else { 39 largeIndex = index; 40 } 41 if (rightIndex < heapSize && array[rightIndex] > array[largeIndex]) { 42 largeIndex = rightIndex; 43 } 44 if (largeIndex != index) { 45 int temp = array[largeIndex]; 46 array[largeIndex] = array[index]; 47 array[index] = temp; 48 maxHeapify(array, largeIndex, heapSize); 49 } 50 } 51 52 /** 53 * 将array构建为最大堆数组 54 * 55 * @param array 56 */ 57 public static void buildMaxHeap(int[] array) { 58 int heapSize = array.length; 59 for (int i = (array.length - 2) / 2; i > -1; i--) { 60 maxHeapify(array, i, heapSize); 61 } 62 } 63 64 public static void printArray(int[] array) { 65 for (int i : array) { 66 System.out.print(i + ""); 67 } 68 System.out.println(); 69 }
结果:
3. 算法分析
我们按照main方法的执行顺序来逐步分析算法的时间代价。
① 先分析buildMaxHeap方法。要分析buildMaxHeap方法先要分析maxHeapify方法。
我们假设maxHeapify方法在每次执行时,都会进行执行递归操作,在最坏的情况(树的最底层恰好半满)下,子树的规模是原来的2/3。其他时间为常量θ(1);因此我们可以得到运行时间的递归式:
T(n) ≤T(2n/3)+θ(1),
可解得,T(n) = O(lgn),即maxHeapify方法的时间复杂度为O(lgn)。
我们对buildMaxHeap方法进行粗略估计,它会调用O(n)次maxHeapify方法,而其他时间为常量θ(1),因此buildMaxHeap方法总的时间复杂度为:O(nlgn)。
但是这个上界显然不是渐进紧确的。因为事实上maxHeapify方法时间与结点的高度有关,而且大部分结点的高度都很小。
我们可以利用如下性质得到一个紧确的上界:包含n个元素的堆的高度是[lgn]([]表示向下取整);高度为h的堆至多包含【n/2^(h+1)】(【】表示向上去整)。
我们设在高度为h的结点上运行maxHeapify方法的时间代价是O(h),那么buildMaxHeap方法的总时间代价可以表示为:
所以,buildMaxHeap的时间复杂度为O(n)。
②我们再分析heapSort中的for循环。for循环执行n-1次,而每次循环执行的时间复杂度为O(lgn),因此总的时间复杂度为O(nlgn)。
③ 其他运行时间为常量O(1)。
因此heapSort的时间复杂度为O(nlgn)。
4. 优先队列(priority queue)
这一小节我们关注:如何基于最大堆来实现最大优先队列(priority queue)。
4.1 什么是最大优先队列(priority queue)
最大优先队列(priority queue)是一种用来维护一组数据构成的集合S的数据结构。其中的每一个元素都有一个关键值(key)。一个最大优先队列支持以下操作:
① maximum(s):返回集合s中具有最大关键字(key)的元素;
② extractMax(s):去掉并返回集合s中具有最大关键字(key)的元素;
③ increaseKey(s, x, k):将元素x的值增加到k(假设k的值不小于x);
④ insert(s, x):把元素x插入集合s中,即s = s U x。
4.2 方法的实现
① maximum(s)的实现很简单,直接返回根结点:
② extractMax(s)的实现同样简单,在返回根结点之前,先将其从树中“摘掉”,将堆数组中的最后一个元素挂载到根结点,再执行maxHeapify方法维护最大堆性质:
③ increaseKey(s, x, k)的实现方式是将下标为x的结点的值修改为k后,不断的与其父结点的值相比较,直至最终找到合适的位置,使得满足最大堆性质:
④ insert(s, x)方法利用了increaseKey(s, x, k)方法。具体做法是,先将x赋一个非常小的值,然后调用increaseKey(s, x, k)方法修改x的值为k。
4.3 补充说明
以上方法的具体代码实现和时间代价分析就不给出了,与堆排序类似(实际上就是堆排序的应用推演)。
最大优先队列的应用应该是很广泛的。比如用于任务调度,我们可以用insert(s, x)方法来提交一个任务;用extractMax(s)方法来获取任务;而increaseKey(s, x, k)方法可以用来修改任务的优先级。
显然,最大优先队列里记录的只是需要存储的对象的句柄(handle),其具体表现形式依赖于具体的应用程序。
与最大优先队列相反的是最小优先队列,它的实现方式基本与最大优先队列一致(是相反的),它有着不同的应用场景,以后会给出。
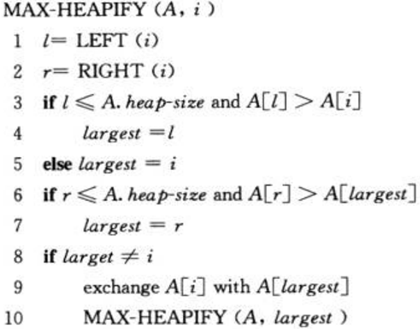
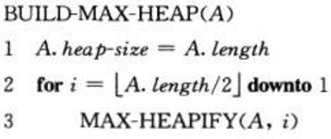

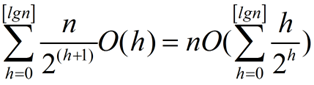



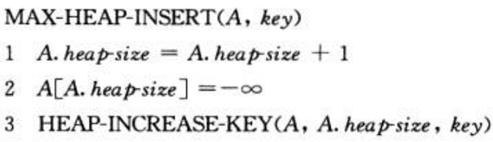

 浙公网安备 33010602011771号
浙公网安备 33010602011771号