第三次作业
第三次作业
姓名:丁星迪
邮箱:231275044@smail.nju.edu.cn
一. (25 points) 支持向量机
教材6.4节介绍了软间隔SVM的概念,被用来解决线性不可分情况下的SVM问题,同时也用来缓解SVM训练的过拟合问题。定义松弛变量 \(\pmb{\xi} = \{\xi_i\}_{i=1}^m\) , \(\xi_i > 0\) 表示样本 \(\pmb{x}_i\) 对应的间隔约束不满足的程度。使用下式来表示SVM问题:
该式显式地表示了分类器间隔 \(\rho\) 。基于这种约束形式的表示,可以定义两种形式的软间隔
第一种是绝对软间隔:
第二种是相对软间隔:
这两个软间隔分别使用 \(\xi_{i}\) 和 \(\rho \xi_{i}\) 衡量错分样本在间隔上的违背程度. 之后在优化问题中加入惩罚
使得不满足约束的样本数量尽量小 \((\xi_{i}\rightarrow 0)\)
- (5 points) 软间隔 SVM 通常采用相对软间隔, 请写出其原问题的形式 (形式中不包含 \(\rho\) ).
- (5 points) 请写出 \(p = 1\) 的情况下软间隔 SVM 的对偶问题
- (5 points) \(p = 1\) 的情况对应了 hinge 损失 \(\ell_{\text{hinge}}(x) = \max(0, 1 - x)\) ,请写出 \(p = 2\) 的情况下对应的损失函数.
- (10 points) 请推导 \(p = 2\) 的情况下软间隔 SVM 的对偶问题
解:
1.
软间隔 SVM 的“相对软间隔”约束为:
为了消除 \(\rho\) 并转化为标准的凸优化问题,我们采用 SVM 的标准推导技巧:令几何间隔与模长的乘积为 1(即固定函数间隔为 1)
令 \(\rho \| \boldsymbol {w} \| _ {2} = 1\),则 \(\rho = \frac{1}{\| \boldsymbol {w} \| _ {2}}\)。此时最大化 \(\rho\) 等价于最小化 \(\frac{1}{2}\| \boldsymbol {w} \| _ {2}^2\)
约束条件变为:
结合给定的惩罚项 \(C \sum \xi_i^p\),原问题形式如下(通常要求 \(\xi_i \geq 0\)):
2.
当 \(p=1\) 时,这是标准的软间隔 SVM。其对偶问题如下:
其中 \(\boldsymbol{\alpha} = (\alpha_1, \dots, \alpha_m)^\top\) 是拉格朗日乘子
3.
当 \(p=1\) 时,损失对应 Hinge Loss \(\ell(z) = \max(0, 1-z)\)
当 \(p=2\) 时,目标函数中的惩罚项为 \(\xi_i^2\)。根据约束 \(y_i(\boldsymbol{w}^\top \boldsymbol{x}_i + b) \geq 1 - \xi_i\) 且 \(\xi_i \geq 0\)(在 \(p=2\) 时非负约束往往非必须,因为平方项自会压制负值,但定义上仍保持一致),最优的 \(\xi_i\) 取值为 \(\max(0, 1 - y_i(\boldsymbol{w}^\top \boldsymbol{x}_i + b))\)
因此,对应的损失函数为平方合页损失 :
4.
当 \(p=2\) 时,原问题为:
引入拉格朗日乘子 \(\boldsymbol{\alpha} = \{\alpha_i\}_{i=1}^m \geq 0\) 对应分类间隔约束,\(\boldsymbol{\mu} = \{\mu_i\}_{i=1}^m \geq 0\) 对应松弛变量非负约束
1). 对 \(\boldsymbol{w}\) 求偏导:
2). 对 \(b\) 求偏导:
3). 对 \(\xi_i\) 求偏导:
由于 \(\xi_i, \alpha_i, \mu_i\) 的互补松弛条件以及 \(\xi_i\) 在 \(p=2\) 时若 \(\xi_i > 0\) 则 \(\mu_i=0\),若 \(\xi_i=0\) 则 \(\alpha_i+\mu_i=0 \Rightarrow \alpha_i=0\),我们可以简单地得到关系式(或直接代入):
注:在 L2-SVM 中,通常 \(\xi_i \geq 0\) 的约束是自然满足的(或 \(\mu_i\) 不影响对偶目标函数的最终形式,因为若 \(\alpha_i > 0\) 则 \(\xi_i > 0\)),可以简化为 \(\xi_i = \frac{\alpha_i}{2C}\)。即便保留 \(\mu_i\),在最大化过程中也会导致 \(\mu_i=0\)。
因此取 \(\xi_i = \frac{\alpha_i}{2C}\)
将求出的 \(\boldsymbol{w}, b, \xi_i\) 代回 \(L\):
我们可以将最后一项 \(-\sum \frac{\alpha_i^2}{4C}\) 合并到二次型中
于是对偶问题为:
其中 \(\delta_{ij}\) 是克罗内克函数(当 \(i=j\) 时为1,否则为0)。注意与 \(p=1\) 不同,这里 \(\alpha_i\) 没有上界 \(C\),只有非负约束
二. (30 points) 极大似然估计
本题以极大似然估计和最大后验估计的视角来研究线性回归模型.给定由 \(m\) 个样本组成的训练集 \(D = \{(x_{1},y_{1}),(x_{2},y_{2}),\ldots ,(x_{m},y_{m})\}\) ,其中 \(\pmb {x}_i = (x_{i1};x_{i2};\dots ;x_{id})\in \mathbb{R}^d\) 是第 \(i\) 个示例, \(y_{i}\in \mathbb{R}\) 是对应的实值标记.令 \(\pmb {X}\in \mathbb{R}^{m\times d}\) 表示整个训练集中所有样本特征构成的矩阵,并令 \(\pmb {y}\in \mathbb{R}^{m}\) 表示训练集中所有样本标记构成的向量.线性回归的目标是寻找一个参数向量 \(\pmb {w}\in \mathbb{R}^{d}\) ,使得在训练集上模型预测的结果和真实标记之间的差距最小.对于一个样本 \(\pmb{x}\) ,线性回归给出的预测为 \(\hat{y} = \pmb {w}\pmb{x}\) ,它与真实标记 \(y\) 之间的差距可以用平方损失 \((y - \hat{y})^{2}\) 来描述.在整个训练集上最小化损失函数的过程可以写成如下的优化问题:
- (10 points) 考虑这样一种概率观点: 样本 \(\pmb{x}\) 的标记 \(y\) 是从一个高斯分布 \(\mathcal{N}(\pmb{w}^{\top}\pmb{x},\sigma^{2})\) 中采样得到的. 这个高斯分布的均值由样本特征 \(\pmb{x}\) 和模型参数 \(\pmb{w}\) 共同决定, 而方差是一个额外的参数 \(\sigma^{2}\) . 这个观点实际上对应了这样一种数据生成过程: 样本的特征是从某个分布 \(p(\pmb{x})\) 中采样得到的, 而样本的“真实”标记 \(\hat{y}\) 是线性依赖于样本特征 \(\pmb{x}\) 的, 即 \(\hat{y} = \pmb{w}^{\top}\pmb{x}\) . 但是, 在采集标记时, 由于种种原因, 实际观测到的标记 \(y\) 比真实标记 \(\hat{y}\) 多出一个高斯噪声 \(\epsilon \sim \mathcal{N}(0,\sigma^{2})\) , 即 \(y = \hat{y} + \epsilon\) . 这种现象在实际的回归问题中是很常见的, 因为回归问题的标记是实数, 各种传感器、仪表等在测量实数值时总会出现一些误差. 基于这种概率观点, 就可以基于观测数据对高斯分布中的参数 \(\pmb{w}\) 做极大似然估计了. 请证明: \(\pmb{w}\) 的极大似然估计结果 \(\pmb{w}_{\mathrm{MLE}}\) 与式 (2) 中的 \(\pmb{w}^{*}\) 相等;
证:
考虑观测数据服从高斯分布的假设:对于每个样本 \(i\),\(y_i \sim \mathcal{N}(\boldsymbol{w}^\top \boldsymbol{x}_i, \sigma^2)\),且观测独立。似然函数为:
取对数似然:
极大化 \(\ell(\boldsymbol{w})\) 等价于最小化 \(\sum_{i=1}^m (y_i - \boldsymbol{w}^\top \boldsymbol{x}_i)^2 = \|\boldsymbol{Xw} - \boldsymbol{y}\|_2^2\)。因此,\(\boldsymbol{w}_{\mathrm{MLE}} = \arg\min_{\boldsymbol{w}} \|\boldsymbol{Xw} - \boldsymbol{y}\|_2^2 = \boldsymbol{w}^*\)
- (5 points) 上一题显示出极大似然估计容易过拟合, 一种常见的解决办法是采用最大后验估计. 延续第一小问的思路, 在概率建模下对参数 \(\pmb{w}\) 做最大后验估计. 为此, 引入参数 \(\pmb{w}\) 上的先验 \(p(\pmb{w}) = \mathcal{N}(\mathbf{0}, \lambda \pmb{I})\) . 其中, 均值 \(\mathbf{0}\) 是 \(d\) 维的全 0 向量, \(\pmb{I}\) 是 \(d\) 维单位矩阵, \(\lambda > 0\) 是一个控制方差的超参数 (因为 \(\lambda\) 是模型参数分布的参数, 所以称为超参数). 现在, 请推导对 \(\pmb{w}\) 做最大后验估计的目标函数;
解:
后验分布 \(p(\boldsymbol{w}|D) \propto p(D|\boldsymbol{w}) p(\boldsymbol{w})\),其中 \(p(\boldsymbol{w}) = \mathcal{N}(\mathbf{0}, \lambda \boldsymbol{I})\)。对数后验为:
其中 \(\log p(D|\boldsymbol{w}) = -\frac{1}{2\sigma^2} \|\boldsymbol{Xw} - \boldsymbol{y}\|_2^2 + C_1\)、\(\log p(\boldsymbol{w}) = -\frac{1}{2\lambda} \|\boldsymbol{w}\|_2^2 + C_2\)。最大后验估计的目标函数为:
- (5 points) 沿着上一小问的思路, 尝试给参数 \(\boldsymbol{w}\) 施加一个拉普拉斯先验. 首先介绍拉普拉斯分布:
由参数 \(\mu, \lambda\) 确定的一元拉普拉斯分布的概率密度函数为:
为了方便地定义参数 \(\pmb{w}\) 上的拉普拉斯先验,假设参数 \(\pmb{w}\) 的 \(d\) 个维度之间是独立的,且每一维都服从均值为0的一元拉普拉斯分布,即:
请推导对 \(\pmb{w}\) 做最大后验估计的目标函数;
解:
拉普拉斯先验 \(p(\boldsymbol{w}) = \prod_{j=1}^d \frac{1}{2\lambda} \exp\left( -\frac{|w_j|}{\lambda} \right)\),对数先验 \(\log p(\boldsymbol{w}) = - \frac{1}{\lambda} \|\boldsymbol{w}\|_1 + C\)。结合对数似然,最大后验估计的目标函数为:
- (10 points) 基于第二小问和第三小问的结果, 从概率角度讨论为什么 \(L_{1}\) 范数可以使模型参数变得稀疏
解:
在 MAP 框架下,正则项本质上是 负对数先验。不同的先验分布在对数空间中呈现不同形状的惩罚:
| 先验分布 | \(\log p(\pmb{w})\) 的形状 | 对应的正则项 | 产生的约束几何 |
|---|---|---|---|
| 高斯 \(\mathcal N(\mathbf 0,\lambda\pmb I)\) | \(-\frac{1}{2\lambda}|\pmb{w}|_{2}^{2}\)(二次) | \(L_{2}\) 二次惩罚 | 欧氏球 (圆形) |
| 拉普拉斯 \(\prod_{j}\operatorname{Lap}(w_{j}\mid0,\lambda)\) | \(-\frac{1}{\lambda}|\pmb{w}|_{1}\)(线性) | \(L_{1}\) 线性惩罚 | 菱形 |
1 先验本身的特性
- 高斯先验在零点处是 平滑且可微 的,惩罚随 \(|w|\) 的增大而以 二次速度 增长。它对权重的作用是“均匀收缩”,即使权重很小也会被拉向零,但 极少恰好等于零,因为其概率密度在 \(w=0\) 并不比邻近点更大
- 拉普拉斯先验在零点处有一个 尖峰(不可微),并且尾部比高斯更重(指数衰减 vs. 二次指数衰减)。在对数空间中,惩罚是 线性 的 \(-|w|/\lambda\)。线性惩罚意味着当 \(|w|\) 很小时,先验对数密度的下降速度 比二次慢,从而 在零点附近产生更强的“拉力”,驱使那些对似然贡献不大的系数 恰好取零
2 凸优化几何视角
- 似然的等高线:对最小二乘而言,\(\|\pmb{X}\pmb{w}-\pmb{y}\|_{2}^{2}\) 的等高线是椭圆形(二次函数),中心在普通最小二乘解 \(\pmb{w}_{\text{OLS}}\) - 约束区域:
- \(L_{2}\) 约束 \(\|\pmb{w}\|_{2}^{2}\le C\) 是球形。球与椭圆的交点通常位于圆弧上,极少落在坐标轴上,故得到的 \(\pmb{w}\) 通常 全部非零
- \(L_{1}\) 约束 \(\|\pmb{w}\|_{1}\le C\) 是菱形。菱形的顶点正好位于各个坐标轴上。当椭圆与菱形相交时,最优解极容易落在顶点,即某些坐标恰好为零,从而产生稀疏解
3 子梯度条件
对 Lasso 目标函数
求次梯度得
其中 \(\operatorname{sign}(w_{j})\) 在 \(w_{j}=0\) 时取任意值于 \([-1,1]\)。于是 \(w_{j}=0\) 的充要条件是
即当第 \(j\) 个特征对残差的贡献不够大时,正则项直接把该系数 “截断”到零。这正是拉普拉斯先验在 MAP 框架下的数学体现
4 与层次化高斯先验的联系
拉普拉斯先验可以写成尺度混合高斯:
其中 \(\operatorname{Exp}\) 为指数分布。对每个 \(w_{j}\),先验在 \(\tau_{j}\) 上积分后即得到 \(\operatorname{Lap}(w_{j}\mid0,\lambda)\)
这种层次化解释说明:拉普拉斯先验等价于 每个系数拥有自己的方差,而这些方差又服从指数分布——大部分方差被压得很小(导致 \(w_{j}\approx0\)),少数方差可以很大(保留显著特征)。这正是稀疏性的贝叶斯根源
三. (20 points) 朴素贝叶斯分类器
给定一个数据集, 其中包含两个特征 \(x_{1} \in \{-1,0,1\}\) 和 \(x_{2} \in \{B,M,S\}\) , 样本标记 \(y \in \{0,1\}\) . 数据集中一共包含 15 个样例, 如表 1 所示.
| ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| x1 | -1 | -1 | -1 | -1 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| x2 | B | M | M | B | B | B | M | M | S | S | S | M | M | S | S |
| y | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
Table 1: 包含 15 个样本的数据集
- (5 points) 通过查表直接给出样例 \(\pmb{x} = \{0, S\}\) 的标记;
- (5 points) 使用所给的数据集训练一个朴素贝叶斯分类器, 并使用分类器预测样例 \(\boldsymbol{x} = \{0, S\}\) 的标记, 要求写出详细的过程;
- (5 points) 使用“拉普拉斯修正”,再学习一个朴素贝叶斯分类器,并使用分类器预测样例 \(\boldsymbol{x} = \{0, S\}\) 的标记,要求写出详细计算过程;
- (5 points) 请说明如果特征中存在连续值, 朴素贝叶斯分类器应如何处理; 如果连续特征为双峰分布, 是否会存在问题, 为什么?
解:
1.
通过查表,样例 \(\pmb{x} = \{0, S\}\) 对应 ID 9、10、11 的样本,其标记均为 \(y = 1\)。因此,该样例的标记为 1
2.
使用数据集训练朴素贝叶斯分类器。首先计算先验概率:
\(P(y=0) = 6/15 = 0.4\),\(P(y=1) = 9/15 = 0.6\)
条件概率:
对于 \(y=0\):\(P(x_1=0|y=0) = 2/6 = 1/3\),\(P(x_2=S|y=0) = 1/6\)
对于 \(y=1\):\(P(x_1=0|y=1) = 4/9\),\(P(x_2=S|y=1) = 4/9\)
对于样例 \(\pmb{x} = \{0, S\}\):
\(P(y=0|\pmb{x}) \propto 6/15 \times 2/6 \times 1/6 = 1/45 \approx 0.0222\)
\(P(y=1|\pmb{x}) \propto 9/15 \times 4/9 \times 4/9 = 16/135 \approx 0.1185\)
由于 \(16/135 > 1/45\),预测标记为 1
3.
拉普拉斯修正公式:
其中 \(N\) 为类别数 (此处为 2),\(N_i\) 为第 \(i\) 个特征可能的取值数
- \(x_1 \in \{-1, 0, 1\}\),故 \(N_1 = 3\)* \(x_2 \in \{B, M, S\}\),故 \(N_2 = 3\)
步骤 1:计算修正后的先验概率
步骤 2:计算修正后的条件概率
-
对于 \(y=0\) 的类别:
\[P(x_1=0 | y=0) = \frac{2 + 1}{6 + 3} = \frac{3}{9} = \frac{1}{3} \]\[P(x_2=S | y=0) = \frac{1 + 1}{6 + 3} = \frac{2}{9} \] -
对于 \(y=1\) 的类别:
\[P(x_1=0 | y=1) = \frac{4 + 1}{9 + 3} = \frac{5}{12} \]\[P(x_2=S | y=1) = \frac{4 + 1}{9 + 3} = \frac{5}{12} \]
步骤 3:计算后验概率并比较
-
计算 \(y=0\) 的得分:
\[Score_0 = \frac{7}{17} \times \frac{1}{3} \times \frac{2}{9} = \frac{14}{459} \approx 0.0305 \] -
计算 \(y=1\) 的得分:
\[Score_1 = \frac{10}{17} \times \frac{5}{12} \times \frac{5}{12} = \frac{250}{2448} \approx 0.1021 \]
结论:
因为 \(0.1021 > 0.0305\),所以分类器预测样例 \(\boldsymbol{x} = \{0, S\}\) 的标记为 1
4.
连续值的处理:
如果特征是连续值,朴素贝叶斯通常假定该特征服从高斯分布(正态分布)
处理步骤如下:
- 计算训练集中每个类别 \(c\) 下,该特征 \(i\) 的均值 \(\mu_{c,i}\) 和方差 \(\sigma_{c,i}^2\) 2. 在预测时,代入高斯概率密度函数计算条件概率:
(注:另一种方法是将连续值离散化/分桶,但在朴素贝叶斯中高斯假设最为常见)
双峰分布是否存在问题:
会存在问题
原因:
高斯分布是单峰的,它假设数据围绕一个中心均值对称分布
如果实际特征数据呈现双峰分布,意味着数据有两个高密度区域。如果我们强制使用高斯分布去拟合:
- 计算出的均值通常会落在两个峰之间的低密度区域(谷底)
- 计算出的方差会很大,以试图覆盖两个峰
- 这将导致模型在预测时,给予两个实际高密度区域较低的概率密度,而给予中间低密度区域(均值附近)较高的概率密度,从而严重扭曲真实的概率分布,导致分类性能下降
(解决双峰问题通常需要使用核密度估计(KDE)或先对数据进行离散化处理)
四. \((25 + 10\) points)神经特征增强的SVM
以 Kernel SVM 为首的传统核方法通常依赖固定的核函数, 无法自适应地学习任务相关的特征表示; 而神经网络虽然缺乏理论透明度, 但具备强大的特征学习能力. 本次作业将探索如何结合两者的优势.
请结合提供的6个表格数据集和demo.py代码框架,完成下面的编程题目:
- (5 points) 请基于 sklearn.svm 实现一个 Kernel SVM.
- (10 points) 请基于 pytorch 实现一个包含至少一个隐藏层的 MLP, 需要使用验证集做模型选择。在提供的数据集上测试并比较两种模型的性能
- (10 points) 验证神经网络的“特征学习”能力是否可以转移给 SVM 使用。神经网络的第一层通常被认为是在学习输入数据的低级特征,请尝试使用上一小题中训练好的 MLP 的第一层作为 Kernel SVM 的特征提取层。设输入为 \(\mathbf{x}\) ,第一层权重为 \(W_{1}\) ,偏置为 \(b_{1}\) ,激活函数为 \(\sigma(\cdot)\) ,则 MLP 第一层变换后的数据为 \(z = \sigma(W_{1} \mathbf{x} + b_{1})\) 。对训练集和测试集的所有样本进行此变换,得到新的数据集 \((Z_{\text{train}}, y_{\text{train}})\) 和 \((Z_{\text{test}}, y_{\text{test}})\) ,使用变换后的特征 \(Z_{\text{train}}\) 训练一个新的 Kernel SVM,并比较这种方法与前两问中两 baseline 方法的性能
- (10 points bonus) 这篇论文提出了神经特征假设 (Neural Feature Ansatz, NFA), 并基于此设计了一种递归特征机器 (Recursive Feature Machine, RFM) 算法. RFM 仅有 Kernel SVM 的非线性能力, 但达到了表格学习中的第一梯队性能. 请就以下问题谈谈你的看法:
- 请解释什么是NFA,以及论文认为神经网络的每一层实际上是在计算什么统计量?
- 现在的RFM依赖交替优化AGOP和SVM,你有什么将其与迭代优化的神经网络结合的思路?
请将运行结果整理在答题框内,并以Python文件的形式提交代码
解:
结果粘贴如下:
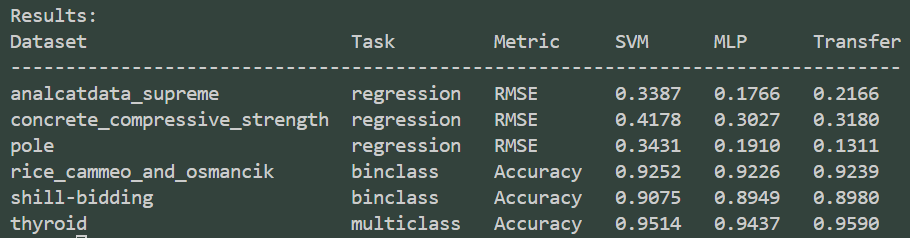
4.
1).
Neural Feature Ansatz (NFA) 是由 Radhakrishnan 等人提出的一种假设,旨在解释神经网络如何学习特征。NFA 指出,神经网络的每一层权重矩阵(具体来说是 Neural Feature Matrices, NFMs)在训练后会趋向于与该层输入的 平均梯度外积成正比
数学上,对于神经网络的第 \(l\) 层,如果其权重为 \(W_l\),NFA 认为:
其中 \(h_{l-1}\) 是第 \(l\) 层的输入(即上一层的输出),\(f(x)\) 是模型的输出
根据 NFA,神经网络的每一层实际上是在计算(或学习)AGOP (Average Gradient Outer Product)
AGOP 是一个统计量,它捕获了模型输出对输入的敏感度方向
- AGOP 的特征向量对应于模型预测最依赖的输入方向(即“任务相关特征”)
- AGOP 的特征值表示这些方向的重要性
因此,神经网络的每一层都在通过调整权重,使其特征提取能力(由 \(W^T W\) 刻画)与模型在该层输入上的敏感度结构(由 AGOP 刻画)相对齐。这意味着网络在不断地“放大”那些对预测结果影响最大的方向上的信号
2).
RFM (Recursive Feature Machine) 通过交替进行“训练 Kernel Machine”和“计算 AGOP 并更新 Kernel Metric”来工作。这是一种显式的、迭代的特征学习过程
将 RFM 的思想与神经网络的迭代优化(通常指基于梯度的优化,如 SGD)结合,可以有以下几种思路:
-
基于 AGOP 的层初始化或重置 :
在神经网络训练的某些阶段(例如每隔若干个 epoch),可以计算当前网络各层的 AGOP,并显式地调整该层的权重矩阵,使其奇异向量与 AGOP 的特征向量对齐。这可以看作是一种“纠正”或“加速”特征学习的手段,帮助网络跳出局部极小值或更快地找到相关特征。 -
显式的特征度量更新步骤:
类似于 RFM 更新 Kernel 的马氏距离矩阵 \(M\),我们可以在神经网络训练中引入一个显式的“特征度量”参数 \(M_l\) 插入在层与层之间(例如 \(z = \sigma(W_l M_l x + b)\))- Step 1 (Weight Update): 固定 \(M_l\),使用反向传播更新 \(W_l, b_l\)
- Step 2 (Metric Update): 固定 \(W_l, b_l\),计算该层的 AGOP,并直接更新 \(M_l \leftarrow \text{AGOP}\) (或其平滑版本)
这种交替优化策略可能比单纯的端到端反向传播更有效地捕获特征,特别是对于深层网络
-
Deep RFM / 逐层贪婪训练:
RFM 本质上是在输入空间学习特征。我们可以将其扩展为多层结构:- 使用 RFM 学习第一层特征变换(非线性映射)
- 固定第一层,将变换后的数据作为输入,再次使用 RFM 学习第二层特征变换
- 如此堆叠,构建一个“深度 RFM”。这类似于逐层预训练,但使用 RFM 机制来替代传统的 Autoencoder 或 RBM
-
正则化项:
可以将 NFA 作为一个正则化项加入到损失函数中:\[\mathcal{L}_{total} = \mathcal{L}_{pred} + \lambda \sum_l \| W_l^T W_l - \text{AGOP}_l \|_F^2 \]强制网络的权重结构与 AGOP 保持一致,这可能提高模型的泛化能力和可解释性




 浙公网安备 33010602011771号
浙公网安备 33010602011771号