实验二
2.1
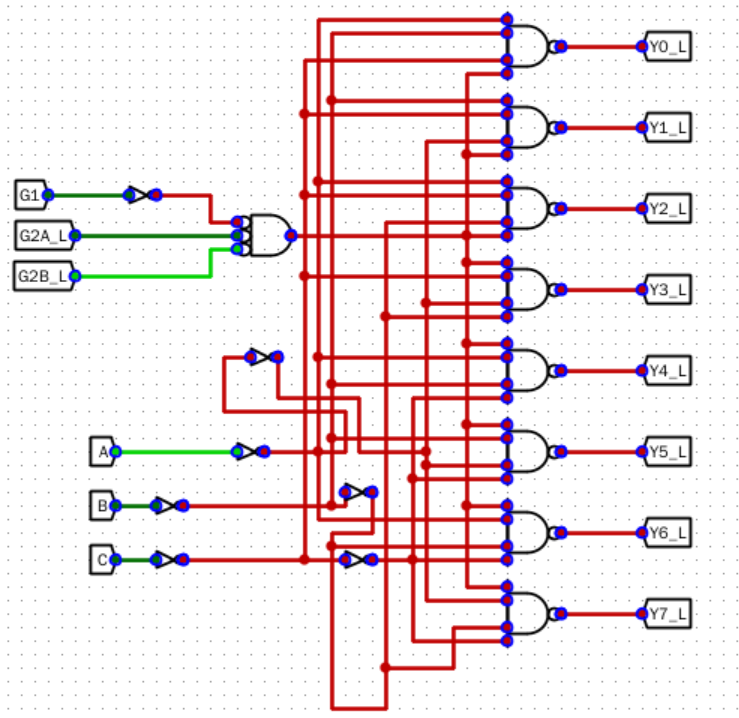
- 设计一个由反相逻辑门电路构成的 3-8 译码器,并对电路进行仿真测试,以验证电路的功能。
整体方案设计
输入输出引脚
- \(G1、G2A_L、G2B_L\):三个控制位
- \(ABC\):三位二进制输出
- \(Yi_L\)(\(i=0,1,2,...,7\)):8位译码后的二进制输出
原理图
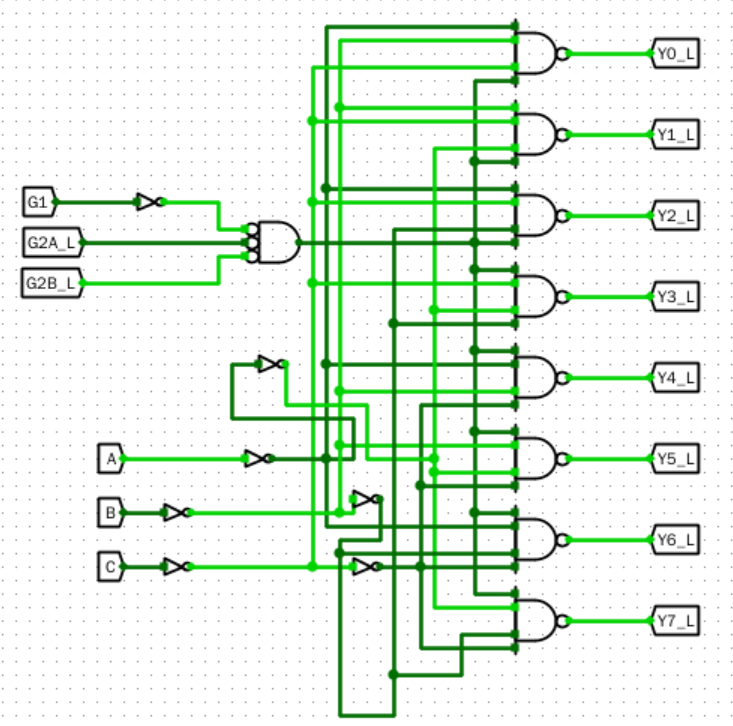
电路图

仿真测试
- 初始状态
![image]()
- 第一步
![image]()
- 第二步
![image]()
- 第三步
![image]()
- 第四步
![image]()
- 第五步
![image]()
可以看到结果符合预期

错误现象及分析
没有遇到错误
2.2
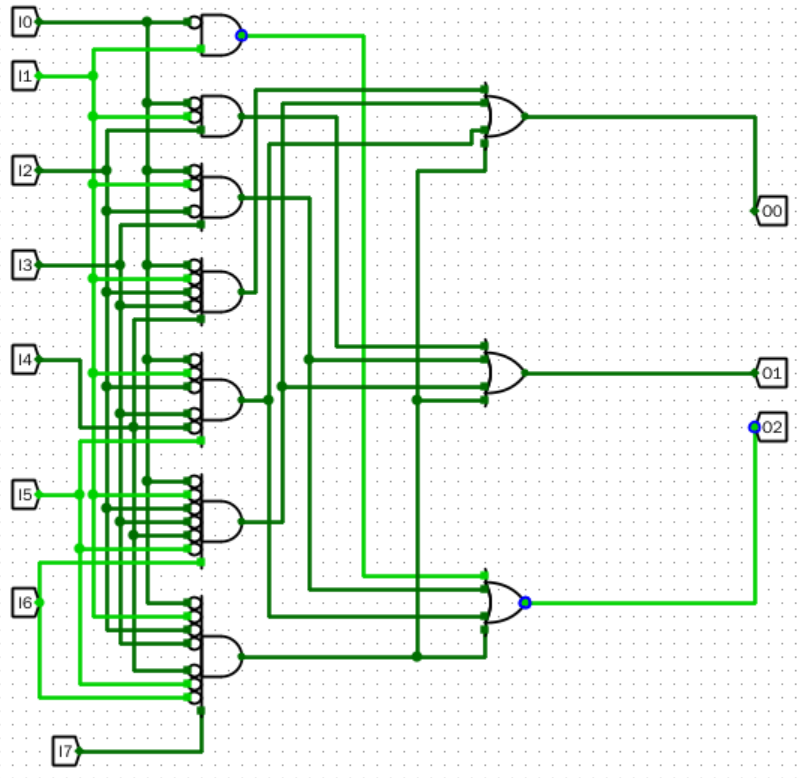
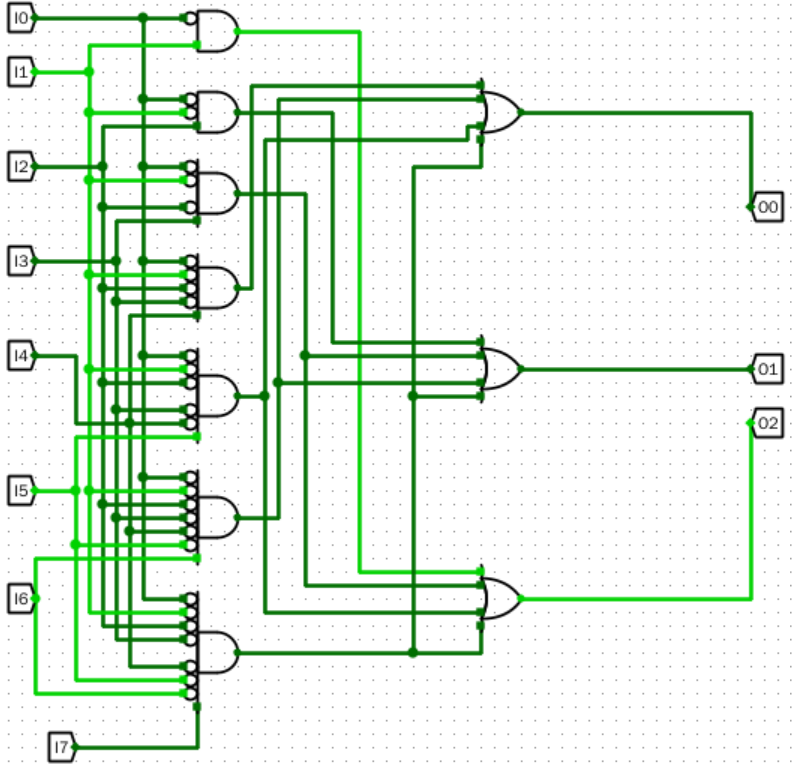
- 设计一个由逻辑门电路构成的 8-3 优先级编码器,并将编码器输出连接到一个十六进制数码管,通过数码管的输出显示来验证和测试电路。
整体方案设计
输入输出引脚
- \(Ii\)(\(i=0,1,2,...,7\)):8位输入
- \(O_0,O_1,O_2\):3为编码结果输出
原理图

电路图
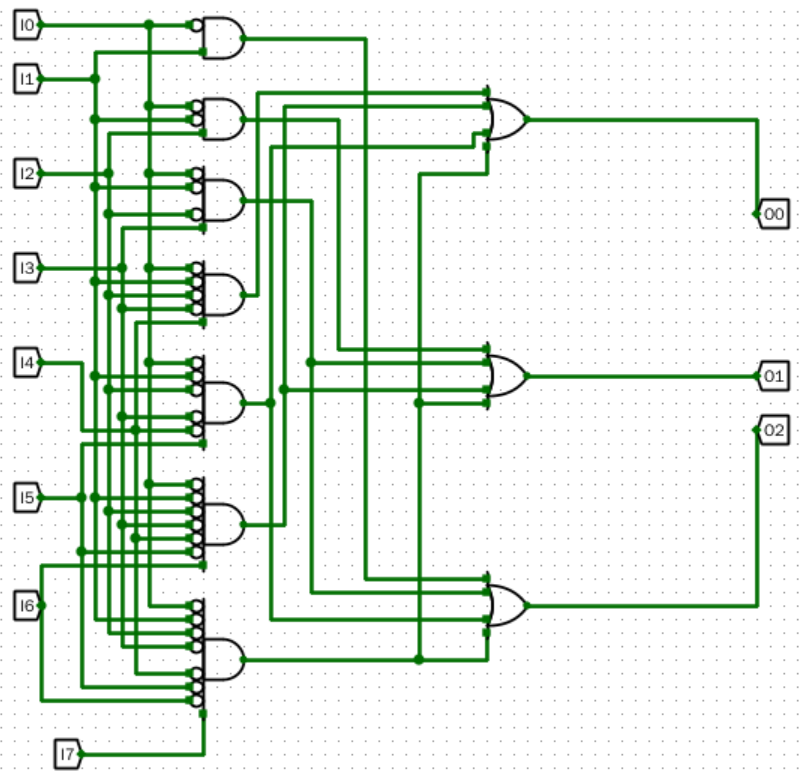
仿真测试
- 初始状态
![image]()
- 第一步
![image]()
- 第二步
![image]()
- 第三步
![image]()
- 第四步
![image]()
- 第五步
![image]()
可以看到上述电路没有问题

错误现象及分析
没有遇到错误
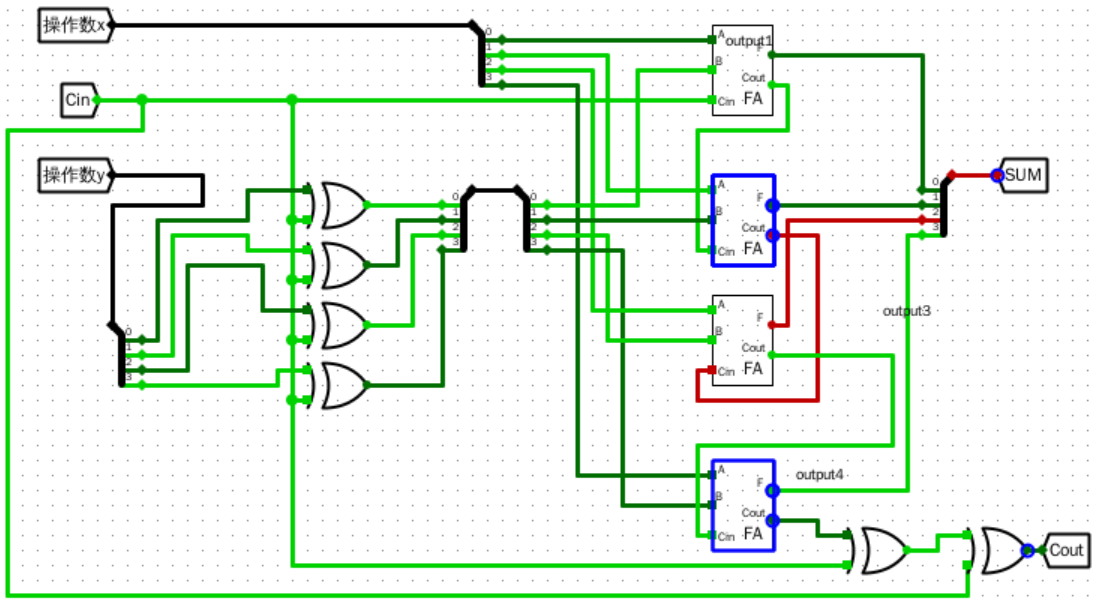
2.3
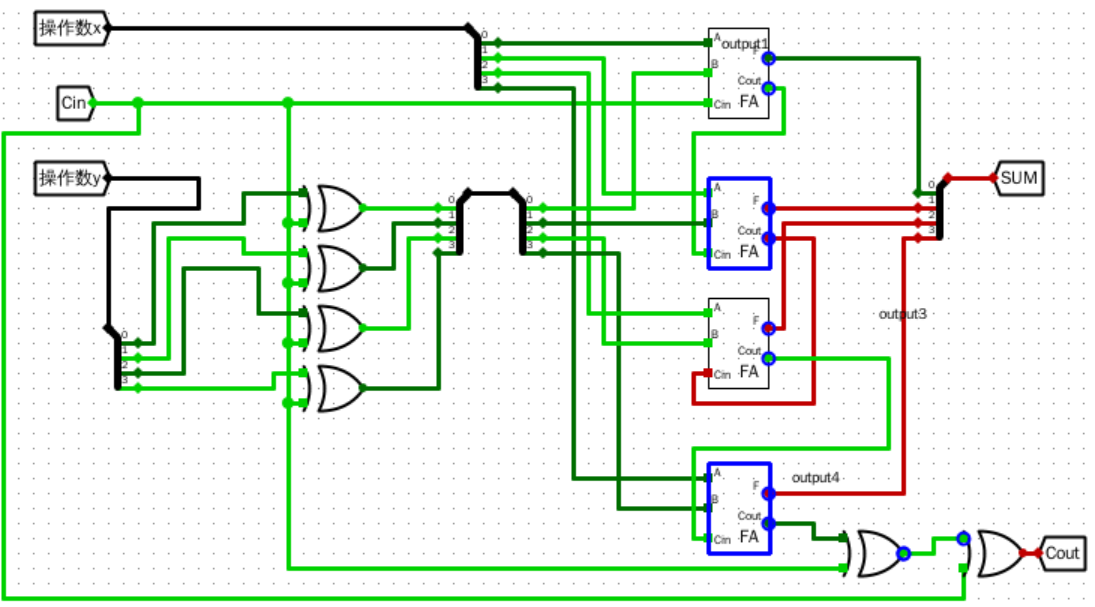
- 设计一个支持4位数加减法的器件
整体方案设计
输入输出引脚
- \(X\):被加(减)数
- \(Y\):加(减)数
- Cin:模式选择
- Cout:进位
原理图

电路图

仿真测试
- 初始状态
![image]()
- 第一步
![image]()
- 第二步
![image]()
- 第三步
![image]()
- 第四步
![image]()
- 第五步
![image]()
- 第六步
![image]()
- 第七步
![image]()
- 第八步
![image]()
- 第九步
![image]()
- 第十步
![image]()
- 第十一步
![image]()
- 第十二步
![image]()
- 第十三步
![image]()
- 第十四步
![image]()
- 第十五步
![image]()
可以看到电路符合状态
错误现象及分析
没有遇到错误
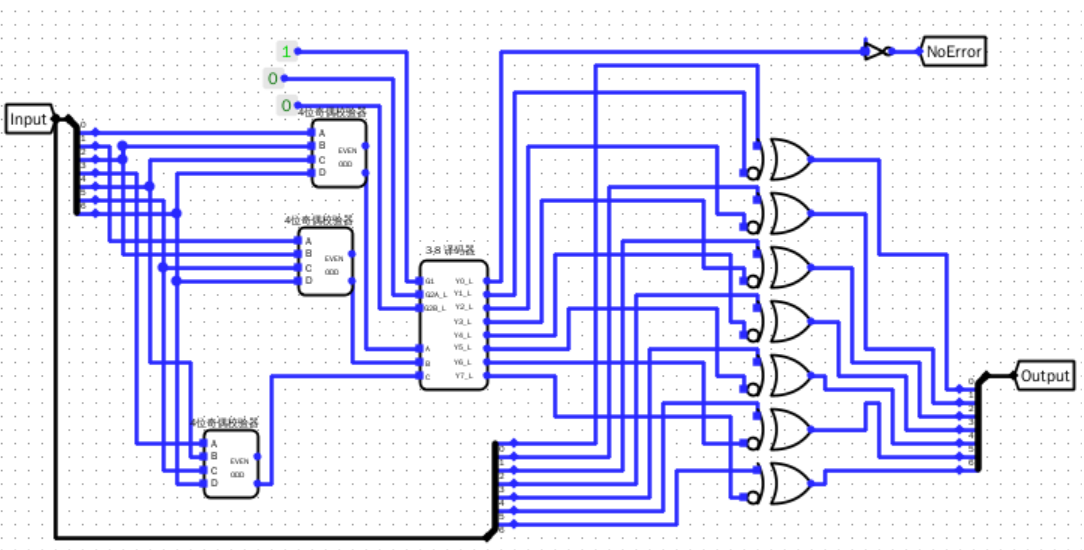
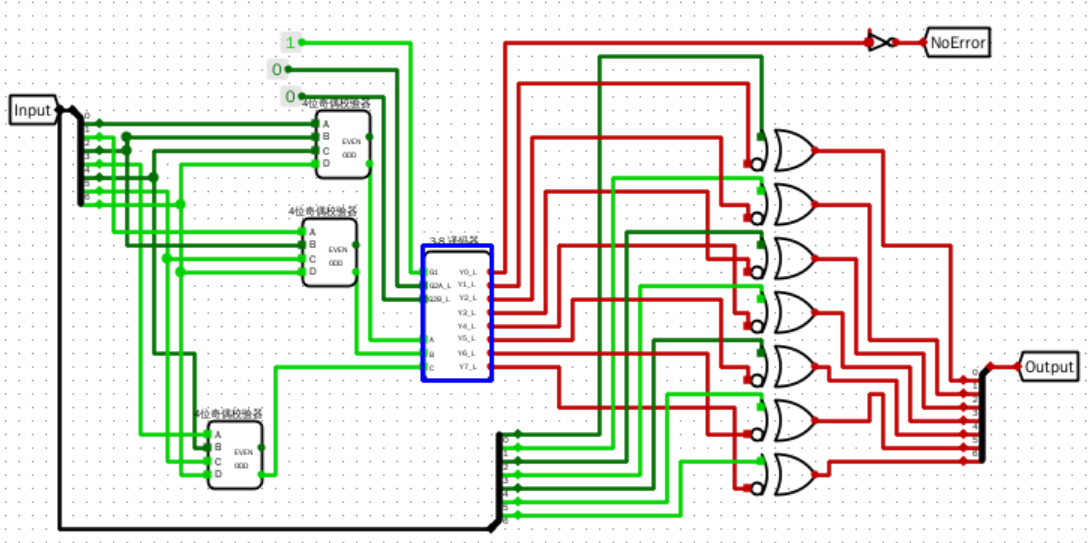
2.4
- 设计一个支持7位汉明码校验及自动纠错的元器件
整体方案设计
输入输出引脚
- Input:输入的7位
- Output:校验结果
- NoError:是否出错的判定
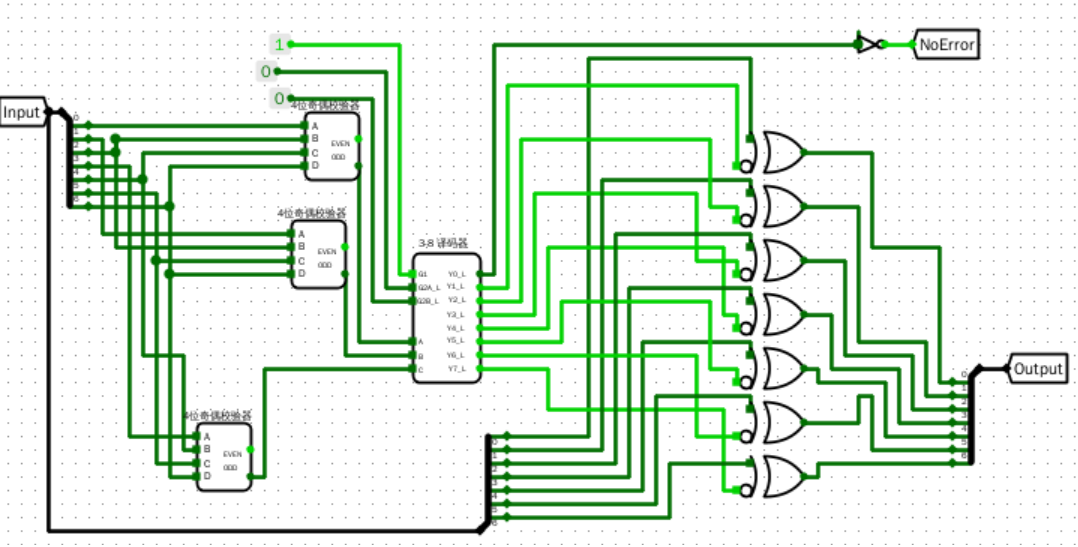
原理图

电路图
主电路
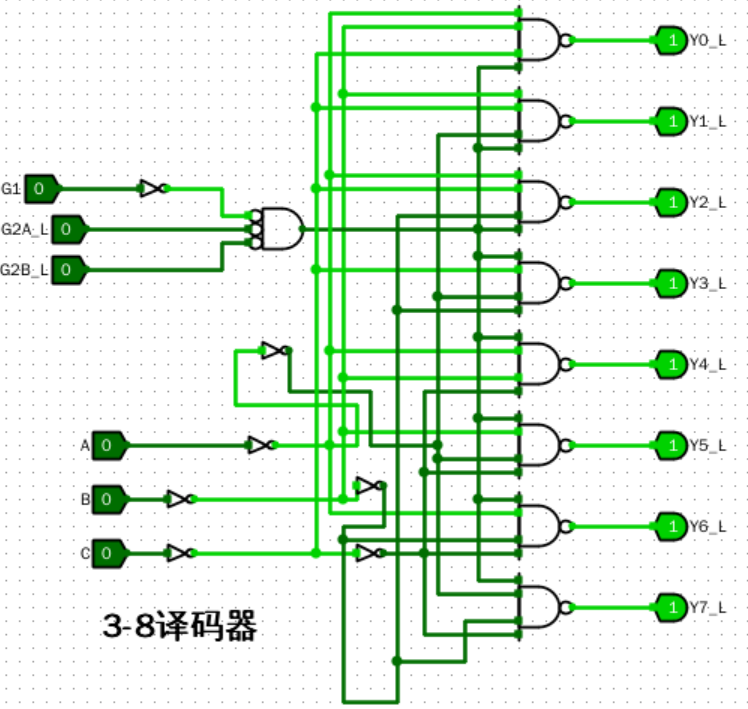
3-8 译码器
4位奇偶校验器

仿真测试
- 初始状态
![image]()
- 第一步
![image]()
- 第二步
![image]()
- 第三步
![image]()
- 第四步
![image]()
- 第五步
![image]()
- 第六步
![image]()
- 第七步
![image]()
- 第八步
![image]()
- 第九步
![image]()
- 第十步
![image]()
- 第十一步
![image]()
- 第十二步
![image]()
- 第十三步
![image]()
可以看到没有问题
错误现象及分析
没有遇到错误
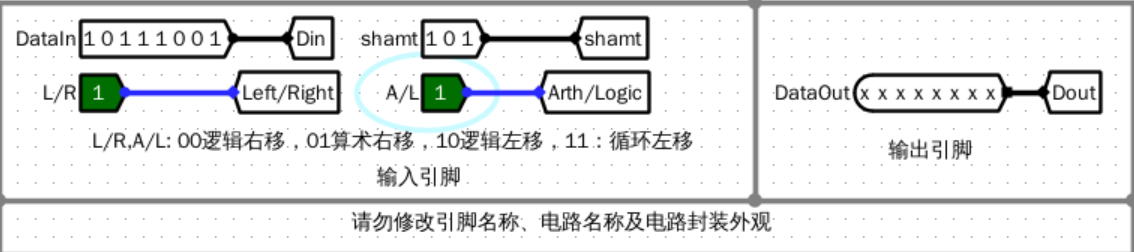
2.5
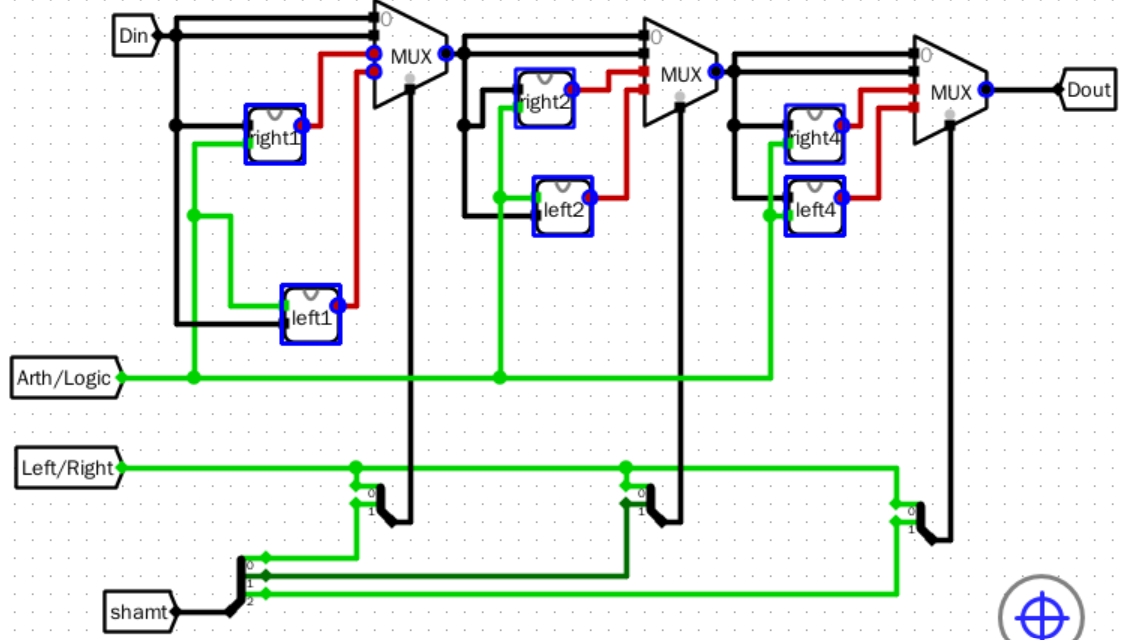
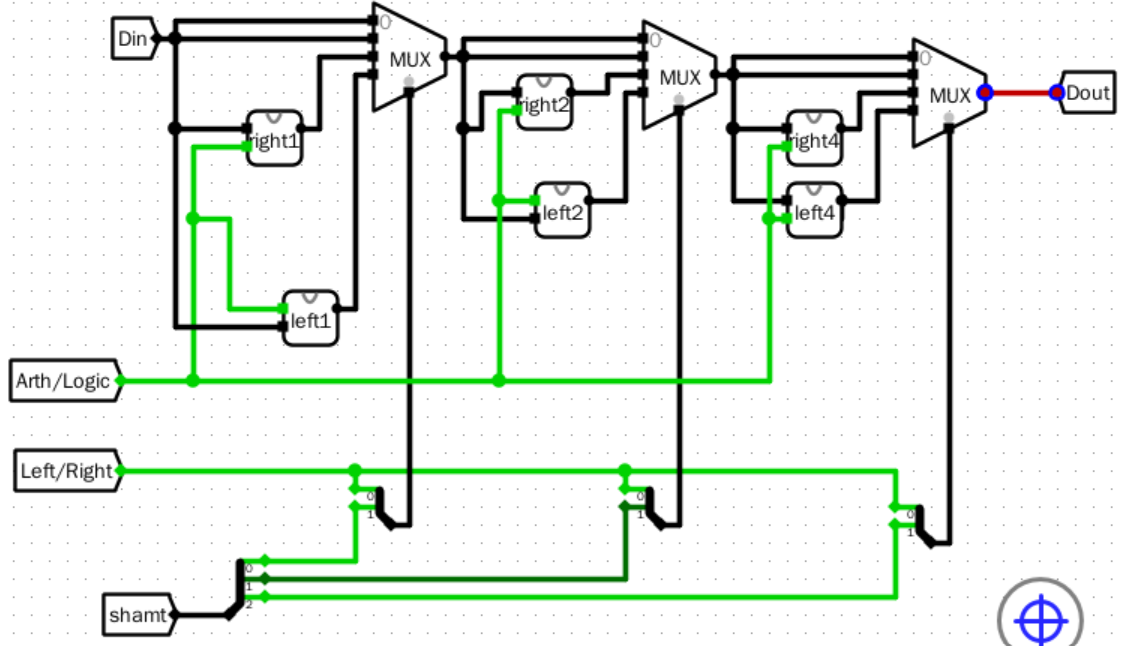
- 设计一个支持8位数左右移的元器件
整体方案设计
输入输出引脚
- DataIn:Din输入的8位数字
- Dout:移位后的结果
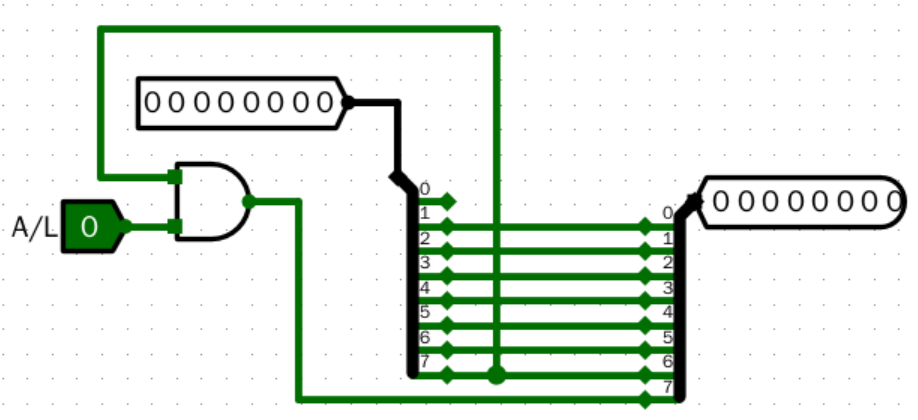
- L/R:移动方向设置
- A/L:移动方式选择
- shamt:移动位数
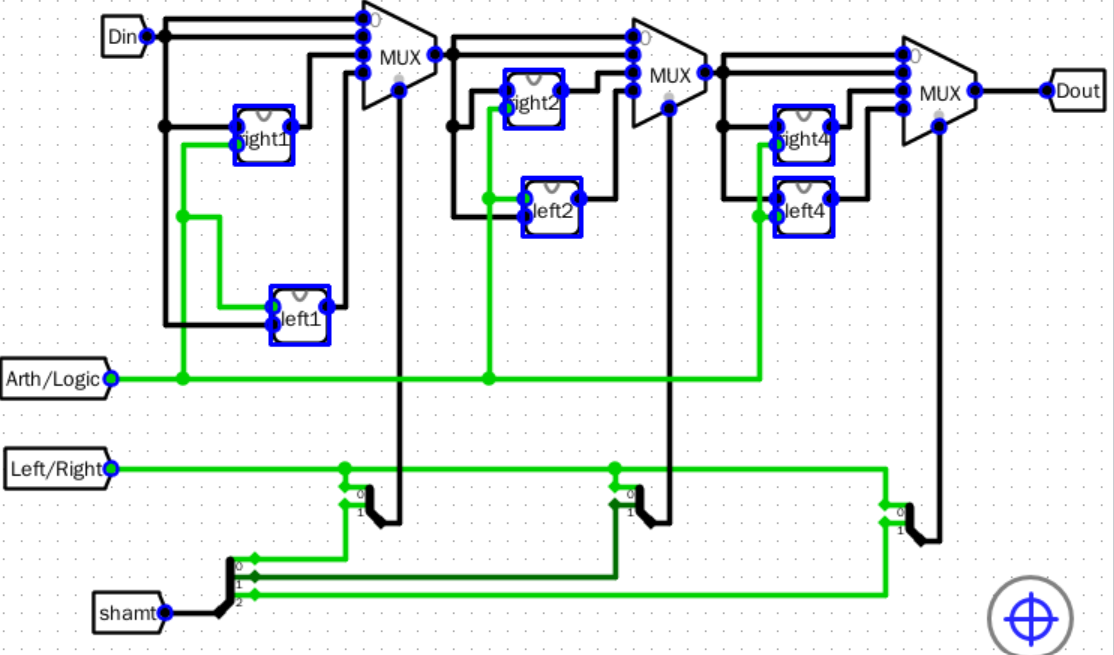
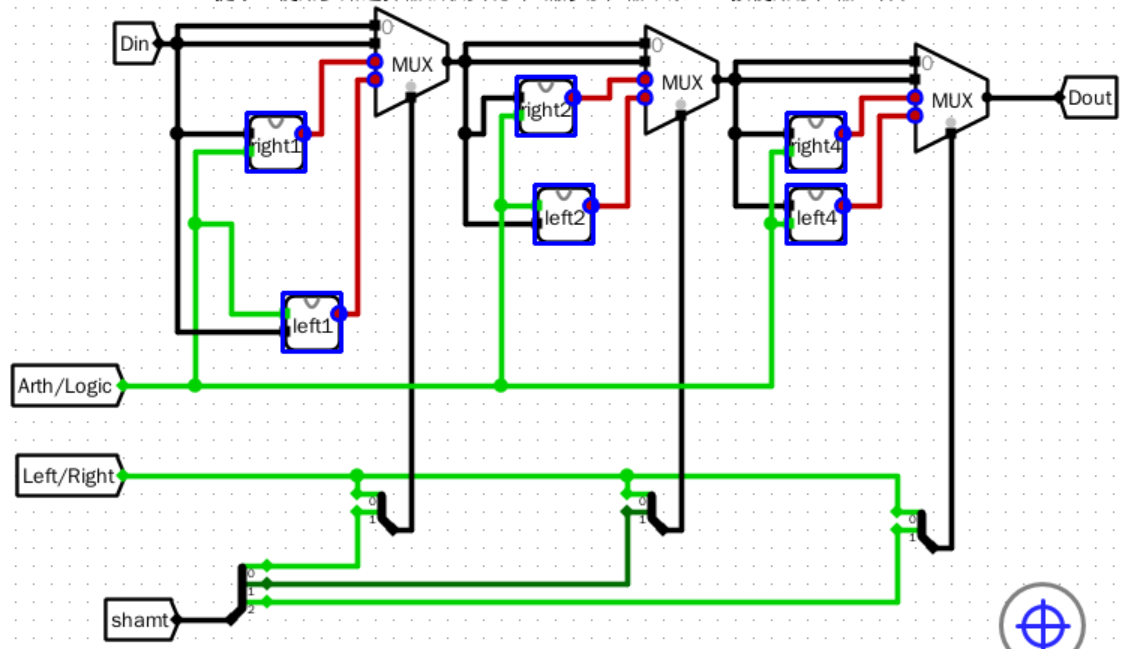
原理图

电路图
左移一位
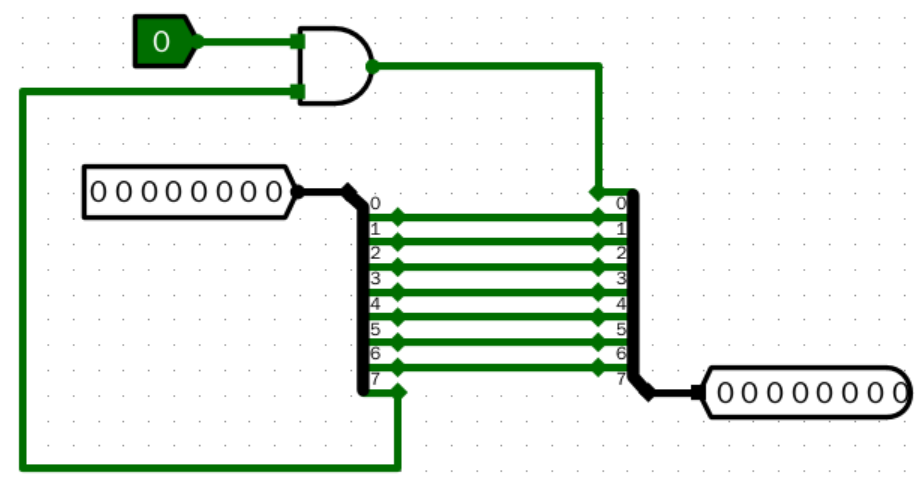
左移两位

左移四位
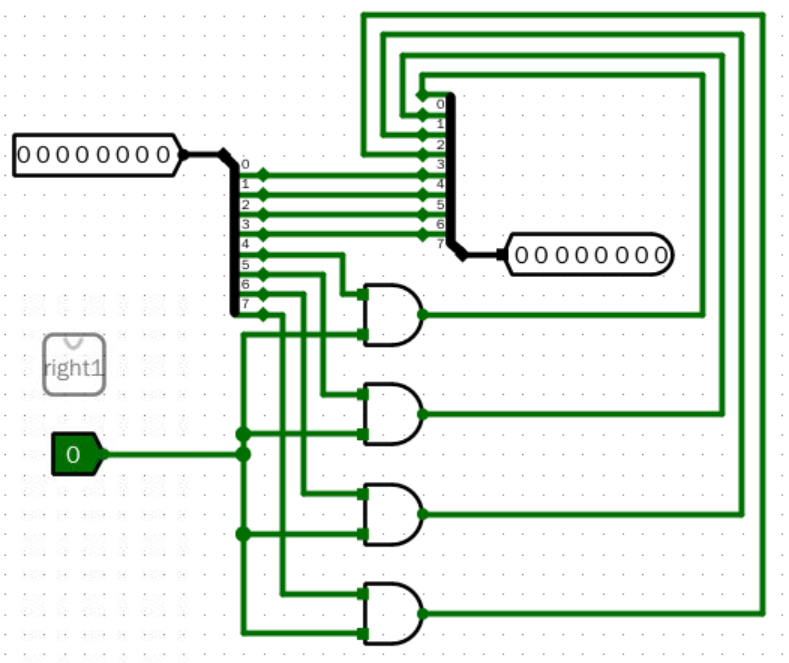
右移一位
右移两位

右移四位

主电路

仿真测试
- 初始状态
![image]()
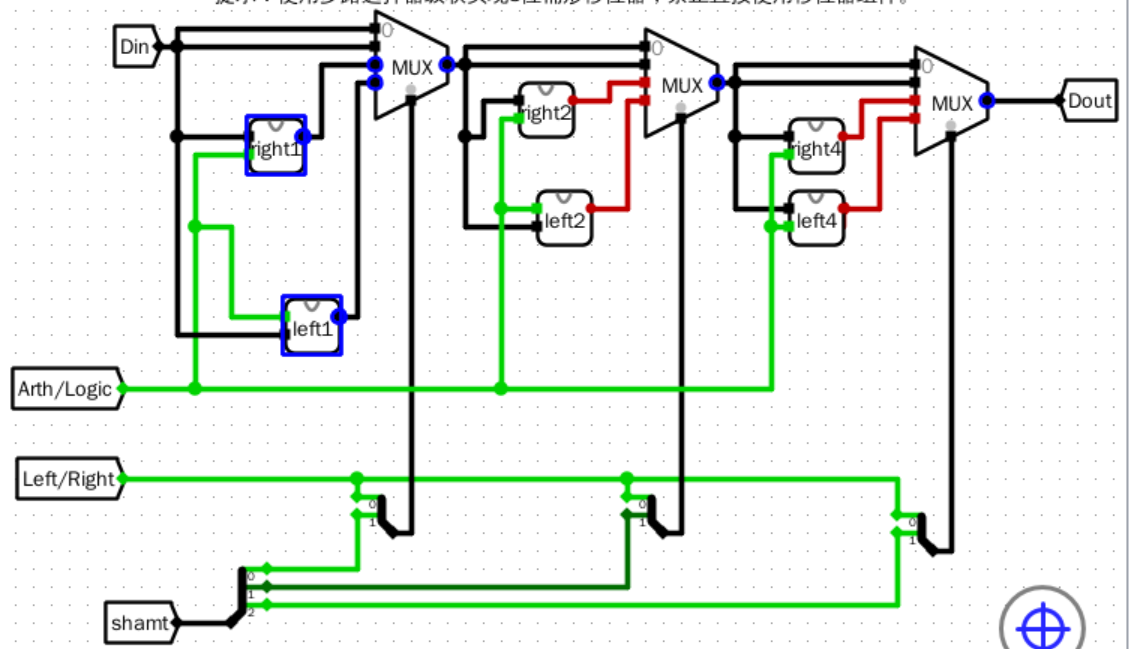
- 第一步
![image]()
- 第二步
![image]()
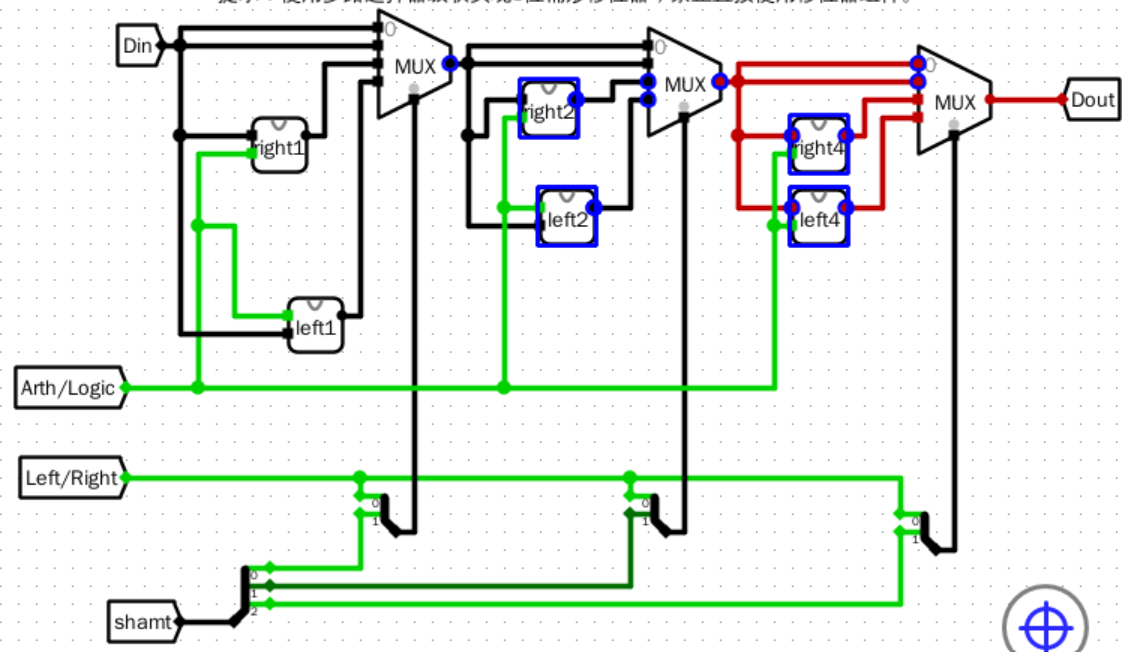
- 第三步
![image]()
- 第四步
![image]()
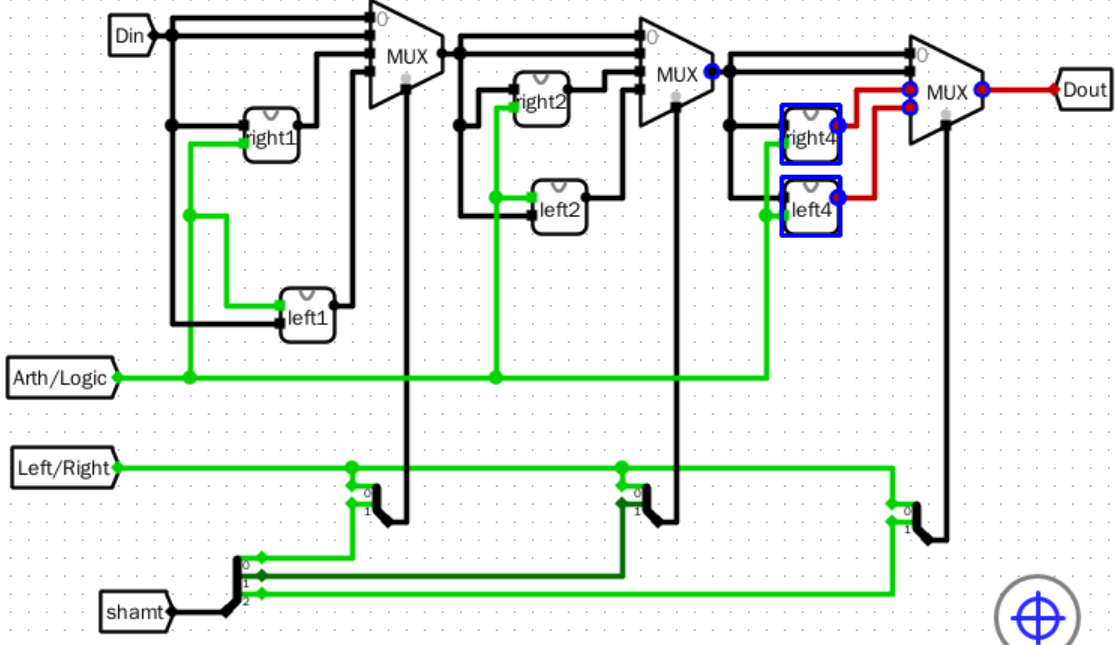
- 第五步
![image]()
- 第六步
![image]()
- 第七步
![image]()
- 第八步
![image]()
- 第九步
![image]()
- 第十步
![image]()
- 第十一步
![image]()
- 第十二步
![image]()
- 第十三步
![image]()
- 第十四步
![image]()
- 第十五步
![image]()
- 第十六步
![image]()
- 第十七步
![image]()
可以看到没有问题
错误现象及分析
没有遇到错误
思考题
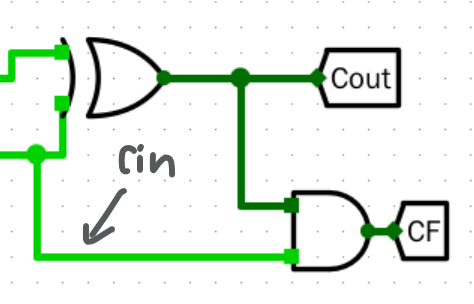
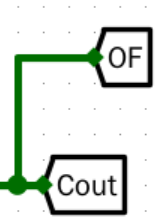
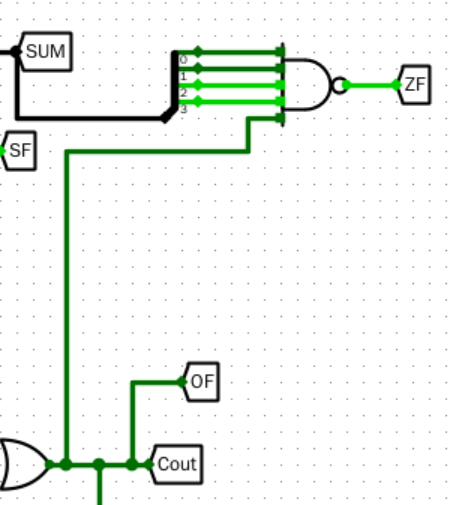
修改实验中的加法器电路,生成进位标志 CF、溢出标志 OF、符号标志 SF 和结果为零标志位 ZF。
- CF
![image]()
- OF
![image]()
- SF
![image]()
- ZF
![image]()
通过带标志位加法器输出(X>Y)等于和(X<Y)小于的信号
参考CSAPP可以得出下面的结论
无符号整数
- ZF=1:X和Y相等
- ZF=0 且 CF=1:X小于Y
- 如果 ZF=0 且 CF=0:X大于Y
有符号整数
- ZF=1:X和Y相等
- ZF=0 且 SF=0 且 OF=0 或 SF=1 且 OF=1:X大于Y
- 如果 ZF=0 且 SF=0 且 OF=1 或 SF=1 且 OF=0:X小于Y
不使用加法器直接使用逻辑门电路实现 4 位无符号二进制数比较器,输出大于和小于二个结果
-
逐位比较的基本信号:
- 对于每一位\(i\)(从3到0):
- \(gt_i = A_i \overline{B_i}\) // \(A_i > B_i\) 时为1
- \(lt_i = \overline{A_i}B_i\) // \(A_i < B_i\) 时为1
- \(eq_i = \overline{A_i \oplus B_i}\) // \(A_i == B_i\) 时为1
- 对于每一位\(i\)(从3到0):
-
比较过程:
- \(GT (A > B)\):从最高位开始,如果某位\(A > B\)且之前所有高位相等,则\(GT=1\)。
- 表达式:\(GT = gt_3 + (eq_3 gt_2) + (eq_3 eq_2 gt_1) + (eq_3 eq_2 eq_1 gt_0)\)
- \(LT (A < B)\):类似,但检查\(A < B\)。
- 表达式:\(LT = lt_3+(eq_3 lt_2) + (eq_3 eq_2 lt_1) +(eq_3 eq_2eq_1 lt_0)\)
- \(GT (A > B)\):从最高位开始,如果某位\(A > B\)且之前所有高位相等,则\(GT=1\)。
如何使用 8 位桶形移位器扩展到 32 位桶形移位器
首先,将一个32位的操作数按字节拆解为四个8位二进制段,从最低有效字节到最高有效字节依次标记为 A、B、C、D
具体实现上,可将32位数据划分为4个独立的8位单元。每个单元均可借助现成的8位桶形移位器完成移位处理,再将这四个移位器按顺序级联构成一条移位链。其中,第一个移位器负责处理最低8位(A),第二个处理紧邻其上的8位(B),依此类推
当需要执行 4 位、2 位或 1 位的移位组合时,仅需串联一组(共4个)8位桶形移位器即可达成目标。此时,shamt信号的低三位作为该组移位器的控制输入。但为了支持跨字节移位,需对桶形移位器的输入结构做适当调整:
修改方案:在原有输入基础上增加“待移入位”字段。例如,在右移场景中,“待移入位”应作为高位补入。以处理B字节的移位器为例,其输入应包含B和C两个字节;同理,对于最高位字节D,在逻辑右移时直接高位补0(若为算术右移,则依据符号位扩展补值)。如此设计,即可完整支持0至7位范围内的32位数据移位
若移位量大于等于8位但小于16位,建议采用两组串联的8位桶形移位器(共计8个),即将整个移位过程分解为两个阶段。例如,若需右移12位,可先执行6位移位,再追加一次6位移位。而对于移位量大于等于16位的情形,则采用四组串联结构(共32个移位器),将大移位量分解为4次不超过8位的移位操作,从而完成整体功能













































 浙公网安备 33010602011771号
浙公网安备 33010602011771号