第一章习题

(1)
\((25.8125)_{10}=(11001.1101)_2=(31.64)_8=(19.D)_{16}\)
(2)
\((101101.011)_{2}=(45.375)_{10}=(55.3)_8=(2D.6)_{16}=(0100 0101.0011 0111 0101)_{8421}\)
(3)
\((0101 1001 0110.0011)_{8421}=(596.3)_{10}=(1001010100.01001100110011)_2=(254.4CCC)_{16}\)
(4)
\((4E.C)_{16}=(78.75)_{10}=(1001110.11)_{2}\)

+0.1001：符号位0，原码为01001000
-0.1001：符号位1，原码为11001000
+1.0：作为整数，符号位0，原码为00000001；作为小数的话，无法表示
-1.0：作为整数，符号位1，原码为10000001；作为小数的话，无法表示
+0.010100：符号位0，原码为00101000
-0.010100：符号位1，原码为10101000
+0：符号位0，原码为00000000
-0：符号位1，原码为10000000

+1001:补码为00001001，移码为10001001
-1001：补码为11110111，移码为01110111
+1：补码为00000001，移码为10000001
-1：补码为11111111，移码为01111111
+10100：补码为00010100，移码为10010100
-10100：补码为11101100，移码为01101100
+0/-0：补码为00000000，移码为10000000

(1)-25
(2)-128
(3)82
(4)-45

(1)(int)0xFFFF0006的十进制表示为-65530
(2)(short)0xDFFC的十进制表示为-8196
(3)(unsigned)0xFFFFFFFA的十进制表示为4294967290
(4)(char)0x2A的十进制表示为42（查询得到符号*）
(5)(float)0xC4480000的十进制表示为-800.0
(6)(double)0xC024800000000000的十进制表示为-10.25

12.(5)
移码是8位，所以e的范围是0_{255，于是E的范围是-128}127
尾数是7位，由于不能是全0，所以表示范围为\(2^{-7}\)~\(\frac{127}{128}\)
于是可以得出表示范围为\(-\frac{127}{128}\times 2^{127}\)到\(-2^{-135}\)，\(2^{-135}\)到\(\frac{127}{128}\times 2^{127}\)以及0

32位补码表示为0000 0000 0000 0000 1000 0000 0000 0010（十六进制表示为0x00008002），单精度浮点格式为0100 0101 1000 0000 0001 0000 0000 0000（十六进制表示为0x45801000），可以知道相同的序列为000000000010，这是因为补码转换为浮点数的时候，需要先转换成二进制下的科学计数法，省去了小数点左边的1之后，剩下的位数保持不变放到浮点数的尾数里再进行补全，所以是相同的

x的十六进制表示为BE000000，y的十六进制表示为40F00000，i的十六进制表示为0064
x的大端：

x的小端：

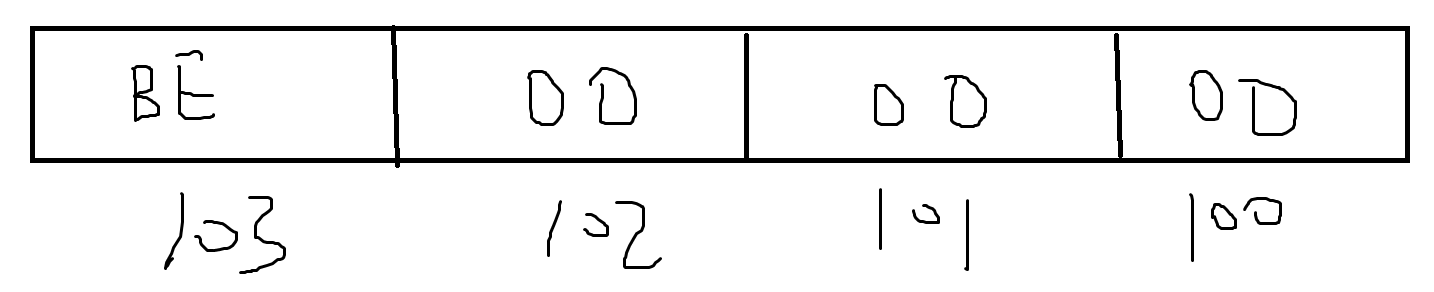
y的大端：

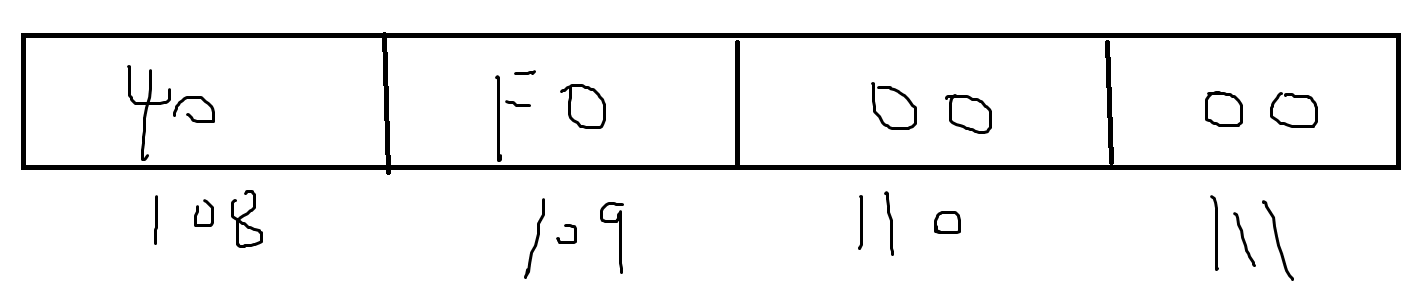
y的小端：

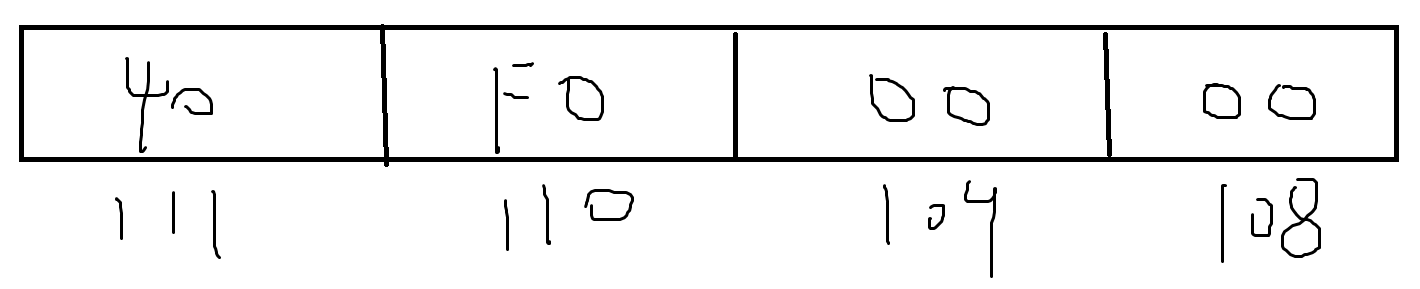
i的大端：

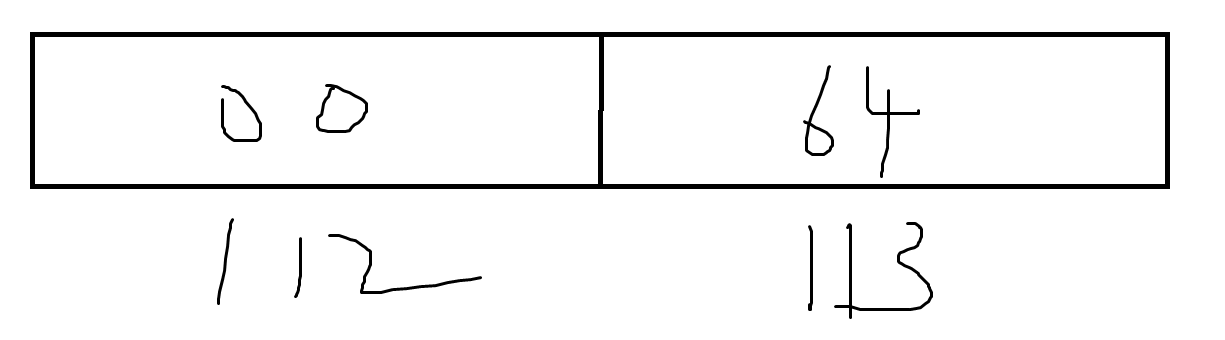
i的小端：