第七次作业

第七章：
R7
802.11是无线传播，很容易出现损坏，所以需要确认；而有线传播则不用，可以由上层的TCP去确认
P5
a.不会崩溃，因为每个AP都有自己的SSID和MAC地址，当站点发送帧的时候，AP可以通过MAC地址来判断是不是发送给自己的，只不过两个AP会共享带宽；两个站点同时传输的时候，会出现冲突
b.此时不会发生冲突
P6
基于公平性考虑。因为DIFS远小于随机回退值，所以如果站点A直接回到步骤一，那么其他站点（因为站点A在发送）会由于随机回退值继续不发送帧，然后A又可以发送下一帧。这样就不公平了，因为A发送完了应该让其他站点先发送
P7
与郑老师交流过了，很多数据都没有给，但是考试的时候会给的
RTS/CTS的长度是32字节，数据帧的长度是12384比特，所以总的时间为
DIFS + RTS + SIFS + CTS + SIFS + FRAME + SIFS + ACK=DIFS + 3SIFS+\(3\times\frac{32\times8}{11\times10^6}+\frac{12384}{11\times10^6}\)usec=DIFS + 3SIFS + 1194.82 usec
P8
a.一个报文/两个时隙。让其他的都不发，C->B->A
b.两个报文/一个时隙。D和A同时开始发送，不会冲突
c.一个报文/一个时隙。C先发，A后发
d.
对a.来说，是一个报文/时隙（假设两两之间连边）
对b.来说，仍然是两个报文/一个时隙
对c.来说，变成了两个报文/一个时隙
e.
对a.来说，一个报文/四个时隙
对b.来说，两个报文/三个时隙：AD同时发，B先发ACK，C后发ACK
对c.来说，两个报文/三个时隙：C先发，D收到后发ACK并且此时A也开始发，然后B发ACK
第八章：
R5
一共有可能有\(2^8\)种块，所以一共可能有\(2^8!\)个映射/密匙
R6
总共需要\(\frac{n(n-1)}{2}\)个密匙；若用公钥密匙系统，需要\(2n\)个密匙
R15
基于数字签名，因为MAC是需要双方知道一个秘钥s的，而且不同的双方的s还不同，而数字签名只需要利用Alice的私钥即可，所以开销更小
R23
客户端生成PMS后，使用Alice的公钥对其进行加密，然后将加密后的PMS发送给Trudy。由于Trudy没有Alice的私钥，她无法解密PMS，因此无法确定共享的密钥。Trudy可能会选择一个随机密钥来猜测。在握手过程的最后一步，Trudy使用她猜测的认证密钥，向Bob发送所有握手消息的MAC。当Bob接收到MAC后，MAC测试将失败，鲍勃会终止TCP连接
P3
不可以，因为现在是多码了，相同的字母的密文不一定唯一，还取决与这个字母的位置
P7
a.

• \(n=pq=33,z=(p-1)(q-1)=20\)
• 选择\(e=9,d=9\)
• 对每个字母独立加密
  • d：有\(4^9\%33=25\)
  • o：有\(15^9\%33=3\)
  • g：有\(7^9\%33=19\)
• 对每个加密了的字母解密
  • \(25^7\%33=4\)，故为d
  • \(3^7\%33=15\)，故为o
  • \(19^7\%33=7\)，故为g

b.将每个字母的序号转化成二进制然后拼接起来，得到报文为001000111100111，转化成十进制就是4583，选择\(p = 43, q = 107, n = p*q = 4601, z = (p-1)(q-1)= 4452. e = 61, d = 73\)，则计算可得加密后的报文为\(402\)，解密之后的报文为4583
P8
a.\(n=pq=55,z=(p-1)(q-1)=40\)
b.因为此时\(e<n\)且\(e\)和\(z\)互质
c.可计算出\(d=27\)
d.\(c=m^e\%55=8^3\%55=17\)
P9
a.\(S=(g^{S_A}\%p)^{S_B}\%p=g^{S_AS_B}\%p=(g^{S_B}\%p)^{S_A}\%p=S^{'}\)
b.和c.

• \(T_A=g^{S_A}\%p=10,T_B=g^{S_B}\%p=4\)
• \(S=T_B^{S_A}\%p=4^5\%11=1=S^{'}\)

d.

如上图，这样Alice、Bob就分别于Trudy建立了联系，于是Trudy就可以将两者的报文截下来进行简单解密了
P16
a.

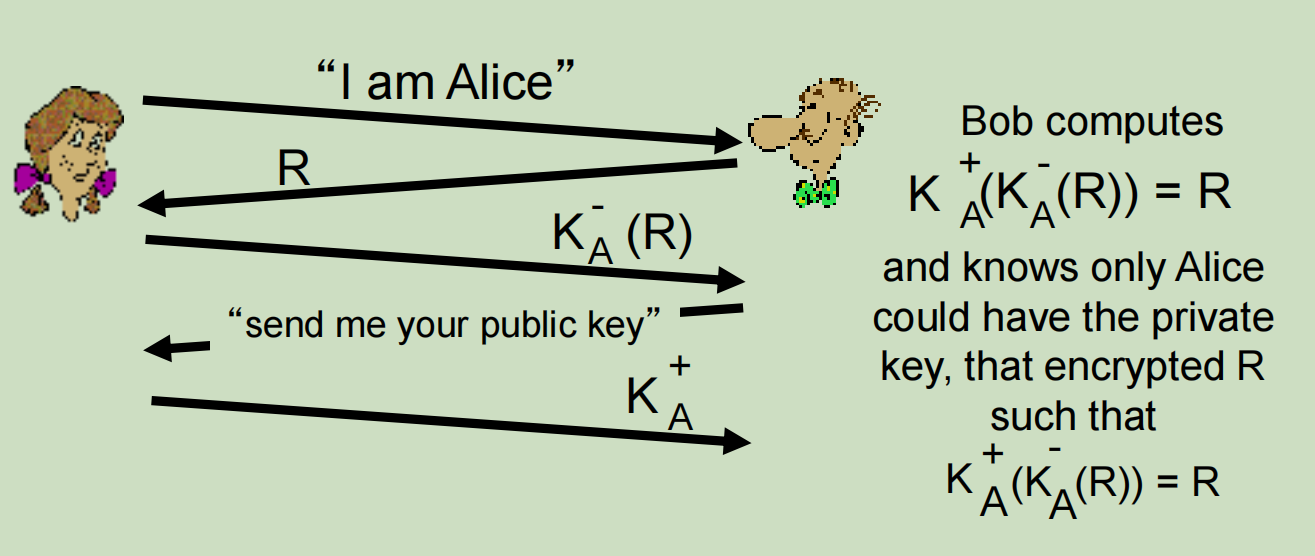
如课件所示
b.

如课件所示，由于没有签名，所以Bob不知道自己得到的公钥是不是Alice的，于是就被欺骗了，所以Trudy可以进一步地欺骗Alice
P18
a.不行，因为现在Alice没有任何东西只属于她，也就是说Alice可以干的事情Trudy都可以干，于是Bob没办法分辨到底是Alice发的还是Trudy发的
b.可以，因为现在只关心Alice发送的报文是否能够被Trudy所理解，于是直接将要发送的报文用Bob的公钥进行加密即可
P19
a.是客户发的
b.IP地址：216.75.194.220，端口号：443
c.为79+204=283
d.三个
e.包含一个加密主密匙
f.第一个字节：bc，最后一个字节：29
g.6
h.6
第九章：
P1
a.仅 1/4/5/6 号块准时播放。设第\(i\)个块准时播放，则需要满足在\(t_1+(i-1)△\)之前到达。从图中可以看出，只有这四个块满足
b.同理可得1-6 号块均准时播放，7 号超时
c.客户缓冲区容量为两个（完整的）块：3/4 号块在 (\(t_1+2△\), \(t_1+3 △\)) 到达并存在缓冲里，5 号块在(\(t_1+3△\), \(t_1+4 △\))到达时与 4 号一起存在缓存里
d.为保障所有块及时到达，最小播放起始时间需设为 \(t_1 + 3△\)。由之前的分析不难得出
P3
a. 服务器平均发送速率为 \(\dfrac{H}{2}\)
b.播放首帧后，因后续数据到达速率 \(x(t) < r\)（播放速率），下一帧无法按时到达，导致停滞
c.播放开始时间：\(t_p = \sqrt{\dfrac{2QT}{H}}\)（可通过积分算出），其中 \(Q\) 是播放触发阈值（缓冲区比特数），假设满足 \(\dfrac{HT}{2} \geq Q\)，这样在第一个周期就会进行播放，简化积分计算
d.从 \(t = T\) 开始播放后，可以推导出，对所有 \(t \geq 0\)，恒有 \(q(t+T) > 0\)，所以无停滞
推导如下：

\[\begin{align*} q(t+T) &= \frac{HT}{2} - rt + \int_{0}^{t} x(s) \, ds \\ &> \frac{H}{2}(T-t) + \int_{0}^{t} x(s) \, ds \\ &= \frac{H}{2}(T - nT - \Delta) + \frac{nHT}{2} + \frac{H\Delta^2}{2T} \\ &= \frac{H}{2}\left(T - \Delta + \frac{\Delta^2}{T}\right) \\ \end{align*} \]

当\(0 < ∆ < T\)时显然成立
e.设\(t_p\)是开始播放的时间，由d.可知，\(t_p\leq T\)
设\(q(t)=\frac{1}{2}\cdot\frac{Ht}{T}\cdot t-r(t-t_p),t_p\leq t\leq T\)，则可知当\(t=\frac{rT}{H}\)的时候\(q(t)\)最小；若要\(q(t)_{\min}\geq0\)，则有\(t_p\geq\frac{rT}{2H}\)，也就是说找到了下界
对于上面的下界，不难使用积分得出这个下界是一个符合条件的下界
f.假设缓冲区在 \(t \leq T\) 前达到上限 \(B\) 的方程：

\[\dfrac{H}{2T} t^2 - r\left(t - \sqrt{\dfrac{2QT}{H}}\right) = B \]

解上面这个方程即可
P5
a.\(N\times N=N^2\)
b.\(N+N=2N\)
P20

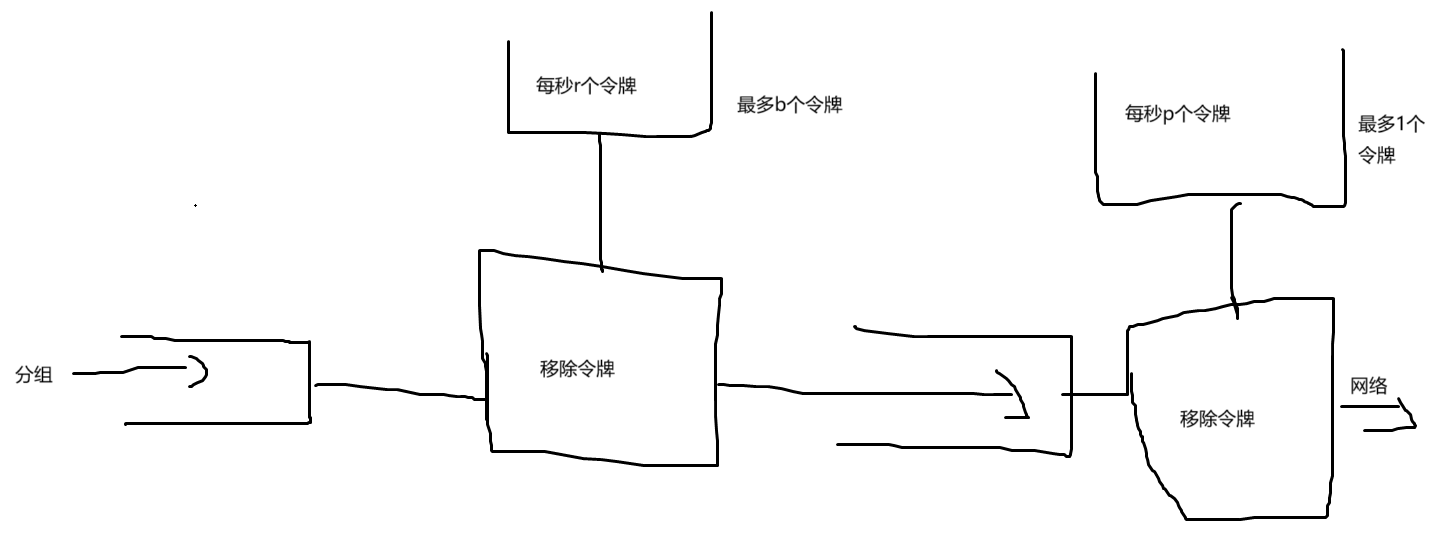
如上