15.2.1 使用循环神经网络表示单个文本

我们来想一下另一种方法的缺点：
一个简单的分类器如下

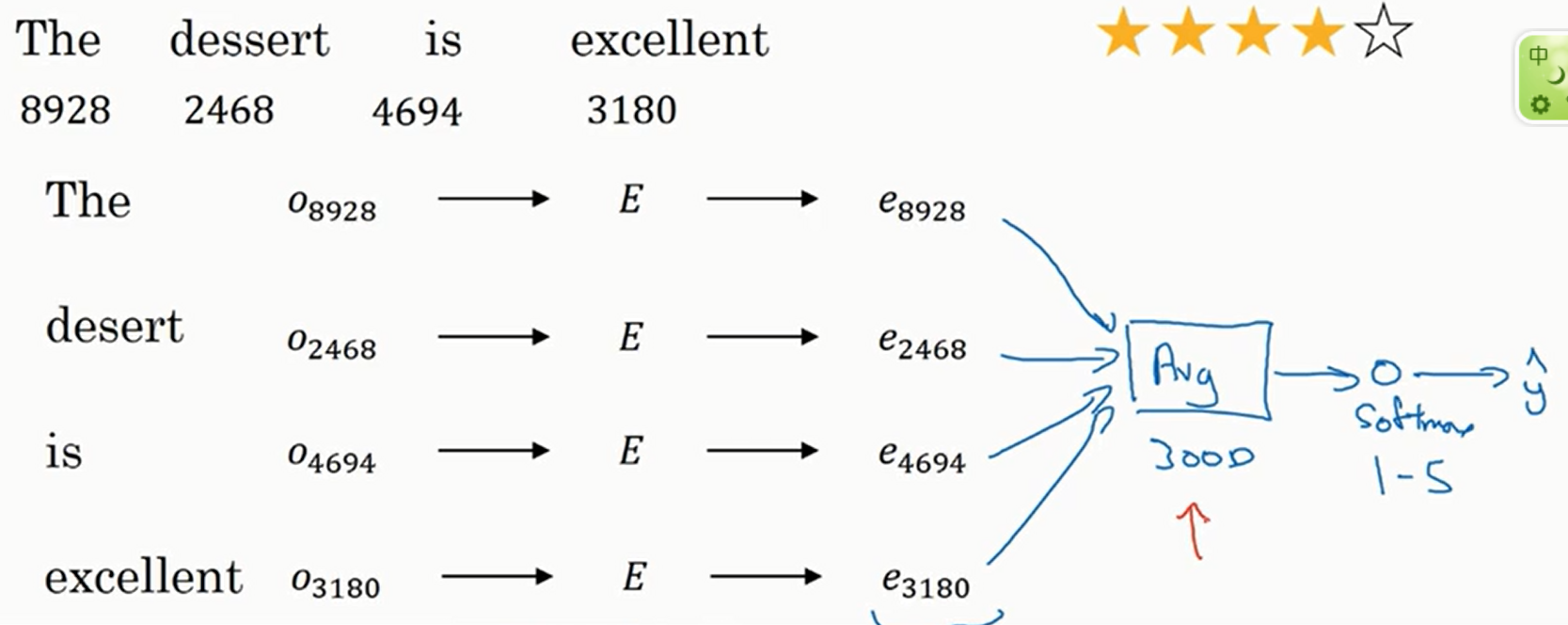
简单来说就是求出各个单词的\(e\)之后将他们加起来并平均然后传入\(\text{Softmax}\)层
这个算法有一个缺点就是忽略了单词的顺序，比如下面

这句话是一个很显然的负面评论，但是由于出现了很多次good，可能分类器会认为他是正面评论

在PyTorch中，当设置nn.LSTM的bidirectional参数为True时，输出包含以下三个部分：

1. 输出张量（output）

• 形状：(seq_len, batch, num_directions * hidden_size)
  • seq_len：序列长度。
  • batch：批量大小。
  • num_directions：方向数（双向时为2，单向时为1）。
  • hidden_size：每个方向的隐藏层大小。
• 内容：
  每个时间步的输出是正向和反向LSTM的隐藏状态的拼接。例如，若hidden_size=20，则输出的最后一个维度为40（正向和反向各占20）。

2. 最终隐藏状态（hn）

• 形状：(num_layers * num_directions, batch, hidden_size)
  • num_layers：LSTM的层数。
  • num_directions：方向数（双向时为2）。
• 内容：
  每个层和方向的最终隐藏状态。例如，若num_layers=2且bidirectional=True，则hn的形状为(4, batch, hidden_size)，其中：
  • 第0层正向隐藏状态：hn[0]
  • 第0层反向隐藏状态：hn[1]
  • 第1层正向隐藏状态：hn[2]
  • 第1层反向隐藏状态：hn[3]

3. 最终细胞状态（cn）

• 形状：(num_layers * num_directions, batch, hidden_size)
  与隐藏状态的形状一致。
• 内容：
  每个层和方向的最终细胞状态，结构与hn相同。

---

示例代码

import torch
import torch.nn as nn

# 定义双向LSTM
lstm = nn.LSTM(
    input_size=10, 
    hidden_size=20, 
    num_layers=1, 
    bidirectional=True  # 关键参数
)

# 输入数据：(seq_len=5, batch=3, input_size=10)
input = torch.randn(5, 3, 10)

# 前向传播
output, (hn, cn) = lstm(input)

# 输出形状
print(output.shape)      # torch.Size([5, 3, 40])  # 双向拼接后的结果
print(hn.shape)          # torch.Size([2, 3, 20])  # (num_layers*num_directions, batch, hidden_size)
print(cn.shape)          # torch.Size([2, 3, 20])

如何分离正向和反向输出？

# 分离双向LSTM的输出
forward_output = output[:, :, :20]  # 正向部分
backward_output = output[:, :, 20:] # 反向部分

---

总结

• 双向LSTM的输出：
  • output是正向和反向隐藏状态的拼接，维度为(seq_len, batch, hidden_size * 2)。
  • hn和cn的维度为(num_layers * 2, batch, hidden_size)，按层和方向排列。
• 适用场景：
  双向LSTM适用于需要同时捕捉序列前后依赖的任务（如文本分类、命名实体识别等）。

在双向LSTM中，output 是每个时间步的正向和反向隐藏状态（hidden states）的拼接。具体来说，对于序列中的每个位置（时间步），正向LSTM从左到右处理序列，反向LSTM从右到左处理序列，二者的隐藏状态在最后一个维度（特征维度）上拼接。

---

具体例子说明

假设有以下参数：

• 输入序列长度 seq_len = 3
• 批量大小 batch = 1
• 输入特征维度 input_size = 2
• 隐藏层大小 hidden_size = 2
• bidirectional = True

1. 输入数据

输入张量形状为 (3, 1, 2)，表示序列长度为3，批量大小为1，每个时间步的特征为2维：

input = torch.tensor([
    [[1.0, 2.0]],   # 时间步 0
    [[3.0, 4.0]],   # 时间步 1
    [[5.0, 6.0]]    # 时间步 2
])

2. 正向LSTM的输出

正向LSTM处理顺序：时间步 0 → 1 → 2。
每个时间步的隐藏状态（假设权重初始化为简单计算）：

• 时间步 0 的隐藏状态：[0.1, 0.2]
• 时间步 1 的隐藏状态：[0.3, 0.4]
• 时间步 2 的隐藏状态：[0.5, 0.6]

正向输出形状为 (3, 1, 2)：

正向输出 = [
    [[0.1, 0.2]],  # 时间步 0
    [[0.3, 0.4]],  # 时间步 1
    [[0.5, 0.6]]   # 时间步 2
]

3. 反向LSTM的输出

反向LSTM处理顺序：时间步 2 → 1 → 0。
每个时间步的隐藏状态：

• 时间步 2 的隐藏状态（反向初始）：[0.7, 0.8]
• 时间步 1 的隐藏状态：[0.9, 1.0]
• 时间步 0 的隐藏状态：[1.1, 1.2]

反向输出形状为 (3, 1, 2)，但按原始序列顺序排列：

反向输出 = [
    [[1.1, 1.2]],  # 时间步 0（反向处理后的结果）
    [[0.9, 1.0]],  # 时间步 1
    [[0.7, 0.8]]   # 时间步 2
]

4. 双向拼接后的输出

将正向和反向的隐藏状态在最后一维拼接，形状为 (3, 1, 4)：

双向输出 = [
    [[0.1, 0.2, 1.1, 1.2]],  # 时间步 0
    [[0.3, 0.4, 0.9, 1.0]],  # 时间步 1
    [[0.5, 0.6, 0.7, 0.8]]   # 时间步 2
]

---

如何分离正向和反向输出？

通过切片操作可以分离两个方向的输出：

# 正向部分：取前 hidden_size 个维度
forward_output = output[:, :, :2]

# 反向部分：取后 hidden_size 个维度
backward_output = output[:, :, 2:]

---

总结

• 拼接内容：每个时间步的正向和反向隐藏状态在特征维度（最后一维）拼接。
• 输出形状：(seq_len, batch, hidden_size * 2)。
• 适用场景：双向LSTM的拼接输出可以同时捕捉序列的前向和后向依赖关系，常用于文本分类、序列标注等任务。