10.5.2 实现

valide_lens是二维数组，假设其如下

tensor([[ 0,  1,  2,  3,  4],
        [ 5,  6,  7,  8,  9],
        [10, 11, 12, 13, 14],
        [15, 16, 17, 18, 19]])

那么对其在第零维进行repeat_interleave后，如下

tensor([[ 0,  1,  2,  3,  4],
        [ 0,  1,  2,  3,  4],
        [ 0,  1,  2,  3,  4],
        [ 5,  6,  7,  8,  9],
        [ 5,  6,  7,  8,  9],
        [ 5,  6,  7,  8,  9],
        [10, 11, 12, 13, 14],
        [10, 11, 12, 13, 14],
        [10, 11, 12, 13, 14],
        [15, 16, 17, 18, 19],
        [15, 16, 17, 18, 19],
        [15, 16, 17, 18, 19]])

对其在第一维执行后如下

tensor([[ 0,  0,  0,  1,  1,  1,  2,  2,  2,  3,  3,  3,  4,  4,  4],
        [ 5,  5,  5,  6,  6,  6,  7,  7,  7,  8,  8,  8,  9,  9,  9],
        [10, 10, 10, 11, 11, 11, 12, 12, 12, 13, 13, 13, 14, 14, 14],
        [15, 15, 15, 16, 16, 16, 17, 17, 17, 18, 18, 18, 19, 19, 19]])

可以结合下面的permute的讲解想一下为什么要在第零维这么执行

注意，reshape是不会改变数据在内存中的顺序的，而permute是会改变的，举例如下

x = tensor([[[ 0,  1,  2,  3],
           [ 4,  5,  6,  7],
           [ 8,  9, 10, 11]],
          [[12, 13, 14, 15],
           [16, 17, 18, 19],
           [20, 21, 22, 23]]])

如果执行y = x.permute(2, 0, 1)，那么有

y = tensor([[[ 0,  4,  8],
           [12, 16, 20]],
          [[ 1,  5,  9],
           [13, 17, 21]],
          [[ 2,  6, 10],
           [14, 18, 22]],
          [[ 3,  7, 11],
           [15, 19, 23]]])

如果再执行如下代码

cnt=0
for i in range(x.shape[0]):
    for j in range(x.shape[1]):
        for k in range(x.shape[2]):
            if x[i][j][k]!=y[k][i][j]:
                cnt+=1
cnt

会发现输出为\(0\)
我们来从几何上理解一下，在transpose_qkv中，我们忽略X的第零维，那么在permute之前，X是下面这个样子

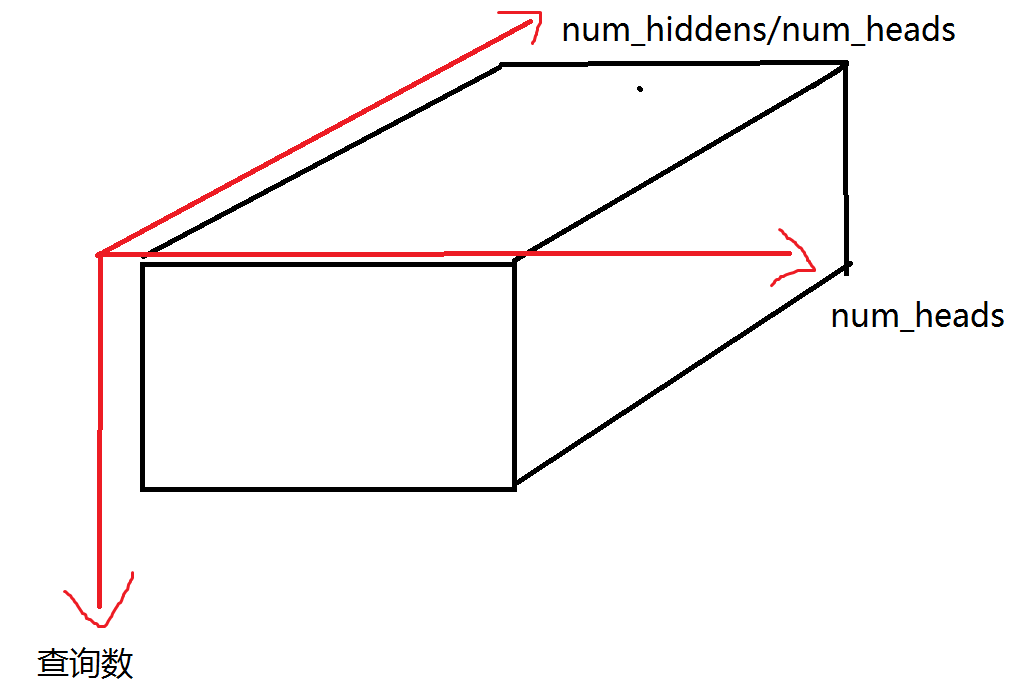
其中查询数是第零维，num_heads是第一维，num_hiddens/num_heads是第二维（想一下元素是怎么遍历的）；在permute之后，num_heads是第零维，查询数是第一维，num_hiddens/num_heads是第二维（想一下元素是怎么遍历的）