Problem Set 1
Problem Set 1.1
Problem 1.1.1
\(1)\)
基本情况:若\(z=0\),则\(yz=0\),返回正确值
归纳假设:令\(d\)为一个常数,假设\(\forall z<d\),算法返回正确值
归纳步骤:若\(z=d\),利用数学归纳法
- 若\(z\)为偶数,则返回\(\text{INT-MULT}(2y,\frac{z}{2})\),由于函数的第二个参数变小了,根据数学归纳法,有\(\text{INT-MULT}(2y,\frac{z}{2})=2y\cdot\frac{z}{2}=yz\),返回正确值
- 若\(z\)为奇数,则返回\(\text{INT-MULT}(2y,\frac{z-1}{2})+y\),由于函数的第二个参数变小了,根据数学归纳法,有\(\text{INT-MULT}(2y,\frac{z-1}{2})+y=2y\cdot\frac{z-1}{2}+y=yz\),返回正确值
\(2)\)
基本情况:若\(z=0\),则\(yz=0\),返回正确值
归纳假设:令\(d\)为一个常数,假设\(\forall z<d\),算法返回正确值
归纳步骤:若\(z=d\),利用数学归纳法。设\(z\space\text{mod}\space c=r\),则返回\(\text{INT-MULT}(cy,\frac{z-r}{c})+ry=yz\),返回正确值
Problem 1.1.2
由代码有\(T(n)=\frac{n/4}{n}\cdot10+\frac{2(n/2-n/4)}{n}\cdot20+\frac{3n/4-n/2}{2n}\cdot30+\frac{n-3n/4}{2n}\cdot n=16.25+\frac{n}{8}\)
Problem 1.1.3
\(1)\)
令\(U=\set{1,2,3,4},S=\set{\set{1,2,3},\set{4},\set{1,2}}\)
可知算法会选择会选择\(S\)的所有元素,但实际上只用选择两个元素即可
\(2)\)
使用深度优先搜索,考察\(S\)中每个元素是否选,一共有\(2^m\)种选择,将这些选择全部检查一遍,从符合题意的组合中选择组合包含元素个数最少的即可。由于覆盖了所有可能的情况,如果问题有解,那么肯定可以找出最小覆盖,也就是说算法是正确的。代码如下
void work(int step,int cnt)
//step表示当前正在选择第step个集合
//cnt表示已经选择的集合个数
{
if(step==m+1)
{
//now表示选择了的集合的并集
//ans表示最小覆盖数
if(now.size()==n) ans=min(ans,cnt);
return;
}
work(step+1,cnt);
set<int> now_copy=now;
for(set<int>::iterator it=s[step].begin();it!=s[step].end();++it)
now.insert(*it);
work(step+1,cnt+1);
now=now_copy;
}
\(3)\)
能,除非问题无解,比如令\(U=\set{1,2},S=\set{\set{1}}\)
Problem 1.1.4
以下代码均忽略数值溢出的问题
\(1)\)
int work(int T)//设S是全局变量,找到了返回最后一个被扫描到的硬币的下标,未找到返回0
{
int sum=0;
for(int i=1;i<=n;i++)
{
sum+=s[i];
if(sum==T) return i;
}
return 0;
}
反例:\(S=\set{1,2,3,4,5},T=4\)
\(2)\)
int work(int T)//设S是全局变量,找到了返回最后一个被扫描到的硬币的下标,未找到返回0
{
sort(s+1,s+n+1);
int sum=0;
for(int i=1;i<=n;i++)
{
sum+=s[i];
if(sum==T) return i;
}
return 0;
}
反例同\(1)\)
\(3)\)
int work(int T)//设S是全局变量,找到了返回最后一个被扫描到的硬币的下标,未找到返回0
{
sort(s+1,s+n+1,greater<int>());
int sum=0;
for(int i=1;i<=n;i++)
{
sum+=s[i];
if(sum==T) return i;
}
return 0;
}
反例同\(1)\)
Problem Set 1.2
Problem 1.2.1
\(1)\)
利用数学归纳法证明。
基本情况:有\(F_1=F_2=1,F_3=2\),可知,对于前三个数符合题意
归纳假设:设对前\(n\)个数符合题意(不妨设\(n\)是\(3\)的倍数)
归纳步骤:由于\(F_{n+1}=F_n+F_{n-1}\),而偶数加奇数为奇数,所以\(F_{n+1}\)为奇数,同理有\(F_{n+2}=F_{n+1}+F_n\)为奇数;有\(F_{n+3}=F_{n+1}+F_{n+2}\),而奇数加奇数为偶数,所以\(F_{n+3}\)为偶数。由于\(n\)是\(3\)的倍数,所以\(n+1,n+2\)不能被\(3\)整除而\(n+3\)可以,所以对于前\(n+3\)个数符合题意
\(2)\)
利用数学归纳法证明。
基本情况:对于\(F_1,F_2\),显然符合上述公式
归纳假设:假设对于前\(n-1\)个数符合上述公式
归纳步骤:要证明\(F_n^2 - F_{n+1}F_{n-1} = (-1)^{(n+1)}\),只用证明\(F_n^2 - (F_n+F_{n-1})F_{n-1}=(-1)^{(n+1)}\),而
证毕
Problem 1.2.2
\(1)\)
直接证明\(2)\)
\(2)\)
在二叉树中,有边数\(=\)总结点个数\(-1\)
而边数又等于子节点个数,所以子节点个数等于总结点个数\(-1\)
在这道题目中,即\(n_1+2n_2=n_0+n_1+n_2-1\)
化简即\(n_0=n_2+1\)
Problem 1.2.3
我认为题干的符号可能使用的不是很正确,像\(O\)这种符号都表示一个集合,而题干却让一个函数等于了一个集合,应该不是题目的意思,所以我认为等号应该换成\(∈\),下面仍然使用等号,但是表达\(∈\)的意思
\(1)\)
- O:若 $ f = O(g) $,则存在 $ c_1, n_1 $ 使得当 $ n \ge n_1 $ 时,$ f(n) \le c_1 g(n) $。若 $ g = O(h) $,则存在 $ c_2, n_2 $ 使得当 $ n \ge n_2 $ 时,$ g(n) \le c_2 h(n) $。取 $ n_0 = \max(n_1, n_2) $,当 $ n \ge n_0 $ 时,$ f(n) \le c_1 c_2 h(n) $,即 $ f = O(h) $
- Ω:类似 O,方向相反
- Θ:结合 O 和 Ω 的传递性,存在常数使得上下界同时传递
- o:若 $ f = o(g) $,则 $ \lim_{n \to \infty} \frac{f(n)}{g(n)} = 0 $。若 $ g = o(h) $,则 $ \lim_{n \to \infty} \frac{g(n)}{h(n)} = 0 $。故 $ \frac{f(n)}{h(n)} = \frac{f(n)}{g(n)} \cdot \frac{g(n)}{h(n)} \to 0 $,即 $ f = o(h) $
- ω:类似 o,极限趋向于无穷大,乘积仍趋向无穷大
\(2)\)
- O:取 $ c = 1 $,则 $ f(n) \le 1 \cdot f(n) $,故 $ f = O(f) $
- Ω:同理,$ f(n) \ge 1 \cdot f(n) $,故 $ f = Ω(f) $
- Θ:由 O 和 Ω 自反性,得 $ f = Θ(f) $
\(3)\)
- 自反性:已证
- 对称性:若 $ f = Θ(g) $,则存在 $ c_1, c_2 > 0 $ 使得 $ c_1 g(n) \le f(n) \le c_2 g(n) $,从而 $ \frac{1}{c_2} f(n) \le g(n) \le \frac{1}{c_1} f(n) $,即 $ g = Θ(f) $
- 传递性:已证
综上,Θ 是等价关系
\(4)\)
$ f = Θ(g) \iff f = O(g)∩Ω(g)\iff f = O(g),f = Ω(g)$
\(5)\)
- O与Ω:$ f = O(g) \iff \exists c > 0, f(n) \le c g(n) \iff g(n) \ge \frac{1}{c} f(n) \iff g = Ω(f) $
- o与ω:$ f = o(g) \iff \lim_{n \to \infty} \frac{f(n)}{g(n)} = 0 \iff \lim_{n \to \infty} \frac{g(n)}{f(n)} = \infty \iff g = ω(f) $
\(6)\)
- o(g) ∩ ω(g) = ∅:若 $ h \in o(g) $,则 $ \lim_{n \to \infty} \frac{h(n)}{g(n)} = 0 $,但若 $ h \in ω(g) $,则 $ \lim_{n \to \infty} \frac{h(n)}{g(n)} = \infty $,矛盾
- Θ(g) ∩ o(g) = ∅:若 $ h \in Θ(g) $,则 $ \exists c > 0 $ 使得 $ h(n) \ge c g(n) $,但 $ h \in o(g) $ 要求 $ h(n) \le \epsilon g(n) $ 对所有 $ \epsilon > 0 $,矛盾
- Θ(g) ∩ ω(g) = ∅:类似上一条
Problem 1.2.4
下面的小于符号和等于符号都代表渐进复杂度
\(1)\)
直接做\(2)\)
\(2)\)
Problem Set 1.3
Problem 1.3.1
第二个是正确的。对\(n=1,2\)显然成立
假设对前\(n-1\)项成立,那么\(F(n)=F(n-1)+F(n-2)\geq0.01(\frac{3}{2})^{n-1}+0.01(\frac{3}{2})^{n-2}=0.01(\frac{3}{2})^{n-2}\cdot\frac{5}{2}\geq0.01(\frac{3}{2})^{n}\)
第一个是不正确的,类似上面的正面,有\(\frac{5}{2}\leq\frac{9}{4}\),这显然是不对的
Problem 1.3.2
a.
有\(a=2,b=3,f(n)=1\),根据主定理,\(\exists \epsilon,f(n)∈O(n^{\log_ba-\epsilon})\),所以\(T(n)∈\Theta(n^{\log_ba})\)
b.
\(T(n)=c\log n+c\log\frac{n}{2}+c\log\frac{n}{4}+...+c\log 1=c\underset{k=0}{\overset{\log n}{\sum}}\log n-k∈\Theta(\log^2n)\)(用递归树也可以得到相同结果)
c.
有\(a=1,b=2,f(n)=cn\),根据主定理,\(\exists \epsilon,f(n)∈\Omega(n^{\log_ba+\epsilon})\),且有\(f(n/2)\leq\frac{3}{4}f(n)\),所以\(T(n)∈\Theta(n)\)
d.
有\(a=2,b=2,f(n)=cn\),根据主定理,\(f(n)∈\Theta(n^{\log_ba})\),所以\(T(n)∈\Theta(n\log n)\)
e.
\(T(n)=cn\log n+2\cdot c\frac{n}{2}\log\frac{n}{2}+4\cdot c\frac{n}{4}\log\frac{n}{4}+...+n\cdot c\log 1=cn\underset{k=0}{\overset{\log n}{\sum}}\log n-k∈\Theta(n\log^2 n)\)
f.
用递归树进行计算,如下
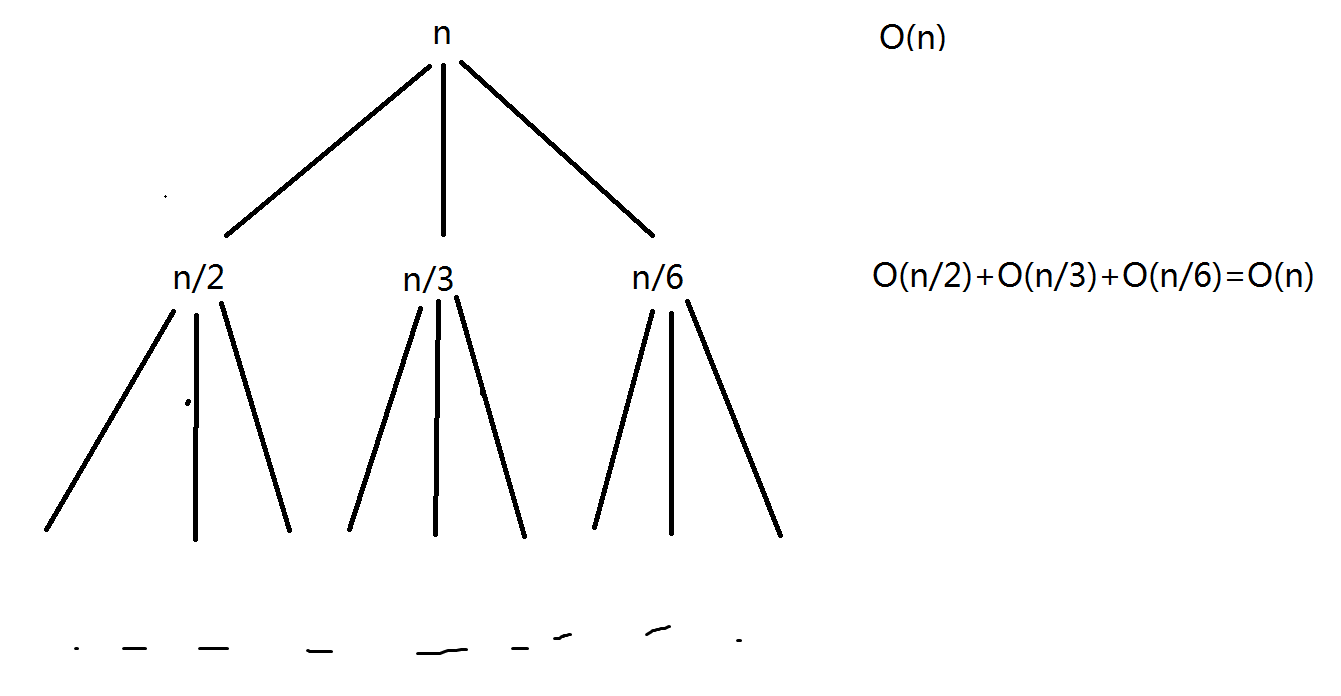
可以知道每一层的计算量都为\(O(n)\),一共有\(O(\log n)\)层,所以复杂度为\(O(n\log n)\)
注意这里的\(O(n)\)其实是\(cn\),因为在这个特殊场景下,算法是一样的,对于特定的输入\(n\),我一个确定的不变的算法能够执行的次数上界就是确定的
所以在这里可以像上面这个样子使用递归树或者替换法(而课后习题2.18就不能乱加);下一道题目同理
g.
利用递归树分析。对于第一层,总耗费为\(O(n)\);对于第二层,总耗费为\(O((a_1+a_2+...+a_k)n)\);对于第三层,总耗费为\(O((a_1+a_2+...+a_k)^2n)\);依此类推。由于\(a_1+a_2+...+a_k<1\),所以\(T(n)=O(n)\cdot\underset{i=0}{\overset{\infty}{\sum}}(a_1+a_2+...+a_k)^i=O(n)\)
也可以用代入法做,而且得出的结论更强。
假设\(T(n)\leq dn\),代入递归式得\(T(n)\leq d(a_1+a_2+...+a_k)n+cn\);要让\(d(a_1+a_2+...+a_k)n+cn\leq dn\),只需取\(d\geq\frac{c}{1-(a_1+a_2+...+a_k)}\),所以\(T(n)∈O(n)\);同理可证\(T(n)∈\Omega(n)\);所以\(T(n)∈\Theta(n)\)
当然这种形式也可以用递推法

Problem 1.3.3
仍然使用递归树分析,将\(\sqrt{n}T(\sqrt{n})\)看做\(\sqrt{n}\)个\(T(\sqrt{n})\)相加,可以知道每层的计算复杂度为\(\sqrt{n}O(\sqrt{n})=O(n)\),层数为\(n\)可以开根号的次数,设为\(m\),则时间复杂度为\(O(mn)\).\(m\)是一个很小的数,对于百万级别的数据来说,\(m\)不会超过\(10\),所以甚至可以视为一个常数
另外一种做法:\(T(n)=\sqrt{n}T(\sqrt{n})+n=\sqrt{n}(\sqrt{\sqrt{n}}T(\sqrt{\sqrt{n}})+\sqrt{n})+n=n^{3/4}T(n^{1/4})+2n\)
继续展开可以得到类似结论
Problem 1.3.4
(a)
最终的矩阵一共有四个元素,每个元素都是经过两次乘法运算和一次加法运算得到的,所以一共会经过八次乘法运算和四次加法运算;根据递推,不难得到,如果不使用矩阵快速幂而是使用\(O(n)\)的乘法的话,会经过\(8(n-1)\)次乘法运算
(b)
这个使用矩阵快速幂即可,数学原理是矩阵乘法满足结合律,代码见下
void mul(arr x,arr y)
{
ll z[1][2];
memset(z,0,sizeof(z));
for(int i=0;i<=0;i++)
for(int j=0;j<=1;j++)
for(int k=0;k<=1;k++)
z[i][j]=(z[i][j]+x[i][k]*y[k][j])%p;
memcpy(x,z,sizeof(z));
}
void mulself(arr x,arr y)
{
ll z[2][2];
memset(z,0,sizeof(z));
for(int i=0;i<=1;i++)
for(int j=0;j<=1;j++)
for(int k=0;k<=1;k++)
z[i][j]=(z[i][j]+x[i][k]*y[k][j])%p;
memcpy(x,z,sizeof(z));
}
int main()
{
n=read();
ans[0][0]=0,ans[0][1]=1;
ll A[2][2]={{0,1},{1,1}};
while(n)
{
if(n&1) mul(ans,A);
mulself(A,A);
n>>=1;
}
printf("%lld\n",ans[0][0]);
return 0;
}
(c)
要计算中间结果都是\(O(n)\)位长的,由于数列中的数都是正数,所以矩阵快速幂中间的矩阵的元素值不会比数列中的某些值大,所以只用证明\(F(n)\)的长度是\(O(n)\)的即可,即证明\(\log_{10}F(n)∈O(n)\).根据特征方程可以计算出\(F(n)\)的通项公式为\(\frac{\phi^n}{\sqrt{5}}\),于是不难证明
(d)
我们已经证明了会有\(O(\log n)\)次矩阵乘法,而每次矩阵乘法的复杂度为\(M(n)=O(n^2)\)(由(c),中间结果不会超过\(O(n)\)位),所以总的时间复杂度是\(O(M(n)\log n)\)
(e)
由提示,我们真正的复杂度其实是\(O(1^2)+O(2^2)+O(4^2)+O(8^2)+...+O((\frac{n}{2})^2)∈O(n^2)\),得证




 浙公网安备 33010602011771号
浙公网安备 33010602011771号