185 注意力模型（看不懂是什么模型，有空了重新看视频）

我们利用\(\text{GRU}\)或者\(\text{LSTM}\)构建一个双向循环神经网络如下

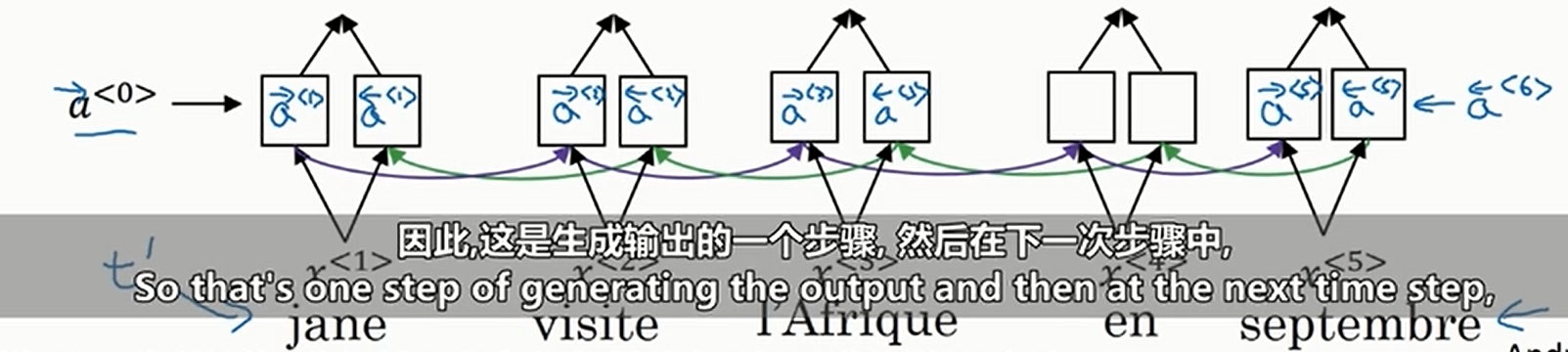
然后预测的时候我们使用普通的RNN，但是这个RNN的输入取决于源句子的每一个单词的加权和。我们用\(y\)表示预测的句子，\(a\)表示输入的句子，那么也就是说我们定义\(\alpha^{\left<t,t^{'}\right>}\)为\(y^{\left<t\right>}\)应该对\(a^{\left<t^{'}\right>}\)给予的“注意力”权重（由于这里使用的是双向神经网络，于是有\(a^{\left<t^{'}\right>}=\left(\overset{\rightarrow}{a}^{\left<t^{'}\right>},\overset{\leftarrow}{a}^{\left<t^{'}\right>}\right)\)），且满足\(\underset{t^{'}}{\sum}\alpha^{\left<t,t^{'}\right>}=1\)，示意图如下

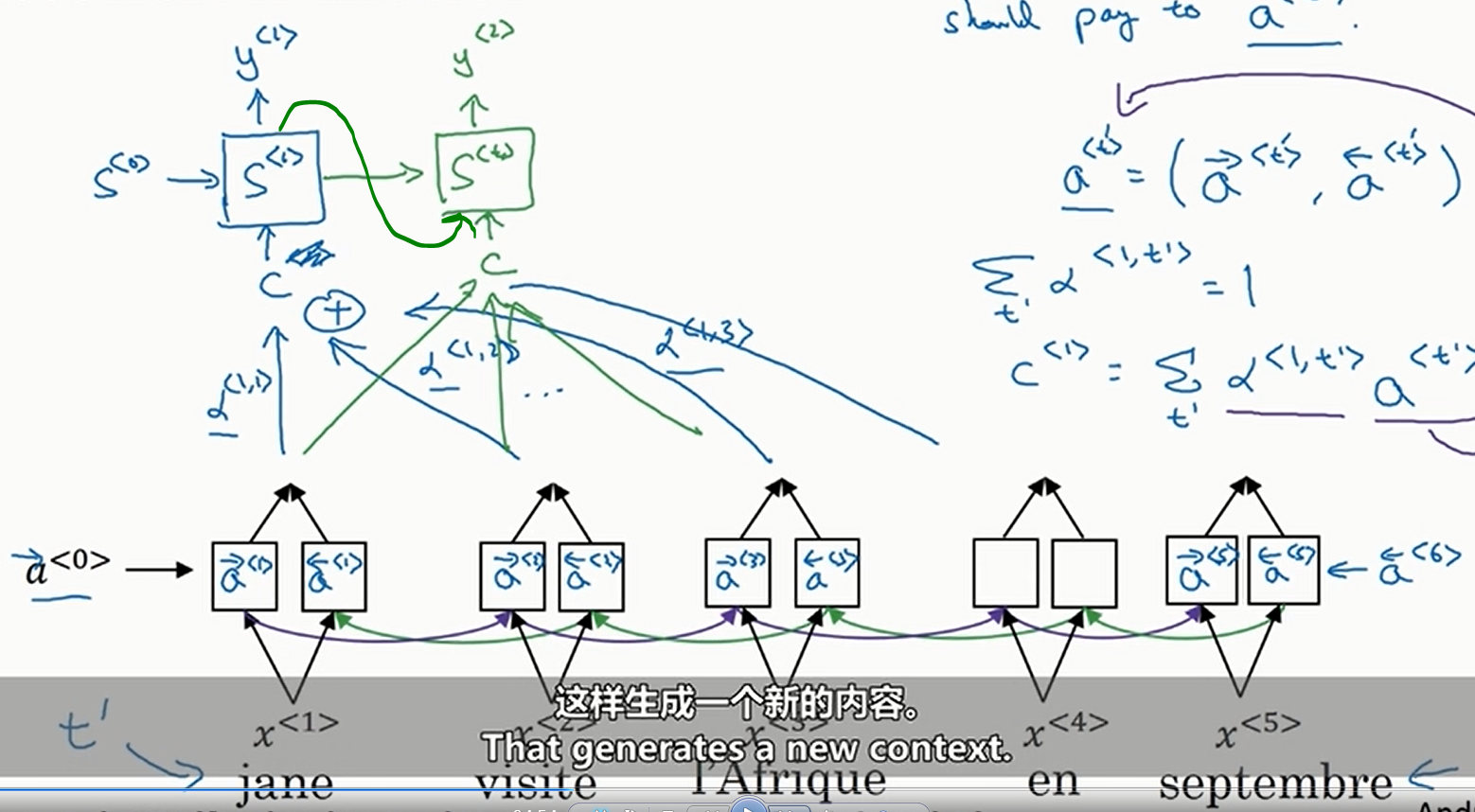
其中\(c^{\left<t\right>}=\underset{t^{'}}{\sum}\alpha^{\left<t,t^{'}\right>}a^{t^{'}}\)
那么怎么学习注意力权重呢？实际上，如下

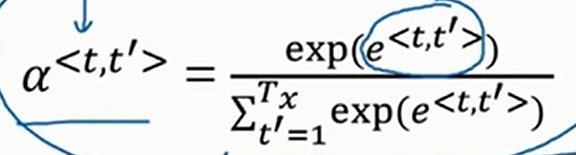
那么\(e^{\left<t,t^{'}\right>}\)跟什么有关呢？不难想到，跟RNN的上一时间步的隐状态\(s^{\left<t-1\right>}\)和输入的当前时间步单词\(a^{\left<t^{'}\right>}\)有关，但是我们不知道确切的函数，此时我们用一个小型神经网络去学习就好了。如下

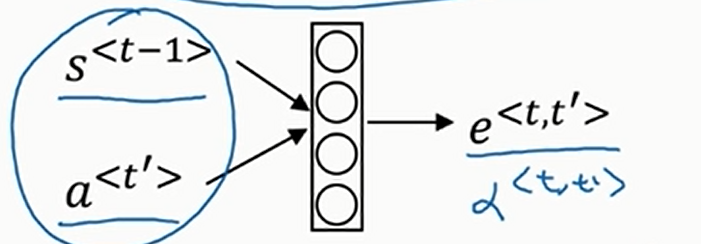
这就让注意力机制有了一个缺点，就是运行该算法需要二次时间或者二次成本（注意力权重参数个数等于输入句子的长度乘以输出句子的长度
可以画出热力图如下

不难看出，相对应的输入和输出单词的注意力权重很高