3.4.6 损失函数

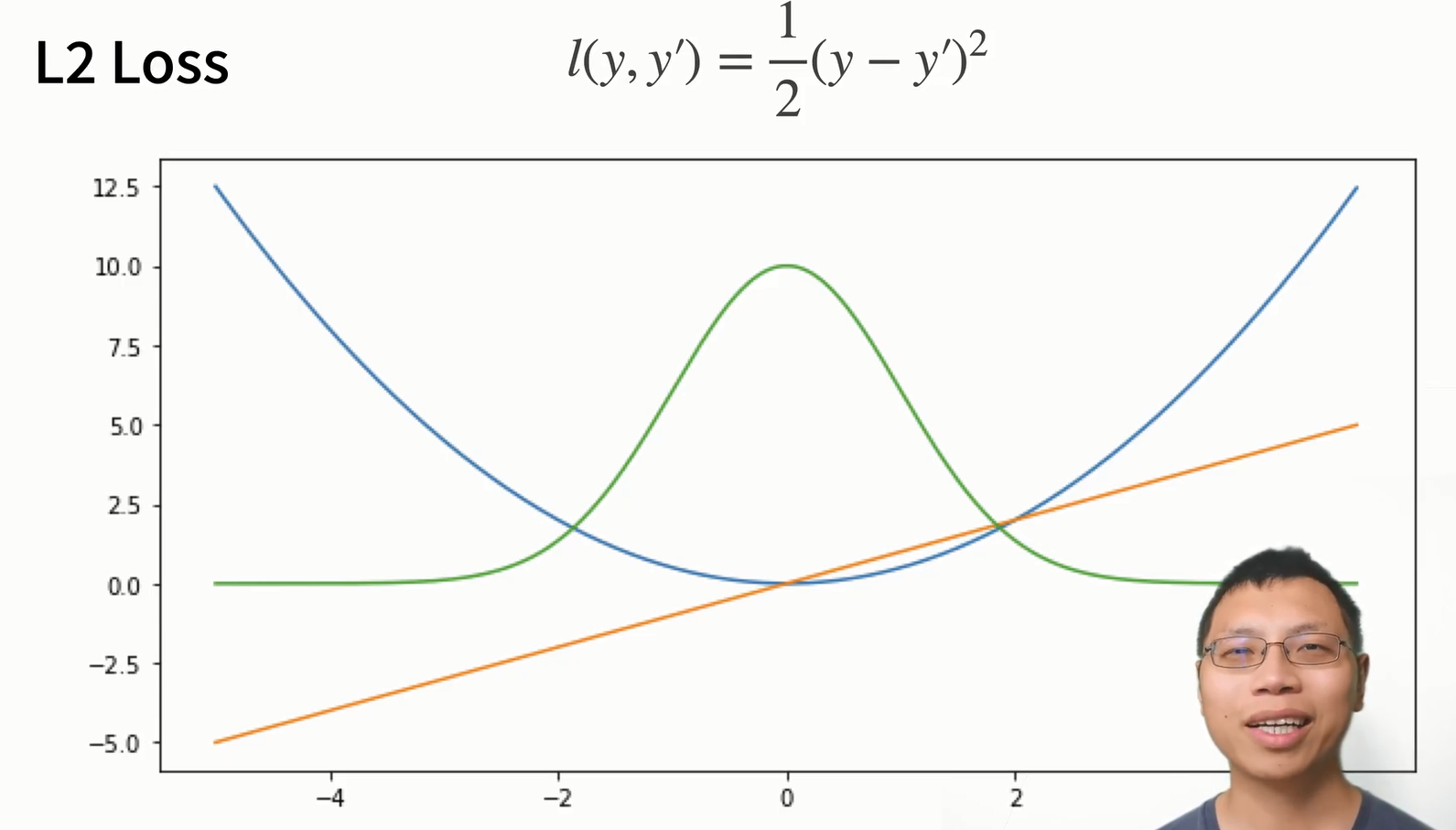
这个图的横坐标是\(y^{'}\)（认为\(y=0\)），纵坐标是函数值。蓝色曲线代表的是损失函数，绿色曲线代表的是似然函数的值（这里假设随机误差服从高斯分布），橙色曲线表示的是损失函数的梯度
这里可以发现，梯度的值是在变化的。前面提到过，我们不想要太大的梯度值，也不想要太小的梯度值，所以如果我们想要一个恒定的梯度值的话，可以使用\(L_1\)损失，如下

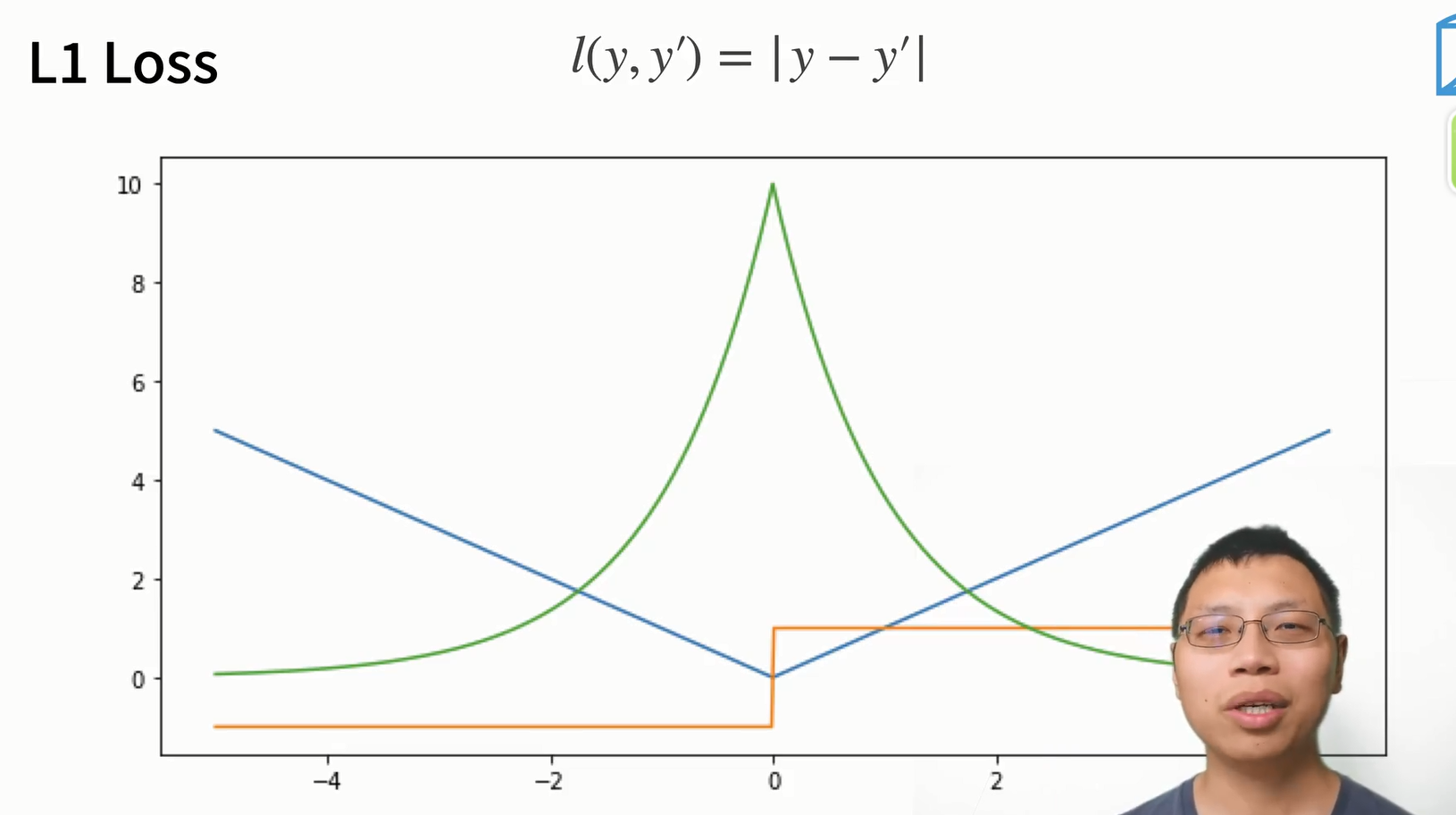
但是为啥绿色曲线是似然函数呢？似然函数不应该不变吗
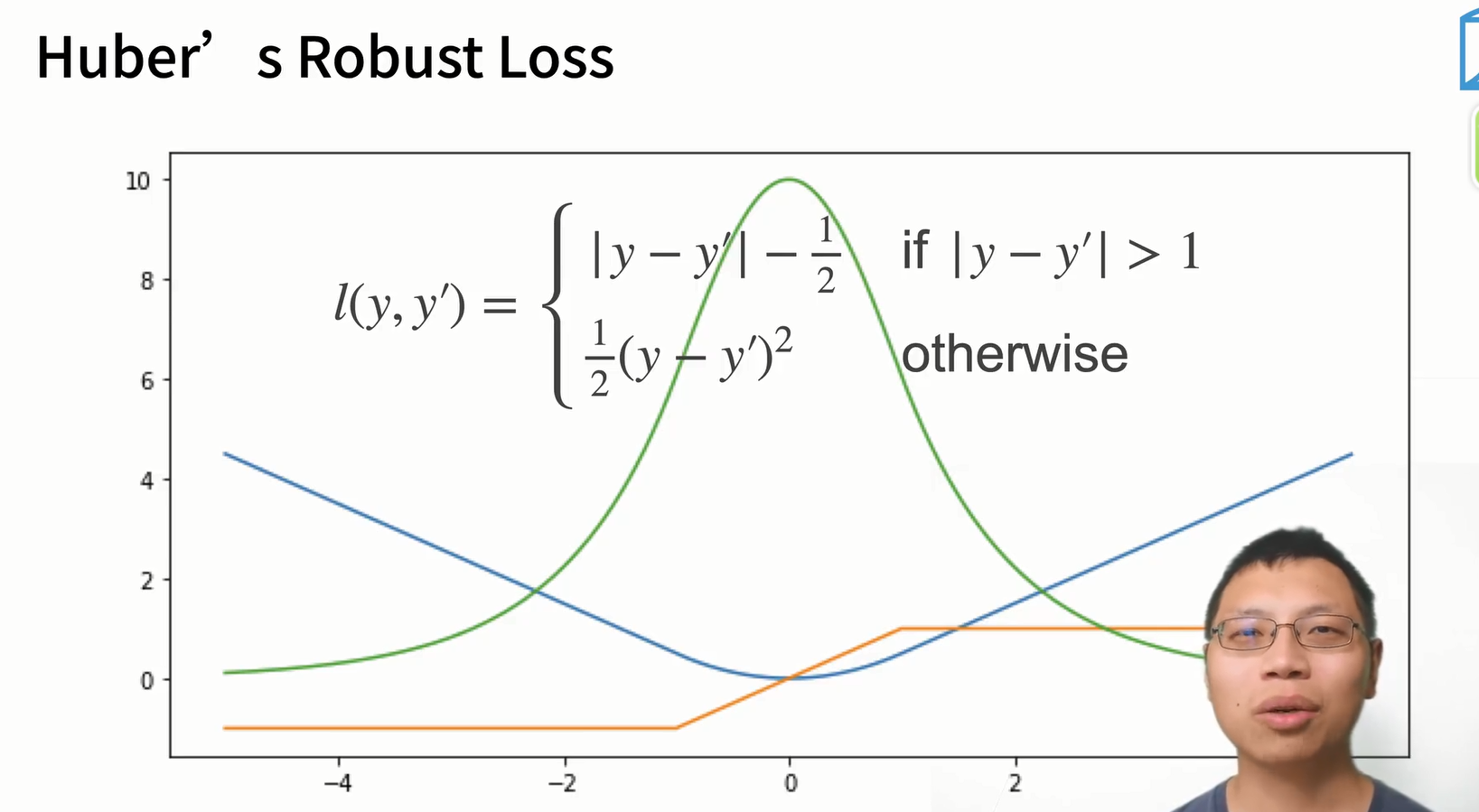
\(L_1\)损失可能出现迭代过慢的情况，我们可以结合\(L_1\)与\(L_2\)的优点，构建如下函数

式\((3.24)\)最后一个等号成立的原因：注意我们的\(\text{y}\)是独热编码，而\(\log P(\)\(\text{y}\)\(^{(i)}|\)\(\text{x}\)\(^{(i)})=\log \hat{y_y}\)，利用独热编码的性质可以知道，式\((3.25)\)只有一项存在，于是式\((3.24)\)成立
这里成立的原因是独热编码的性质。后面的“重新审视交叉熵”那一部分文字就没有认为\(\text{y}\)是独热编码，那个时候就不成立了
实际上，后面的代码实现，是按照独热编码实现的

书上式\((3.24)\)中\(l\)是式\((3.25)\)的原因：注意想一下极大似然法的过程，我们现在是有了参数，然后通过参数去（利用\(\text{softmax}\)）计算各个事件的概率，再去根据数据集估算这个数据集产生的概率并极大化。也就是说，设\(\hat{\text{y}}\)是我们估计的概率向量，那么有\(P(y^{(i)}|\text{x}^{(i)})=\underset{j=1}{\overset{m}{\prod}}\hat{y}_j^{y_j}\)，取对数即可。也就是说，交叉熵等价于极大似然估计