EK求最大流

代码见下

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1010,M=10010,inf=1<<29;
int End[M<<1],Next[M<<1],Len[M<<1],Last[N];
bool v[N];
int n,m,s,t,cnt=1,incf[N],pre[N];//注意cnt从1开始 
ll maxflow=0;
queue<int> q;
void add(int x,int y,int z)//最开始的流全为0，所以正向边为z反向边为0 
{
	End[++cnt]=y,Next[cnt]=Last[x],Len[cnt]=z,Last[x]=cnt;
	End[++cnt]=x,Next[cnt]=Last[y],Len[cnt]=0,Last[y]=cnt;
}
bool bfs()
{
	while(!q.empty()) q.pop();
	memset(v,0,sizeof(v));
	q.push(s),v[s]=1;
	incf[s]=inf;//incf[x]表示当前的残存网络上从s到x的路径的最小边长度 
	while(!q.empty())
	{
		int x=q.front();
		q.pop();
		for(int i=Last[x];i;i=Next[i])
		{
			int y=End[i],l=Len[i];
			if(!Len[i]||v[y]) continue;
			//若Len[i]为0表示这条边不存在于残存网络中，所以直接跳过 
			incf[y]=min(incf[x],l);
			pre[y]=i;//记录当前残存网络中y的前驱，之后好更新 
			q.push(y),v[y]=1;
			if(y==t) return 1;
		}
	}
	return 0;
}
void update()
{
	int x=t;
	while(x!=s)
	{
		int i=pre[x];
		Len[i]-=incf[t],Len[i^1]+=incf[t];//更新残存网络 
		x=End[i^1];
	}
	maxflow+=incf[t];
}
int main()
{
	scanf("%d%d%d%d",&n,&m,&s,&t);
	for(int i=1;i<=m;i++)
	{
		int u,v,c;
		scanf("%d%d%d",&u,&v,&c);
		add(u,v,c);
	}
	while(bfs()) update();
	printf("%lld",maxflow);
    return 0;
}

题目给的数据可能包含反向边，为什么我们不用像黑书说的先进行等价转化再去跑EK而是直接对原图跑EK呢？这是因为两个图在任意时刻的残存网络都是一一对应的：假设我们对两个图同时跑FF，那么两个图在任意时刻的残存网络都是一一对应的，比如下图

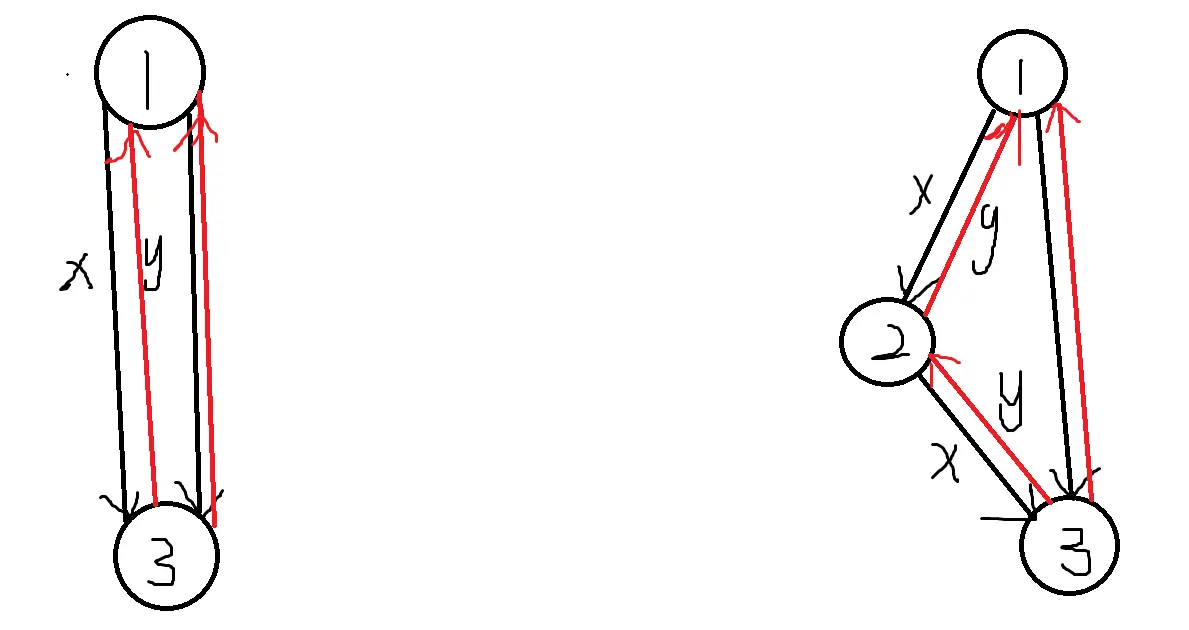
左边的图是题目给我们的图，右边的图是等价转化后的图（其中\(2\)是添加的点）；\(x,y\)是残存网络上的残存容量；两个图的\(x,y\)始终是相等的；黑色的边是原来的图就有的边，红色的边是残存网络添加的反向边

所以我们对图二跑FF，某一时刻找到了一条增广路，如果其包含\(1\rightarrow 2\rightarrow 3\)，那么我们就能够在图一中找到一条增广路，其包含\(1\rightarrow 3\)；而且由于\(x,y\)是相等的，我们更新之后新的残存网络仍然满足两个图一一对应；所以我们对图一跑FF就相当于对图二跑FF，而我们已经证明了图二跑FF是正确的，所以我们不用建立新点而是可以直接加入反向边