串珠子

置换群通常用来解决一些涉及「本质不同」的计数问题，例如用\(3\)种颜色给一个立方体染色，求本质不同的方案数（经过翻转后相同的两种方案视为同一种）

置换：将\(1,2,3,...,n\)映射到一个打乱之后的\(1\) ~ \(n\)的排列\(p_1,p_2,...,p_n\)。可以用一个函数来表示，\(f(p)=q\)（其中\(p,q\)是排列）。注意置换是函数\(f\)，而不是排列

循环置换：将\(1,2,3,...,n\)映射到\(2,3,4,...,1\)。如果建图，点\(i\)向\(i (\mod n) +1\)连边的话，会发现形成了一个环。若两个循环置换不含有相同的元素，则称它们是不相交的

置换的乘积：映射函数的复合

性质：任意一个置换都可以拆分成若干个不相交的循环置换的乘积

证明：对一个置换建图，从\(i\)向\(p_i\)连边，可以发现每个点的出度和入度都是\(1\)，所以这个图由若干个环构成，于是显然

置换群：对\(1\) ~ \(n\)的所有置换（一共有\(n!\)种）构成的集合是一个群，叫做置换群。不难验证置换群的子群也是置换群

群作用：与陪集一样，有左群作用和右群作用，下面以左群作用为例。设现有集合\(S\)和群\(G\)，如果存在一个映射\(\phi:G\times S\rightarrow S\)，满足以下条件：

1.\(\forall s∈S,\phi(e,s)=s\)（其中\(e\)是\(G\)中的单位元）

2.\(\forall g,h∈G,s∈S,\phi(gh,s)=\phi(g,\phi(h,s))\)

则称\(G\)作用在\(S\)上。

通俗来讲，就是对\(G\)中的每一个元素\(g\)，都构建一个映射\(\phi:S\rightarrow S\)满足\(\phi_g(x)=\phi(g,x)\)，并且单位元为恒等作用且乘积作用等于相继作用（也就是说对于一个属于\(S\)的元素\(s\)和两个属于\(G\)的元素\(g,h\)，先用\(g\)变换\(s\)再用\(h\)变换\(s\)的效果与直接用\(gh\)变换\(s\)的效果一样）

本质相同：设\(G\)作用于\(S\)。若\(x,y∈S\)，且存在\(g∈G\)，使得\(\phi_g(x)=y\)，那么就称\(x,y\)本质相同。

先证明本质相同关系是等价关系。定义本质相同关系\(R\)：\(xRy\iff\exists g∈G,\phi_g(x)=y\)

自反性：若\(s∈S\)，则\(\phi_e(s)=s\)

对称性：若\(x,y∈S\)且\(xRy\)，则\(\exists g∈G\)，使得\(\phi_g(x)=y\)，则\(\phi_{g^{-1}}(y)=\phi_{g^{-1}}(\phi_g(x))=\phi_{g^{-1}g}(x)=\phi_e(x)=x\)

传递性：若\(x,y,z∈S\)且\(xRy,yRz\)，则\(\exists g,h∈G\)，使得\(\phi_g(x)=y,\phi_h(y)=z\)，则\(\phi_{hg}(x)=\phi_h(\phi_g(x))=z\)

于是可以用\(S/G\)表示在\(G\)作用下的商集

Burnside引理：$$|S/G|=\frac{\underset{g∈G}{\sum}|S^g|}{|G|}$$

其中\(S^g=\left\{s|\phi_g(s)=s\right\}\)，也就是在\(g\)作用下不变的元素集合

Polya定理：是Burnside引理的一个具体应用，给出了特定情况下\(|S^g|\)的计算公式。设\(A,B\)是两个有限集合，\(S\)为\(A\)到\(B\)的所有映射组成的集合，\(G\)是作用在\(S\)上的置换群，则$$|S/G|=\frac{\underset{g∈G}{\sum}|B|^{c(g)}}{|G|}$$
，其中\(c(g)\)表示在\(g\)的作用下，将\(g\)拆分成若干个不相交的环的乘积之后，环的数量

置换群\(G\)作用在映射集合\(S\)上：比如\(s∈S,s=\left\{1\rightarrow1,2\rightarrow2,3\rightarrow1\right\}\)，则也许\(g(s)=\left\{1\rightarrow2,2\rightarrow1,3\rightarrow1\right\}\)。即保持定义域的顺序不变，变换值域的顺序

Polya定理也比较好理解，每个环的映射选择有\(|B|\)种，共有\(c(g)\)个环，所以有公式

一个具体的例子看OI-wiki

例子的解释看我们的：\(A\)是面的集合，标记为上下左右前后，\(B\)是颜色数量的集合，\(G\)就是置换群，题目要求我们算的就是等价类商集的大小

对于这道题目，有\(|A|=n,|B|=m\)，\(G\)一共有如下元素：

1.旋转：不妨全部设为顺时针旋转，于是有旋转的步数为\(k=0,1,2,...,n-1\)，此时我们要找出循环置换的个数，不难想到[SNOI2019] 数论一题的模型，可以知道循环置换的个数为\(\gcd(n,k)\)

2.翻转：此时要分情况讨论。如果\(n\)是奇数，那么一条对称轴长成下面这个样子：

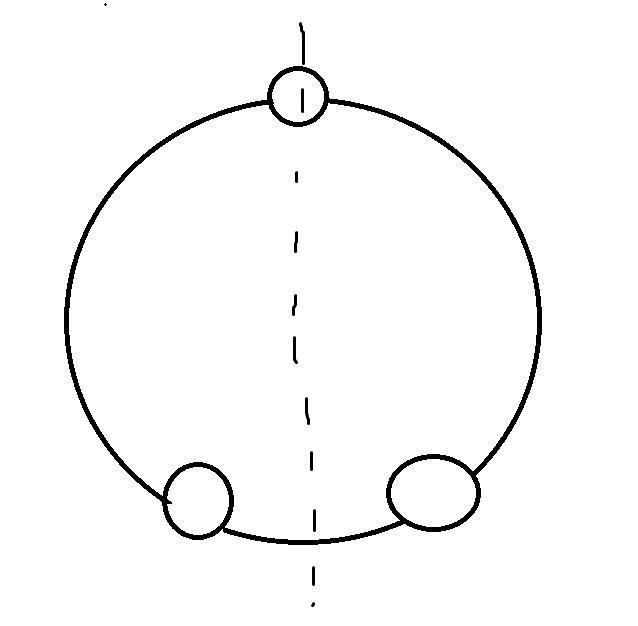
每条对称轴的循环置换的个数为\(\frac{n+1}{2}\)（注意包含自环），一共有\(n\)条这样的对称轴

如果\(n\)是偶数，那么一条对称轴长成下面两个样子：

第一个样子：

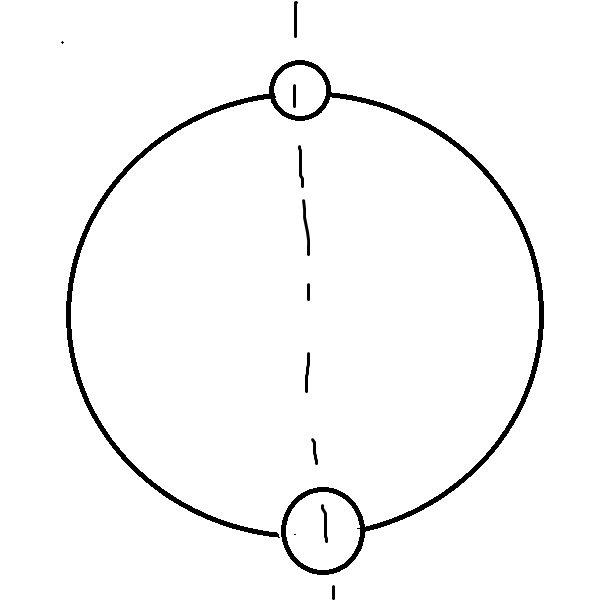
每条对称轴的循环置换的个数为\(\frac{n}{2}+1\)，一共有\(\frac{n}{2}\)条这样的对称轴

第二个样子：

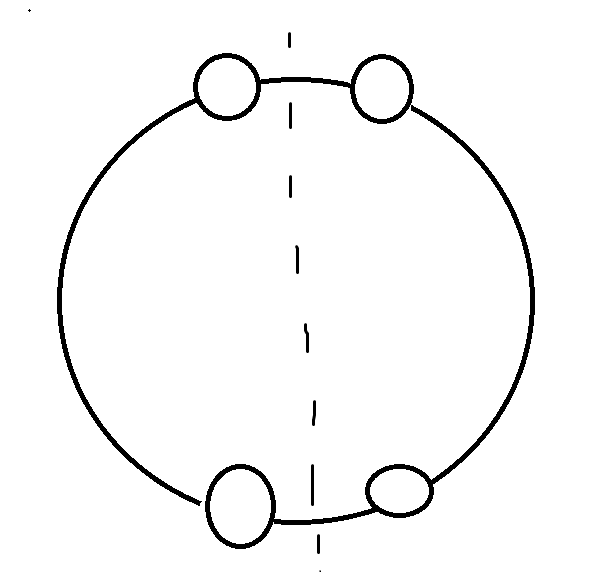
每条对称轴的循环置换的个数为\(\frac{n}{2}\)，一共有\(\frac{n}{2}\)条这样的对称轴

不难验证上面的\(G\)为群，于是就做完了