最小矩形覆盖

引理一：最小覆盖矩形的所有边上都有点，而且所有边都有凸包上的点，并且这条边上如果有多个点，那么这条边也是凸包的边

引理二：矩形的某一条边与凸包的某一条边共线

证明：反证。如果最小覆盖矩形没有边与凸包的边共线，那么根据引理一，矩形的每条边上有且仅有一个凸包上的点，如下图

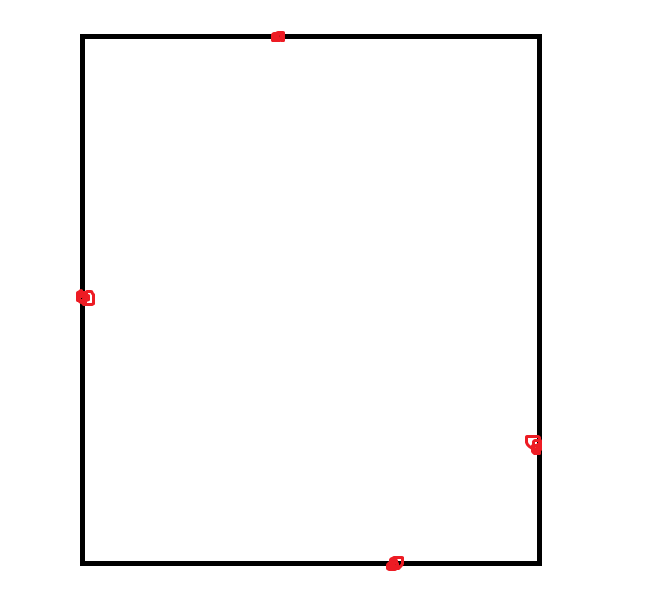
四个红色的点是凸包上的点

注意这是凸包，也就是说我们可以顺时针或逆时针旋转一个极小的角度，使得新的长方形的边上仍然只有这四个点，而此时由几何+函数可以证明，总有一个方向（要么是顺时针要么是逆时针）面积在减小，所以不可能

剩下的过程见OI-wiki

提醒一点，最后算坐标的时候，不要认为两个向量（设为\(\vec{a},\vec{b}\)）点乘可以直接得到\(\vec{b}\)在\(\vec{a}\)的投影的长度，而是还要除以\(\vec{a}\)的长度，因为这点调了好久