[JLOI2013] 赛车

对于\(i\)，存在\(t>0\)，使得对于任意\(j≠i\)，有\(k_i+v_it≥k_j+v_jt\)

这个时候别去化简了，化简了还没办法做，直接将\(k+vt\)看成一条直线，条件就转化成：如果\(i\)可以获奖，那么就可以找一条直线\(x≥0\)，使得这条直线上\(i\)的对应的方程的值最大，不难发现构成了一个半平面交。但是注意这个半平面交必须要在第一象限了，比如下图就不行

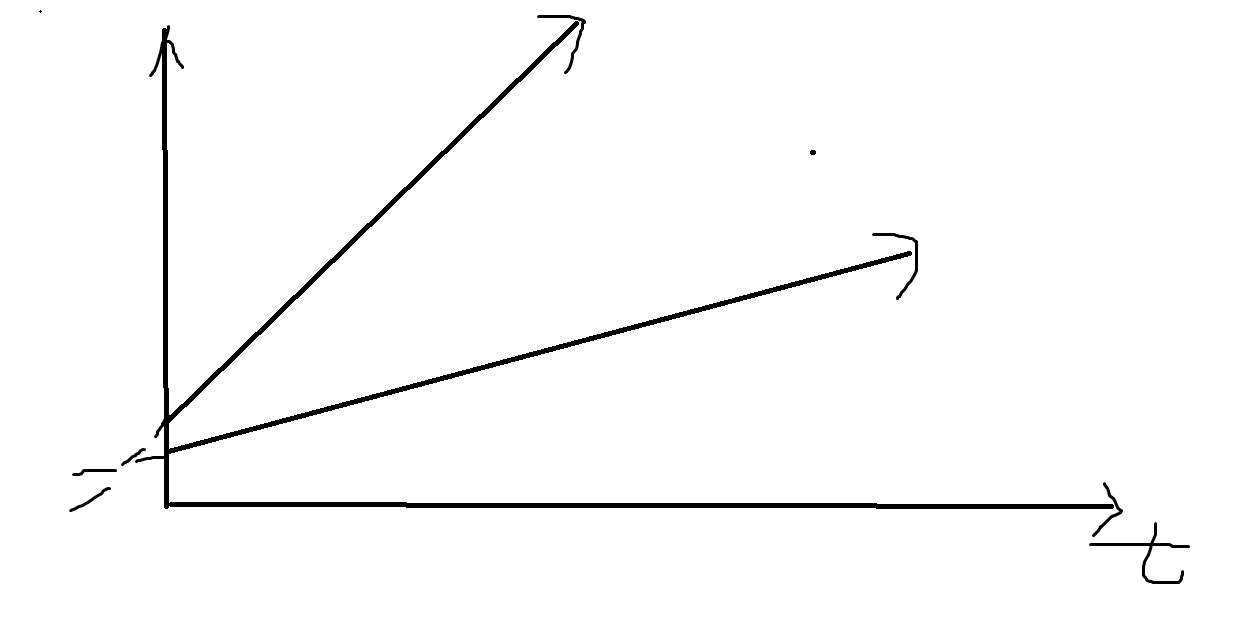
这种情况怎么避免呢？我们只用加入\(y\)轴反方向即可，再去求半平面交

再一个注意弹出队首队尾时，上一道题目求的是面积，所以在on_right函数中，如果area为\(0\)（也就是交于了一点），是可以弹出的，但这道题目就不行（只能没超过就能领奖，不用严格大于），所以这里要稍微改一下

然后是精度问题，要用long double，eps要为1e-18；但是有些\(0\)就不要改成eps了，比如on_right函数中的sgn函数后面的那个判断，sgn函数返回的是整型，这里跟精度没有关系，所以不要改