数表

我们首先直接根据题目列式子，对位置$(i,j)$，其在数表上的值为$$\sum _{n|i\mathrm{且}n|j}n$$，很显然就是$$\sum _{n|gcd(i,j)}n$$

我们先不考虑$a$的限制，题目的答案就是

$$\sum _{i=1}^n\sum _{j=1}^m\sum _{n|gcd(i,j)}n$$

，设$F(i)$表示$i$的约数和，答案就可以写成

$$\sum _{i=1}^n\sum _{j=1}^{m}F(gcd(i,j))$$

我们考虑$gcd(i,j)=k$的有多少对，这个时候就可以想起“破译密码”这道题目，答案就可以写成（除法都是整除）

$$\sum _{k=1}^{min(n,m)}F(k)\sum _{i=1}^{min(\frac{n}{k},\frac{m}{k})}u(i)\frac{\frac{n}{k}}{i}\frac{\frac{m}{k}}{i}=\sum _{k=1}^{min(n,m)}F(k)\sum _{i=1}^{min(\frac{n}{k},\frac{m}{k})}u(i)\frac{n}{ki}\frac{m}{ki}$$

现在考虑$a$的限制，我们发现当$F(k)>a$时，贡献为$0$，此时为了快速统计，可以离线，将询问按照$a$降序排序，然后每次将比当前$a$大的贡献清零，然后再数论分块。这里用树状数组就好了

但是这样仍然会超时，此时我们没有别的办法化简了，除了换序（所以以后没有别的办法的时候考虑换序）

如果不换序的话，是分块套分块，复杂度退化为$O(n)$；为了只分块一次，我们要将$\frac{n}{ki}\frac{m}{ki}$提到外面，所以我们令$ki=T$，将式子重写为

$$\sum _{k=1}^{min(n,m)}F(k)\sum _{k|T}u(\frac{T}{k})\frac{n}{T}\frac{m}{T}$$

这个时候要换序的话，跟微积分一样，先把所有函数写在一起，有

$$\sum _{k=1}^{min(n,m)}\sum _{k|T}F(k)u(\frac{T}{k})\frac{n}{T}\frac{m}{T}=\sum _{T=1}^{min(n,m)}\sum _{k|T}F(k)u(\frac{T}{k})\frac{n}{T}\frac{m}{T}$$

然后再把该提出的提出，有

$$\sum _{T=1}^{min(n,m)}\frac{n}{T}\frac{m}{T}\sum _{k|T}F(k)u(\frac{T}{k})$$

令$f(T)=\sum _{k|T}F(k)u(\frac{T}{k})$

原式可以写成

$$\sum _{T=1}^{min(n,m)}\frac{n}{T}\frac{m}{T}f(T)$$

预处理出$f$的前缀和就可以数论分块了

预处理$f$的话，可以用类似倍除法的思想，在$O(nlogn)$的时间内完成（也可以用线性筛，但是很麻烦，没必要）；然后注意仍然要倒序处理询问，而且每次处理的时候不是将某个$f$直接清空，而是清空某个$f$的一部分（因为更大的数的约数和不一定更大，而只有$F>a$了才会没有贡献）；然后还有注意写除法时一定要打括号。具体见以下代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e5+10,Q=2e4+10;
const ll mod=1ll<<31;
struct node
{
	int n,m,a,id;
}qry[Q];
int u[N],v[N],prime[N],cnt;
ll c[N],f[N],F[N],ans[N];
vector<int> pos[N*5];
void init(int n)
{
	u[1]=1;
	for(int i=2;i<=n;i++)
	{
		if(!v[i])
		{
			v[i]=i;
			prime[++cnt]=i;
			u[i]=-1;
		}
		for(int j=1;j<=cnt;j++)
		{
			if(prime[j]>v[i]||prime[j]>n/i) break;
			v[i*prime[j]]=prime[j];
			if(i%prime[j]==0||!u[i]) u[i*prime[j]]=0;
			else u[i*prime[j]]=-u[i];
		}
	}
}
bool cmp(node i,node j)
{
	return i.a>j.a;
}
void add(int x,int d)
{
	for(;x<=N-10;x+=x&-x) c[x]=(c[x]+d+mod)%mod;
}
ll ask(int x)
{
	ll res=0;
	for(;x;x-=x&-x) res=(res+c[x])%mod;
	return res;
}
int main()
{
	init(N-10);
	for(int d=1;d<=N-10;d++)
	for(int j=d;j<=N-10;j+=d)
	F[j]+=d;
	for(int d=1;d<=N-10;d++)
	for(int j=d;j<=N-10;j+=d)
	f[j]=(F[d]*u[j/d]+f[j])%mod;//倍除法 
	int Max=0;
	for(int i=1;i<=N-10;i++) 
	{
		pos[F[i]].push_back(i);
		Max=max(Max,(int)F[i]);
	}
	int q;
	scanf("%d",&q);
	for(int i=1;i<=q;i++)
	{
		scanf("%d%d%d",&qry[i].n,&qry[i].m,&qry[i].a);
		qry[i].id=i;
	}
	sort(qry+1,qry+q+1,cmp);
	for(int i=1;i<=N-10;i++)
	add(i,f[i]);
	for(int i=1;i<=q;i++)
	{
		while(Max>qry[i].a)
		{
			for(int j=0;j<pos[Max].size();j++) 
			for(int k=pos[Max][j];k<=N-10;k+=pos[Max][j]) 
			add(k,-F[pos[Max][j]]*u[k/pos[Max][j]]);
			//必须要这么清零，不能直接写成
			/*
			for(int j=0;j<pos[Max].size();j++) 
			add(pos[Max][j],-f[pos[Max][j]]);
			*/ 
			Max--;
		}
		for(int l=1,r;l<=min(qry[i].n,qry[i].m);l=r+1)
		{
			r=min(min(qry[i].n,qry[i].m),min(qry[i].n/(qry[i].n/l),qry[i].m/(qry[i].m/l)));
			ans[qry[i].id]=(ans[qry[i].id]+(ask(r)-ask(l-1)+mod)%mod*(qry[i].n/l)%mod*(qry[i].m/l)%mod)%mod;//注意后面两个(qry[i].n/l)和 (qry[i].m/l)一定要打括号，这样才能整除 
		}
	}
	for(int i=1;i<=q;i++) printf("%lld\n",ans[i]);
	return 0;
} 

上面的式子也可以按照莫比乌斯反演来考虑。由于题目没有出现$[gcd(i,j)=1]$，这个时候就要强行凑，所以我们枚举$gcd(i,j)$就好了，就可以写成下面这个样子

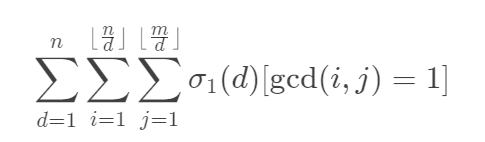
然后还有一个提醒的点是这里最后化出来的是莫比乌斯反演的第一形式，但是是分块套分块，会导致超时，这个时候就要利用莫比乌斯反演的第二形式，就是令$T=ki$这个操作，然后再将只与$T$有关的令成一个函数就好了

update 2024.8.5

为什么上面推导的时候我们要用$F(i)$去表示$i$的约数和，而不是直接将$\sum _{n|gcd(i,j)}n$写成$\sum _{n|i\mathrm{且}n|j}n$然后换序？

这其实是因为这道题目有$a$的限制，我们发现当$gcd(i,j)$固定的时候，$\sum _{n|gcd(i,j)}n$是一个定值，于是我们可以将求式写成

$$\sum _{i=1}^n\sum _{j=1}^m\sum _{n|gcd(i,j)}n[F(gcd(i,j))\le a]=\sum _{d=1}^{min(n,m,a)}F(d)\sum _{i=1}^n\sum _{j=1}^m[gcd(i,j)=d]$$

，然后就可以利用莫比乌斯反演了