传送带

建立函数按照这篇文章建立

但是证明这个函数是单峰的还是比较困难，我们只能来感性理解一下

我们首先将\(CD\)从线段变成直线，然后在\(F\)为无穷远的时候，函数值显然为无穷，然后我们把\(F\)拉到附近，函数值显然就为有限值了，再将\(F\)拉到另一端的无穷远，函数值又为无穷了，像这种一般都是三分，可以直接上三分了

update 2025.1.6

其实利用导数可以证明是三分的。假设我们现在已经固定了\(AB\)上面的一个点为\(E\)，我们现在要在\(CD\)上面找到一个点\(F\)，使得时间最短。我们不妨设\(D\)为坐标原点，\(DF\)为\(x\)轴，\(F(x,0),E(c,d)\)，于是所用的时间就是

\[f(x)=\frac{\sqrt{(c-x)^2+d^2}}{R}+\frac{|x|}{Q} \]

这个函数的一阶导和二阶导见下

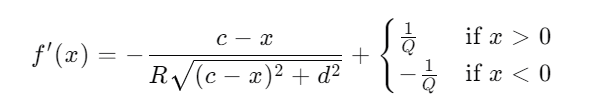
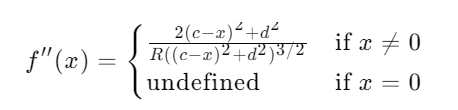
显然二阶导是大于\(0\)的，也就意味这一阶导是单调递增的；显然当\(x\to+\infty\)时，\(f^{'}(x)\to\frac{1}{R}+\frac{1}{Q}\)，当\(x\to-\infty\)时，\(f^{'}(x)\to-(\frac{1}{R}+\frac{1}{Q})\)，所以可以证明这是一个凹函数