小铃的烦恼

很显然，这道题目可以借助“分手是祝愿”这道题目的思想

我们尝试寻找不变量。

从只有两种属性的情况开始讨论，发现我们只要记录其中一种魔法属性有多少个就好了

但是如果有更多种魔法属性呢？我们不可能将所有颜色的属性的个数都记录下来，这样时间复杂度肯定会爆炸。但是我们可以仍然借助之前的思想，就只考虑某一种颜色，把这种颜色作为最终的目标颜色来推导

但是注意，我们不能直接设出\(f[i]\)表示当前有\(i\)个目标颜色的期望。因为从这个实验来看，任何一种颜色都有可能是最终颜色，我们的期望值不能单单仅局限于这一个目标颜色来算

如果我们直接设出\(f[i]\)表示当前状态有\(i\)个最终状态的字符，达到最终状态的期望步数

于是我们有

\[f[i]=1+\frac{A_{n-i}^2}{A_n^2}f[i]+\frac{A_{i}^2}{A_n^2}f[i]+\frac{A_{i}^1A_{n-i}^1}{A_n^2}f[i+1]+\frac{A_{i}^1A_{n-i}^1}{A_n^2}f[i-1] \]

然后你就会发现推不走了。因为你觉得\(f[0]\)为多少呢？正无穷？就算我采用“分手是祝愿”这道题目的定义方法，仍然逃不过这个问题。但是如果\(f[0]\)为正无穷的话，根据公式\(f\)都为正无穷，显然不可能

究其原因就是整个实验不是局限于某一种颜色的

那此时怎么办呢？我们发现，期望不能这么算（实际上，此时为条件期望，下面讲），但是概率还是可以这么算的，设\(p_i\)表示此时有\(i\)个目标颜色，最终颜色为目标颜色的概率

有

\[p_i=\frac{A_{n-i}^2}{A_n^2}p_i+\frac{A_{i}^2}{A_n^2}p_i+\frac{A_{i}^1A_{n-i}^1}{A_n^2}p_{i+1}+\frac{A_{i}^1A_{n-i}^1}{A_n^2}p_{i-1} \]

化简就是$$p_i=\frac{p_{i-1}+p_{i+1}}{2}$$

显然\(p_0=0,p_1=1\)，于是有\(p_i=\frac{i}{n}\)

条件期望：现有随机试验和两个随机变量\(X,Y\)，则\(E[X|Y=y]\)表示在\(Y=y\)发生的情况下，\(X\)的期望。形式化地，

\[E[X|Y=y]=\underset{x}{\sum}xP(X=x|Y=y) \]

全期望公式：

\[E[X]=E[E[X|Y]]\\=\underset{y}{\sum}P(Y=y)E[X|Y=y]\\=\underset{y}{\sum}P(Y=y)\underset{x}{\sum}xP(X=x|Y=y)\\=\underset{y}{\sum}P(Y=y)\underset{x}{\sum}x\frac{P(X=x∩Y=y)}{P(Y=y)}\\=\underset{y}{\sum}\underset{x}{\sum}xP(X=x∩Y=y) \]

对于这道题目，\(X\)则为实验的操作次数，\(Y\)则为实验的最终颜色，求的即\(E[X]\)；由全期望公式，设\(E_y=\underset{x}{\sum}xP(X=x∩Y=y)\)，则\(E[X]=\underset{y}{\sum}E_y\)。由于\(y\)是有限的，此时只用求出每个\(E_y\)即可

那么我们不妨画一个大致的样本空间图

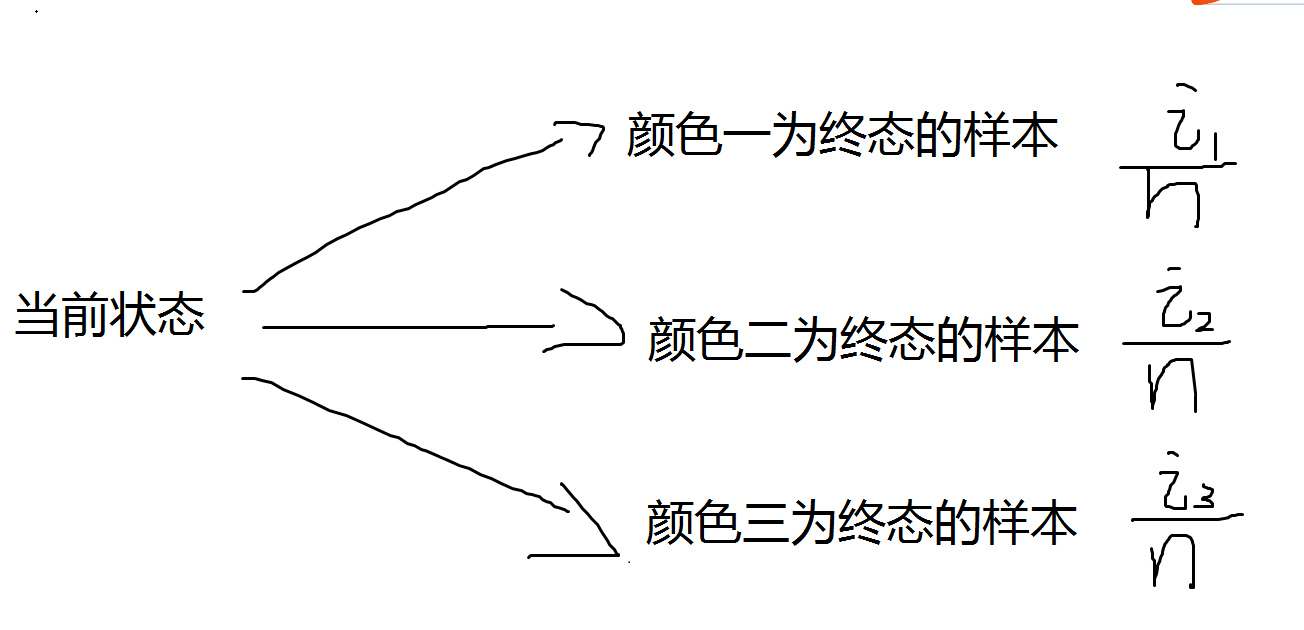
我们以颜色一为终态来举例。为了方便，将上文的\(E_y\)拓展一维变成\(E_{i,y}\)表示颜色\(y\)为最终颜色且当前有\(i\)张的期望，则\(E[X]=\underset{y}{\sum}E_{i_y,y}\)（\(i_y\)就是最开始的情况颜色\(y\)的个数）。那么\(E_{i_1,1}=\sum p_i^{'}d_i\)，其中\(p^{'}\)是每一个样本的概率，\(d\)是每一个样本的次数（想一下为什么\(E_1\)等于这个式子）

那么我们来考虑某一个样本，从当前这个情况，我们有\(\frac{i(n-i)}{n(n-1)}\)的概率让颜色一少一，此时从条件概率理解，就进入了另一种状态，这个状态有\(p_{i-1}\)的概率让颜色一成为目标颜色，假设在此时，所有的让颜色一成为目标颜色的样本的概率分别为\(p^{''}\)，那么有\(\sum p^{''}=p_{i-1}\)，所以这一种状态对\(E_1\)的贡献就是\(\frac{i(n-i)}{n(n-1)}\sum p^{''}(d^{''}+1)=\frac{i(n-i)}{n(n-1)}(E_{i_1-1,1}+p_{i-1})\)；让颜色一不变和颜色一多一的两部分的贡献同理；\(E_{i_1,1}\)就是三个部分贡献的和

注意到，

\[E_{i_1,1}=\underset{x}{\sum}xP(X=x∩Y=1)\\=P(Y=1)E_{i_1}[X|Y=1] \]

为了方便，设\(f[i]=E_i[X|Y=1]\)（\(i\)表示最开始有\(i\)张颜色一）

最终就可以化简得到$$f_i=\frac{(i-1)f_{i-1}+(i+1)f_{i+1}}{2i}+\frac{n^2-n}{2i(n-i)}$$

此时就不用关注\(f_0\)了，因为\(f_0\)的系数为\(0\)