NKOJ 2040

我先说一下我自己的想法，我觉得是对的，但是没有OJ验证不了

我们考虑第一种颜色的棋子，先放他，假设放完后，这种棋子占用了\(p\)行\(q\)列（任意的\(p\)行\(q\)列，显然不影响答案），则这\(p\)行\(q\)列就不能放其他棋子了，棋盘就剩下了\(n-p\)行\(m-q\)列

如果我们已经知道了剩下所有棋子放在\(n-p\)行\(m-q\)列上的方案数，我们再计算出第一种颜色的棋子占用了\(p\)行\(q\)列的方案数，两者乘起来，再乘以组合数\(C_n^p\)和\(C_m^q\)，是不是就是答案了？

于是整体框架就是记忆化搜索了，接下来是求某种颜色的棋子占用了\(p\)行\(q\)列的方案数

然后就结束了

但是PPT上面的做法，是利用另一个函数\(g\)过度

最终答案：

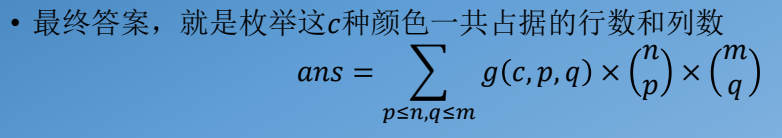
update 2024.9.13

我的那种做法是对的，其实本质上跟PPT的做法是一样的，只不过PPT用\(g\)来记录了一个状态而已，我们的记忆化搜索也要用类似的函数去记录的

重新做了一遍这道题目，没有想到的原因就是因为误认为一个颜色最多只会占一行一列了，此时就以这一行一列的交叉点为代表元素进行计数了；想明白这道题目一种颜色可以占多行多列之后，我们的思考对象肯定就是行和列了，于是从上面的角度进行思考。注意解题的过程中我们产生了若干个子问题，子问题一定要学会用状态标注，对于每个子问题，都有两种方法可以计算；这道题目还透露出一种非常重要的思想，就是我们在确定\(p\)行\(q\)列的时候，不用精确具体的哪\(p\)行\(q\)列，算出来的结果都是一样的（如果要精确到具体的话，时间复杂度就太大了）