捉迷藏

这里主要是对蓝书上做法的补充

首先看到这道题目，我们假设已经知道要选哪些点了，那我们在原图\(G\)上每选一个点，与这个点有关的路径上的所有点都要被打上标记，打上标记的点就不能再选了，所以我们选的点就是每次都没有标记的点

像这种“与一点有关的所有路径的所有点”，可以通过传递闭包后转化为“与一点走一条边有关的所有点”来简化，这就是为啥后面的分析是基于\(G^{'}\)的

然后蓝书上\(path\)的具体构造方案其实就是上一页证明里面的构造方案（二分图中的匹配边都选上）

我们是怎么想到最开始选终点的？我们考虑传递闭包之后的图，一般长成这个样子

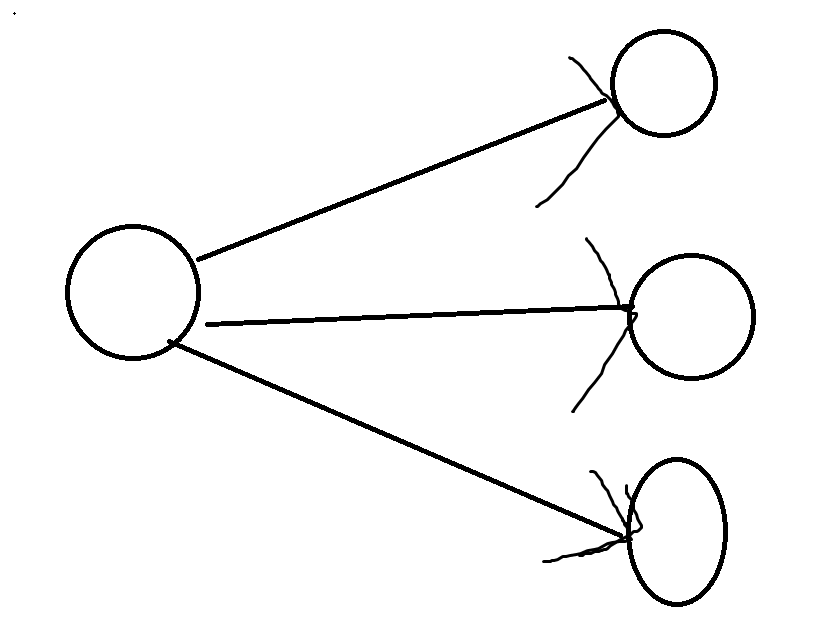
我们选择点，似乎是往终点选择更好，所以我们最开始先选上所有终点

然后我们让所有终点向前（注意是向前，不是向后）走一条边（注意这个边都是指\(G^{'}\)的边，而不是\(G\)的），就有了蓝书的第三步

然后蓝书说的\(e\)所在的路径\(pe\)指的是\(path\)中的一条路径\(pe\)；由于\(path\)是不相交的，所以对于\(E∩next(E)\)的每个节点的\(pe\)都是没有重复的点的

然后蓝书说的反证就是如果找不到\(e^{'}\)，那么\(E\)中的某一点就可以到达\(pe\)的起点，然后就可以把这两条路径给接起来，让\(path\)减少

注意\(next(E)\)在以上过程中是一直不变的，即就是最开始选的所有终点走一条边所求出来的\(next(E)\)

然后最后我们证明一下最终的点集是符合题意的

首先，在最终的点集中，对于没有更换的点（即最开始就选出来的终点），他们走一步显然是不能互相到达的，而且也不能到达某一个\(e^{'}\)（任意一个\(e^{'}\)都不在\(next(E)\)中，而现在由于最开始选出来的终点变少了，如果现在让这些终点走一条边形成一个集合\(next^{'}(E)\)，那么这肯定是\(next(E)\)的子集，所以\(e^{'}\)也不会是\(next^{'}(E)\)中的某一个元素）

然后对于某一个\(e^{'}\)，如果他能到达某一个没有更换的点，那么他肯定能到达\(next(E)\)中的某一个点，这就矛盾了。如果某一个\(e^{'}\)可以到达另一个\(e^{'}\)，那么前者一定能到达后者在其\(pe\)上的终点，也就能到达\(next(E)\)，也矛盾了

所以最终的点集是符合题意的

update 2024.8.24

蓝书的构造方法的证明有逻辑漏洞（这个构造方法不知道对不对，但是证明是不正确的）：从蓝书提供的代码来看，不应该是重复步骤\(3\) ~ \(4\)，而是应该重复步骤\(2\) ~ \(4\)，也就是说\(\text{next}(E)\)是要变化的，那么完全有可能，\(y_0\)是被一条路径\(P\)的中间某个点到达的，而不是\(P\)的终点到达的，所以\(y_0\)这条路径就不能被替代

但是不看构造的话，题目给出的结论是正确的。

反链：偏序集中的一个子集\(B\)，满足\(B\)中任意两个元素都不可比，即任意非空子集都不是全序集

Dilworht定理：对于任意有限偏序集，其最大反链中元素的数目必等于最小链划分中链的数目。此定理的对偶形式亦真，它断言：对于任意有限偏序集，其最长链中元素的数目必等于其最小反链划分中反链的数目。

这道题目肯定就是求最大反链了，而最小链划分肯定就是求最小路径点覆盖了，于是结论正确