连通图

补集思想转化见蓝书

这里主要讲一下另一种递推方程

对任意一种连通图，我们将$2$号点连的边全部删去，还与$1$号点连通的点与$1$号点组成一个组，剩余点与$2$号点组成一个组

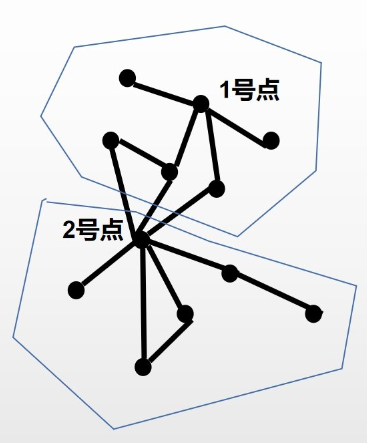
假设$1$号点所在连通块一共有$j$个点，则剩余的点有$i-j$个

不考虑这两部分的相连问题，一共有$f[j]\times f[i-j]$种图，然后考虑相连，注意只能与$2$号点相连，所以一共有$2^j-1$种方案（注意不能都不连）

然后用组合数可以得到如下公式

$$f[i]=\sum (f[j]\times C_{i-2}^{j-1}\times (2^j-1))$$

update 2024.9.12

上面的这种递推式没有什么普遍性，还是按照蓝书来做吧，容斥原理是一个很常用的做法