回文字串

回文串一般可以考虑把串倒过来思考问题

对一个给定的串，我们将其倒序，设其长度为$l$，求出原串和倒序的串的LCS，设长度为$x$，则答案为$l-x$

证明：

我们假设已经获得了最终的回文串，然后我们将这个回文串倒序，那么肯定这个回文串与这个原串是相等的

以样例为例

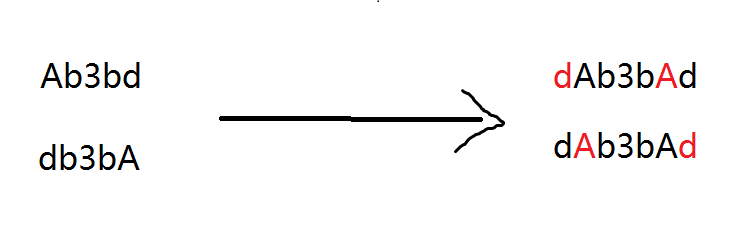
其中红色字符是添加的字符

在我们这个最终的回文串中一定不可能出现上下同一位置都为红色的情况（否则把这两个字符给去掉仍然是回文串），所以对于同一位置要么都是黑，要么一红一黑

对于一红一黑（我们只考虑上黑下红），显然就是我们添加的字符数，我们的任务就是要让这个字符数最小

对于都是黑的，就是我们最开始的串与其倒序串的LCS，这是因为LCS的长度既是上界，我们又可以构造一个方案达到这个上界

可以更严谨一点：假设输入长度为$l_1$，我们现在要做的是，指定输入的若干个字符为黑色（设为$l_0$），对于没有指定的字符（设为$l_3$），我们在输入的任意位置添加与其一模一样的字符，使得输入变成回文串

对于任意一种最终的方案，指定的红色字符个数（也就是添加的字符，与白色字符数目相等）为$l_2$，那么目标为$min{l}_2=min{l}_3=min{l}_1-l_0=l_1-max{l}_0$，有$max{l}_0$为LCS长度，证毕

这道题目还有一个做法（我自己是想到的这个做法），区间DP

设$f[i][j]$表示把区间$[i,j]$的串变成回文串所需要的最少字符

不难得出以下状态方程

这是因为对一个串来说，他的两端至少有一端是最终回文串的端点（否则可以一直删除回文串添加的新端点知道让某一端成为端点）

所以不要看到区间DP就觉得是$O(n^3)$