二维树状数组

见一本通P211

讲一下\(c_{i,j}\)表示什么，见下图

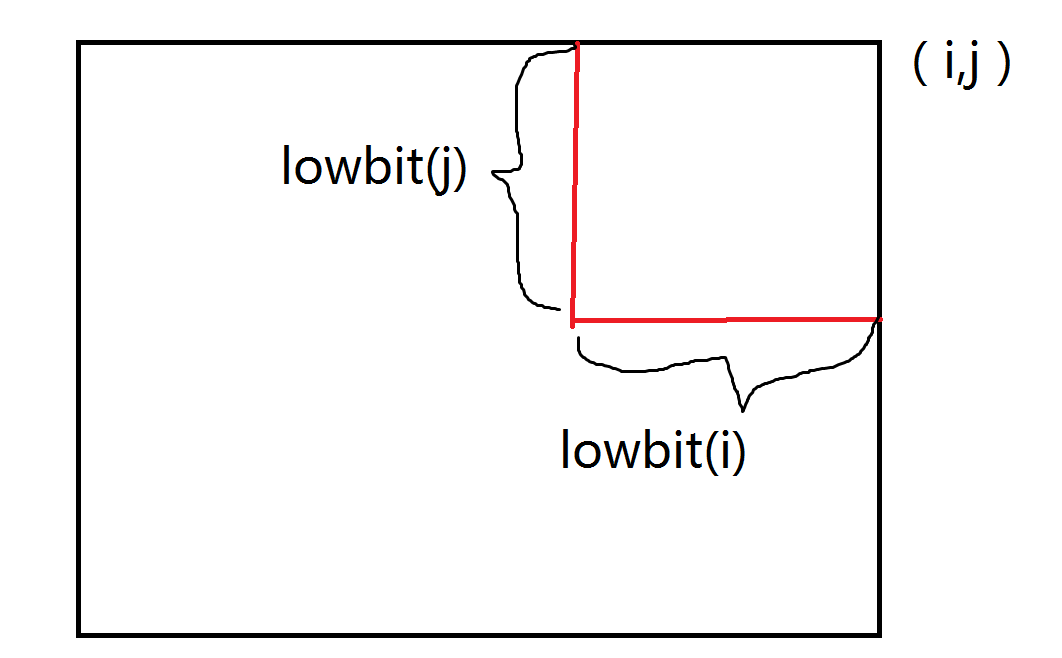
代表右上角圈起来的那一块的总和

于是再去理解书上的修改和求和代码即可

update 2024.5.13

求和是很好理解的，主要是要理解一下修改

很直观的，我们现在单点增加了，就要把所有包含这个点的矩形全部增加

设这个点是\((x,y)\)，包含这个点的矩形的右上角为\((a,b)\)，那么就有\(x∈[a-lowbit(a)+1,a]\)且\(y∈[b-lowbit(b)+1,b]\)

那么单独看每一维就是一维树状数组的找\(x\)或\(y\)的祖先的过程（即\(x+lowbit(x)=x_1,x_1+lowbit(x_1)=x_2...\)，那么\(x_i\)就是所有\(a\)的集合；\(y\)同理）

update 2024.7.28

一定要注意，两层循环里面一定要定义临时变量，别像一维树状数组这么写