12

$X=1$

首先构造题目一般都很难想到，所以我们先打上一个暴力，把序列以及模数输出

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1000;
int a[N];
int main()
{
	for(int i=1;i<=9;i++)
	{
		for(int j=1;j<=i;j++)
		a[j]=j;
		do{
			if(!check(i)) continue;
			printf("OK:");
			for(int j=1;j<=i;j++)
			printf("%d ",a[j]);
			int sum=0;
			puts("");
			for(int j=1;j<=i;j++)
			{
				sum+=a[j];
				sum%=i;
				printf("%d ",sum);
			}
			puts("");
			puts("");
		}while(next_permutation(a+1,a+i+1));
	}
    return 0;
}

输出之后可以很明显的发现两点：奇数（除了1）不可能，合法序列第一个数一定是$n$

上面的发现提示我们分奇偶讨论，对于模意义下的加法，任何一个加数加减$n$的倍数，最终结果都不变，所以我们尝试把偶数位的数字减去$n$

然后就会发现一个鹤立鸡群的数列：

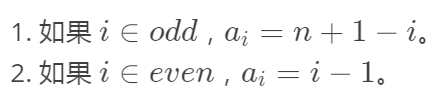
$X=2$

同理写上暴力程序

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=4e5+10;
int n;
struct Node
{
	ll x,y;
}temp[N],w[N];
int a[N];
int read()
{
    int x=0,f=1;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')f=-f;s=getchar();}
    while(s>='0'&&s<='9'){x=x*10+s-48;s=getchar();}
    return x*f;
}
bool check(int n)
{
	int sum=1;
	bool mark[20];
	memset(mark,0,sizeof(mark));
	for(int i=1;i<=n;i++)
	{
		sum*=a[i];
		sum%=n;
		if(mark[sum]) return 0;
		mark[sum]=1;
	}
	return 1;
}
int main()
{
	for(int i=1;i<=9;i++)
	{
		for(int j=1;j<=i;j++)
		a[j]=j;
		do{
			if(!check(i)) continue;
			printf("OK:");
			for(int j=1;j<=i;j++)
			printf("%d ",a[j]);
			int sum=1;
			puts("");
			for(int j=1;j<=i;j++)
			{
				sum*=a[j];
				sum%=i;
				printf("%d ",sum);
			}
			puts("");
			puts("");
		}while(next_permutation(a+1,a+i+1));
	}
    return 0;
}

这就很容易发现，除了1和4，必须要质数才可以，而且有一个模序列鹤立鸡群

1 2 3 ... n-1 0

所以我们尝试构造这个序列，就是

由于$s_{i}modn=i$，故最开始的式子可以写作

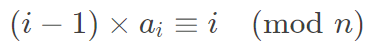
这是一个线性同余方程，我们写成$(i-1)a_i+ny=i$，当$n$是质数时就有解

通解为$x_0+kn$，显然在模$n$意义下，$a_i$是唯一的

同理我们把$i$当做未知数，写成$(a_i-1)i\equiv a_i(modn)$

同理可以得到$i$也是唯一的，所以我们在递推的过程中，不会生成相同的$a_i$，也就符合题意了

以上启发我们，如果有$b_i\equiv f(i)$，而$b_i$是由$b_{i-1}$与$a_i$（其中$a_i$是给定的序列）通过某种关系得到，就可以把$b_i$换成$f(i)$，就是把递推换成了通向，再去进行求解