【whk】高考物理:磁场
磁现象笔记
1 磁场
1.1 引入
我们回想一下,初中的时候你可能做过【通电导线】放在磁场当中会转起来,这里我们就引入两个前人发现的现象:
- 电流周围有磁场
- 通电导线再磁磁场中受力
类比电场强度(\(E=\dfrac{F}{q}\)),我们要提出一个磁场强度 \(B\),它的定义应该是由受力大小比上一个什么东西。那么既然是通电导线在磁场中的受力,对于导线,重要的物理量就是长度和所通过的电流。我们就定义 \(B=\dfrac{F}{IL}\)。
这里声明一个常见的记号:\(\cdot\) 表示垂直于纸面向外,\(\times\) 表示垂直于纸面向内。
1.2 安培定则 / 右手螺旋定则
直线电流
一图流。一定要弄清楚这个定则讲了什么:这个定则是【直线电流】周围产生的【磁感线】方向的定则。

在任何一个过导线的*面上,应该都有 \(\LARGE\cdot \uparrow^I\times_B\) 的规律。
环形电流
一图流 2.0,不过这个初中讲的。一定要弄清楚这个定则讲了什么:这个定则是【环形电流】周围产生的【磁感线】的方向的定则。

看一个切片:\(\LARGE\circlearrowleft\kern{-24px}\cdot\),\(\LARGE\circlearrowright\kern{-24px}\small\times\)。外面是环形电流的方向,里面是磁感线方向。
这里做一个补充,小磁针的 N 极指向磁感线方向。事实上,你可以把一个线圈看作一个条形磁铁,\(B\) 从 S 指向 N。
题目一般会把导线缩成一个点(或者叉)帮助你看,那么判断 \(B\) 的方向的时候,要注意和电场强度方向不一样的地方:\(B\) 的方向垂直于两点连线,至于方向比一下手就好了。
1.3 左手定则 / 安培力方向判断
如图。磁感线刺向掌心,四根手指指向电流,拇指方向是安培力方向。
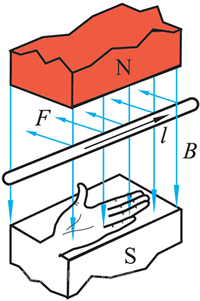
一定要注意,如果不需要判断力,一定不要拿出你的左手。使用左手定则要注意:\(F\perp B\),\(F\perp I\),但是注意 \(B\) 不一定垂直于 \(I\)。
- 注意:对于一根弯的导线,\(L\) 只看起点到终点就行。但是注意,这个长度的等下不会影响 \(R=\dfrac{\rho L}{S}\) 的计算,换句话来说,如果一个题目把两条等效之后一样长的导线并联接入电路,它们的电流是不一定相等的,相应的安培力也不一定等。
例题:

如果 \(F_{MN}=F\),则 \(F_{MLN}=0.5F\)。
1.4 电流之间的相互作用
我们考虑两条放的很*的*行导线 \(I_1\),\(I_2\),现在考虑它们方向相反。
- 那么分别考虑两条导线,对于 \(I_1\),先用右手定则判断 \(I_2\) 的 \(B\),应该是垂直于纸面向外的。再用左手定则判断 \(I_1\) 的 \(F\),大拇指向外(图上是向左),对于 \(I_2\) 应该向外(图上是向右),所以结论是相互排斥。
现在考虑他们方向相同。
- 相同的,对于 \(I_1\),先用右手定则判断 \(I_2\) 的 \(B\),应该是垂直于纸面向里的。再用左手定则判断 \(I_1\) 的 \(F\),大拇指向内(图上是向右),对于 \(I_2\) 应该向内(图上是向左),所以结论是相互吸引。
结论:同向电流相吸,异向电流相斥。
1.5 磁场导致的运动流程
例题:

这个题目答案是 \(\bm{\sf{\color{#0000ff} D}}\)。
解析:首先要分析通电导线的运动,就看条形磁铁的磁场。画出经过电流的磁感线,切线与 \(a\) 处电流成 锐角:伸出左手,显然 \(a\) 会被往外拽。与此同理:\(b\) 会往里靠。AB 错了。
转进去之后,通电导线就变成了一个 \(\otimes\),这个时候再做一个左手定则,发现力的方向向下,于是做完了,选 D。
然后这里你也要注意不要被定式思维困住了,动的不一定是通电导线,也有可能是磁铁。
1.6 洛伦兹力
洛必达力
注意对象: 洛伦兹力(\(f_{洛}=Bvq\))说的是微观层面上的力,定义是在磁场中带电粒子的受力,方向和速度垂直(洛伦兹力不做功!)。
其实,\(F_{安}=BIL=Bnesv\) 本质上就是洛伦兹力的合力。
方向判断:带正电的时候,左手定则,磁感线穿掌心,四指方向为速度方向(带正电粒子的运动方向其实就是电流方向),拇指的方向就是受力方向。负电把手指翻下去反过来就行。
例题:

这个题目答案是 \(\bm{\sf{\color{#0000ff} {AD}}}\)。
动能一样是肯定的,因为洛伦兹力不做功,做功的只有 \(mgh\),所以 A 对。因为 \(\dfrac{v^2}{L}=a_n\),所以当然 D 也对。
这个时候别被骗了,虽然 \(f_洛=Bqv\) 不假,但是显然方向不同,所以 C 是错的。
然后看最低点受力分析,不妨认为它带正电,
- 如果是向右的,\(T_1-mg-Bqv=m\dfrac{v^2}{L}\)
- 如果是向左的,\(T_2-mg+Bqv=m\dfrac{v^2}{L}\)
\(T_1\not=T_2\) 显然,B 错。
例题:在一个叉磁场中有一个竖直粗糙板,放一个带正电物体靠*板,给一个 \(v_0\) 下滑,试讨论 \(v-t\) 图像。
受力分析,\(G=mg,F_N=f_洛,f_{洛}=Bqv,f=\mu F_N\)。
我们什么都不知道,要是 \(\mu Bqv_0\le G\) 咋办?那就只能匀速直线运动了啊。
要是 \(\mu Bqv_0> G\) 则不然,显然合力向上,向下减速,但这样就会导致 \(v\) 减小,从而 \(f\) 减小,于是 \(a\) 减小,所以会做一个 \(a\downarrow v\downarrow\) 的运动,
你也许注意到了,\(v\perp F\) 如果不再受其它力,那么这个时候就会做匀速圆周运动:
- \(Bvq=m\dfrac{v^2}{r}\to r=\dfrac{mv}{qB}\)
- 当然 \(T=\dfrac{2\pi m}{qB}\) 也可以推出来,这个式子竟然和初速度没有关系,只和磁场本身和比荷有关系。这个结论可以进行记忆。
- 与此同时,要判断电荷的运动时长,就可以根据 \(\dfrac{\theta}{2\pi}T\) 判断。
应该根据匀速圆周运动的知识可以据此完成一系列题目。
例题:

如果 \(m_a=m_b=m_c\),\(q_a=q_b=q_c\) 这里力针对 \(a,b,c\) 的各个量进行对比。
如果比荷都相等,那么产生这样的差异的情况原因在于初速度不同。
- 首先 \(R=\dfrac{mv}{qB}\),这就代表说 \(v_a<v_b<v_c\)。
- 从而,\(f_洛=Bvq\) 就可以知道 \(f_{洛a}<f_{洛b}<f_{洛c}\)。
- 同时 \(T=\dfrac{2\pi m}{qB}\),\(T_a=T_b=T_c\)。
- 因为 \(\bm{\theta_c<\theta_b<\theta_a}\),所以运动时间最长的是 \(\bm a\)。

这个题目答案是 \(\bm{\sf{\color{#0000ff} {B}}}\)。
这是经典的对磁场的运用:质谱仪。
在电磁场中,带电粒子显然会受两个力 \(f_洛=Bvq\)(向上),\(F=qE\)(不知道),那么既然在竖直方向上*衡,所以\(qE=Bvq\),而且电场力方向向下。也就是 \(v=\dfrac{E}{B}\),是一个定值。因此在偏转磁场,我们是通过比荷不同来区分不同的电荷的。\(R= \dfrac{mv}{qB_2}\),半径越大,比荷越小,所以 CD 全错的。
注意到在右面的偏转磁场中的旋转方向,采用左手定则判断:粒子带正电。此时可以选出 B,但是保险起见:因为在电磁场中,粒子收到向下的电场力,所以说 \(P_2\) 带电与之相反,也就是负电。
这个题目虽然很简单,但是却是经常考察的模型。
1.(6.5) 几何关系
- 做题步骤:
i. 入射角等于出射角
- 这里说的是,从一个有界磁场的边缘以某个角度射进去一个带电粒子,(没有意外的话)它显然会转一圈(或者一个弧),然后再出来。这个出来的时候速度会和两点的连线成一个新的角,这个角度和原来射进去的角度是一样的。其实很好理解,一个弧形的轴对称性是容易证明的。
ii. 偏转角等于圆心角
- 偏转角说的是 \(v\) 的角度变化,圆心角说的是运动轨迹(那个弧)的角度。
iii. 小技巧:找圆心
- 考虑到垂线过圆心,所以如果你要找到圆心很简单,因为你有了初速度,末速度,所以对这两个速度作垂线,交点就是圆心。
- 放缩圆
注意到一个事实:当你的入射速度越大,这个圆的半径就越大,于是在速度方向已知的时候就会存在一个随着速度变大而变大的轨道圆,于是这个圆和磁场边界的交点就会有不同的情况。
于是就会存在一系列的边界情况……这不就是初中数学吗。
- 旋转圆
注意到一个事实:当你的入射速度一定的时候,这个圆的半径就固定了,于是在速度方向已知的时候 就会存在一个旋转的轨道圆,于是这个圆和磁场边界的交点就会有不同的情况。
这两个圆的动态变化可以描绘出带电粒子在磁场中的可能经过区域。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号