Tarjan 重温
upd.2025.7.12 小修部分逻辑错误/详细补充了部分文字解释。
upd.2025.7.13 大修点双/边双/有向图强连通的求法。
upd.2025.8.11 小修部分事实性错误,补充了部分没解释到位的地方。大修有向图强联通分量的求解
定义
割点:在无向图中,删去后使得连通分量数增加的点称为 割点。
割边:在无向图中,删去后使得连通分量数增加的边称为 割边,也称 桥。
点双连通图:不存在割点的无向连通图称为 点双连通图。根据割点的定义,孤立点和孤立边均为点双连通图。
边双连通图:不存在割边的无向连通图称为 边双连通图。根据割边的定义,孤立点是边双连通图,但孤立边不是。
点双连通分量:一张图的极大点双连通子图称为 点双连通分量(V-BCC),简称 点双。
边双连通分量:一张图的极大边双连通子图称为 边双连通分量(E-BCC),简称 边双。
强连通:对于有向图的两点 u,v,若它们相互可达,则称 u,v 强连通,这种性质称为 强连通性。
显然,强连通是等价关系,强连通性具有传递性。
强连通图:满足任意两点强连通的有向图称为 强连通图。它等价于图上任意点可达其它所有点。
强连通分量:有向图的极大强连通子图称为 强连通分量(Strongly Connected Component,SCC)。
DFS 树
无向图

有向图

割点
也就是考虑下某个点是割点的充要条件。
推导
因为 dfs 树有很好的性质,所以可以先按照原图进行 dfs 遍历,得到一颗 dfs 树。
记 x 的子树为 x 在 DFS 树上的子树,包含 x 本身,记作 $T(x)$。记 $T'(x) = V\backslash T(x)$,即整张图除了 $T(x)$ 以外的部分。
1.x 不为根
x 会有若干个子树 y,但是根据“子树独立性”,y 之间没有边相连。所以我们考虑单独的一个 y 即可。
即用 x 的子树判断 x 是否为割点。(下面的讨论围绕这句话展开,看懂了才不会晕)
断掉 x 点后,T(y) 内每个点根据树边连通,T'(x) 内每个点也根据树边连通
如果 T'(x) 内存在 z,T(y) 内存在 y',使得存在(y',z)这条边,那么 x 就不是割点。
可以肯定(y',z)这条边一定是非树边。考虑反证,如果是树边,那么 z=x,矛盾。
于是这启发我们定义:设 $f_x$ 表示与 x 通过 非树边 相连的所有点的时间戳的最小值。
则判 x 为割点的条件可写为 在 x 的子树内(此处指 T(y)),存在 $u$,对于任意一个 $u$ 都满足 $f_u \ge d_x$。($d_x$ 为 $x$ 的 dfs 序,即 dfn)
low 的真正含义)根据树形 DP,有(即通过树边/非树边更新):
$g_x = \min\left(\min_{y'\in \mathrm{son}(x)} g_{y'}, \min_{(x, y) \in E\land (x, y)\notin T} d_y\right)$
也就是相当于通过儿子更新 $g_x$,或者考虑直接用 $x$ 本身更新 $g_x$(这里 $\land (x, y)\notin T$ 是指 (x, y) 是非树边且不是 $x$ 连向儿子的边)。
所以在遍历到树边或非树边对 $g$ 更新即可。判断 x 为割点的条件就变成了:$g_y \ge d_x$
2.x 为根
由于没了 T'(x),且根据“子树独立性”,只需要看 x 是否有 >=2 棵子树即可。
这样才能保证是关于 T(x) 与 T'(x) 之间的连通性分讨。
结合上面树形 DP 的分析,其实 low 相当于:low[u] 应该是 u 节点通过若干条树边(但不能是父亲方向的树边)和一条反祖边能到达的最小 dfn。
代码
一些实现的细节。
1.对于上面那个树形 DP 转移的后半部分,忽略 (x,y)必须是非树边也不会错。
这样可能会多出来一些非法的边,从而对判断 $x$ 是割点有影响。因为是通过 $x$ 的儿子 $y$ 判断 $x$ 是否为割点,我们分析 $g_y$ 如何变化即可。
多出来的非法边:
1)一些连向儿子的树边(注意到上面的 dp 式子应该满足(x,y)!=T 才行,即非儿子的非树边),但是用儿子更新肯定没问题
2)一条连向父亲的树边。用父亲更新,即用 $d_x$ 更新 $g_y$,但是由于判断条件是 $g_y \ge d_x$,取了个等号,于是没影响。
但是割边在此处不能忽略(2),因为判断割边的条件是 $g_y > d_x$,又因为 g 每次更新都是取 min,所以取等后该式就永远不可能成立了,即会认为每条边都不是割边。
所以要把 回去的路 给判掉,但不能只判 fa,这样会将树边的重边也判为树边,实际上应该是非树边,所以只有正常统计非树边才能更新 low,并让判割边的条件失效。(即 low[v]>dfn[u])
解决方法是记录边的编号,并且用成对的编号(2a,2a+1),这样就能将当前边异或 1 转换成反边编号,判掉 回去的路。
2.$g_x$ 初始成 $d_x$ 显然没问题,对于割点割边都不影响判断。
#include <bits/stdc++.h>
using namespace std;
const int N=2e4+5;
int n, m, u1, v1, rt=0, dfn[N], low[N], tim=0, ans=0, cut[N];
vector<int> a[N];
void tarjan(int u)
{
int son=0;
dfn[u]=low[u]=++tim;
for (int i=0; i<a[u].size(); i++)
{
int v=a[u][i];
if (!dfn[v])
{
tarjan(v);
low[u]=min(low[u], low[v]);
if (u!=rt && low[v]>=dfn[u]) cut[u]=1;
son++;
}
else low[u]=min(low[u], dfn[v]);
}
if (u==rt && son>=2) cut[rt]=1;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i=1; i<=m; i++)
{
scanf("%d%d", &u1, &v1);
a[u1].push_back(v1);
a[v1].push_back(u1);
}
for (int i=1; i<=n; i++) if (!dfn[i]) rt=i, tarjan(rt);
for (int i=1; i<=n; i++) ans+=cut[i];
printf("%d\n", ans);
for (int i=1; i<=n; i++) if (cut[i]) printf("%d ", i);
return 0;
}
割边
同理,也就是考虑下某条边是割边的充要条件。
推导
和割点类似,割掉一条边 (u,v),其中 u 是 v 的父亲。会分成 T(v) 与 T'(v) 两部分。
只需要 T(v) 内的每个点不能到达 T'(v) 内的每个点,也就是 $g_v > d_u$。
注意此处是取大于,因为如果 T(v) 内的点能通过某条非树边到达 u,那(u,v)便不再是割边。
代码
具体见割点,有说过。
#include <bits/stdc++.h>
using namespace std;
const int N=2e4+5;
struct node
{
int v, w;
};
int n, m, u1, v1, rt=0, dfn[N], low[N], tim=0;
vector<node> a[N], ans;
bool cmp(node a, node b)
{
if (a.v!=b.v) return a.v<b.v;
return a.w<b.w;
}
void tarjan(int u, int from)
{
dfn[u]=low[u]=++tim;
for (int i=0; i<a[u].size(); i++)
{
int v=a[u][i].v, w=a[u][i].w;
if (!dfn[v])
{
tarjan(v, w);
low[u]=min(low[u], low[v]);
if (low[v]>dfn[u]) ans.push_back({min(u, v), max(u, v)});
}
else if ((w^1)!=from) low[u]=min(low[u], dfn[v]);
}
}
int main()
{
scanf("%d%d", &n, &m);
for (int i=1; i<=m; i++)
{
scanf("%d%d", &u1, &v1);
a[u1].push_back({v1, i<<1});
a[v1].push_back({u1, i<<1|1});
}
for (int i=1; i<=n; i++) if (!dfn[i]) tarjan(i, 0);
sort(ans.begin(), ans.end(), cmp);
for (int i=0; i<ans.size(); i++) printf("%d %d\n", ans[i].v, ans[i].w);
return 0;
}
有向图强联通分量
推导
考虑先按 dfs 遍历生成出 dfs 树。
在 dfs 过程中,如果遍历到 u,结果有此时一条非树边,是不是会形成环?环内每个点是不是强联通?肯定的。此时的环就是强联通图了。

但是为了保证是找出强联通分量,我们用 low 记录 u 和它子树的所有节点 经过非树边能到达的最远点,即 dfn 最小值,就容易找出强联通分量了。
在处理 low 值时,为了方便知道强联通分量包括啥,我们用栈记录途经的点即可。
这里有向图的 dfs 生成树有横叉边,子树独立性挂掉了,原因就是多了横叉边,我们 ban 掉就好。
ban 横叉边肯定是在访问非树边时考虑的,然后处理 low 等等的信息肯定是先处理了树边再处理的非树边,所以出现一条非树边 (u, v) 时,v 一定已经被访问过了。
非树边可以分横叉边,返祖边,前向边。然后就可以分情况讨论了:
1.如果 u 是通过前向边到了点 v,low[u] 被不被更新都无所谓,没有影响,不用管前向边。
2.如果 u 是通过返祖边到了点 v,low[u] 被正常更新,没有影响,不用管。
3.如果 u 是通过横叉边到了点 v。
1)如果 v 还不属于某个 SCC(此时 v 在栈内,因为 v 肯定被访问过了,且 v 不属于某个 SCC),那么此时 u 可能与 v 以及一些其余点构成 SCC,所以要用 v 的信息更新 u。
此时的边 (u, v) 可以理解为返祖边,是有用的,不能 ban 掉。如此图(当前 u=4, v=6,如果用 v 的信息更新 u, u 会被仅有当前一个点 {4} 的 SCC,事实上应该构成一个包括 {2, 3, 4, 6} 的 SCC):
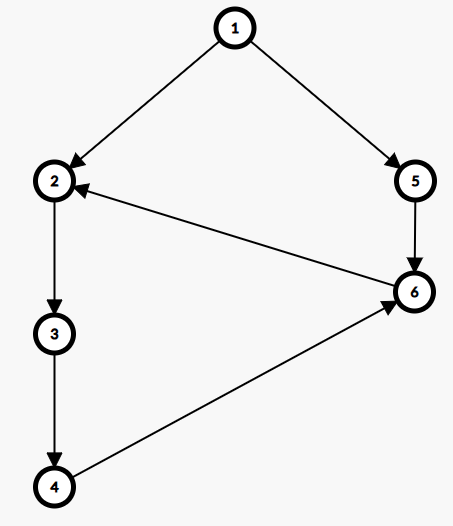
2)如果 v 属于某个 SCC(同理,此时 v 不在栈内),那么此时 u 不可能与 v 以及一些其余点构成 SCC,所以不能用 v 的信息更新 u。
也就是判下一个遍历的点 v 是否已经被加入到某个 SCC 内 或者 是否出栈 来判断是否为需要 ban 掉的横叉边。
再由 dfn 与 low 的性质:先把经过的点入栈,那么栈底到栈顶的点 dfn 严格递增,low 严格非降。
推导:对于一个连通分量图,我们很容易想到,在该连通图中有且仅有一个 u 使得 dfn[u]=low[u]。(感性理解为:相当于想尽量往上走但走不动了,这样的点有且只有一个)
该结点一定是在深度遍历的过程中,该连通分量中第一个被访问过的结点。
感谢理解为:dfn[u]=low[u] 就代表往上走不动了。反之 low[u] 还能被它的儿子更新,那么肯定可以继续往上走到一个更早访问到的节点
另外一种理解是:因为它的 dfn和 low 值最小,不会被该连通分量中的其他结点所影响。
因此,在回溯的过程中,判定 dfn[u]=low[u] 是否成立,如果成立,则栈中 u 及其上方的结点构成一个 SCC。
简述一下:
1.先复活子树独立性方便处理
2.然后发现一个重要性质,就能求有向图强联通分量了,具体如下:
这就是相当于在树上“剥叶子”,每次找到一个点 $u$,满足 $dfn_u=low_u$,那么 $u$ 所在的 SCC 一定无法往上包括更多点。
所以 $u$ 以及 $u$ 子树内的还没构成 SCC 的点会包括进一个新的 SCC。
缩点
注意到,把有向图强联通的一个部分缩成一个点,最终图一个是一个有向无环图,如果有环,那么肯定能被某个 SCC 包括。
无环往往能方便进行很多操作,比如 拓扑排序+DP(拓扑主要保证了后效性问题)
如何缩点?先求所有的 SCC,然后再根据原图的前驱后继关系,建出新图。
这样可能有重边,但是对于正常求 拓扑+DP 是没影响的。
代码
我们发现一个环内所有点的权值都可以加上,所以可以先缩点,把环内权值缩到一个点上,再 拓扑+DP。具体的,设 f[u] 表示到 u 点的最大权值。正常转移即可。
#include <bits/stdc++.h>
using namespace std;
const int N=2e4+5;
int n, m, val[N], u1, v1, rt=0, dfn[N], low[N], tim=0, cnt=0, id[N], sum[N], d[N], f[N], ans=0;
vector<int> a[N], b[N];
stack<int> stk;
queue<int> q;
void tarjan(int u)
{
stk.push(u), dfn[u]=low[u]=++tim;
for (int i=0; i<a[u].size(); i++)
{
int v=a[u][i];
if (!dfn[v])
{
tarjan(v);
low[u]=min(low[u], low[v]);
}
else if (!id[v]) low[u]=min(low[u], dfn[v]);
}
if (dfn[u]==low[u])
{
cnt++;
while (stk.top()!=u) id[stk.top()]=cnt, sum[cnt]+=val[stk.top()], stk.pop();
id[stk.top()]=cnt, sum[cnt]+=val[stk.top()], stk.pop();
}
}
void top()
{
for (int i=1; i<=cnt; i++) if (!d[i]) q.push(i), f[i]=sum[i];
while (!q.empty())
{
int u=q.front();
q.pop();
for (int i=0; i<b[u].size(); i++)
{
int v=b[u][i];
f[v]=max(f[v], f[u]+sum[v]), d[v]--;
if (!d[v]) q.push(v);
}
}
}
int main()
{
scanf("%d%d", &n, &m);
for (int i=1; i<=n; i++) scanf("%d", &val[i]);
for (int i=1; i<=m; i++)
{
scanf("%d%d", &u1, &v1);
a[u1].push_back(v1);
}
for (int i=1; i<=n; i++) if (!dfn[i]) tarjan(i);
for (int u=1; u<=n; u++)
for (int j=0; j<a[u].size(); j++)
{
int v=a[u][j];
if (id[u]!=id[v]) b[id[u]].push_back(id[v]), d[id[v]]++;
}
top();
for (int i=1; i<=cnt; i++) ans=max(ans, f[i]);
printf("%d", ans);
return 0;
}
边双
推导
注意到一点性质:一个边双一定是一个环。(因为没有割边,相当于删去某条边边双内仍然连通,那么再把被删的边加回去发现变成了环)
而找有向图强连通,也是找环。故找无向图的边双约等于找有向图的强连通。
一些不同:
1.无向图无横叉边。所以不用像求强连通那样 ban 掉横叉边(即没有 !id[v] 的判断)
2.无向图求割边不能通过来时的路返回。边双同理。
代码
#include <bits/stdc++.h>
using namespace std;
const int N=5e5+5;
struct node
{
int v, w;
};
int n, m, u1, v1, rt=0, dfn[N], low[N], tim=0, cnt;
vector<node> a[N];
vector<int> ans[N];
stack<int> stk;
void tarjan(int u, int from)
{
stk.push(u), dfn[u]=low[u]=++tim;
for (int i=0; i<a[u].size(); i++)
{
int v=a[u][i].v, w=a[u][i].w;
if (!dfn[v])
{
tarjan(v, w);
//可以顺便判割边: if (low[v]>dfn[u]) cut[w]=cut[w^1];
low[u]=min(low[u], low[v]);
}
else if ((w^1)!=from) low[u]=min(low[u], dfn[v]);
}
if (dfn[u]==low[u])
{
cnt++;
while (stk.top()!=u) ans[cnt].push_back(stk.top()), stk.pop();
ans[cnt].push_back(stk.top()), stk.pop();
}
}
int main()
{
scanf("%d%d", &n, &m);
for (int i=1; i<=m; i++)
{
scanf("%d%d", &u1, &v1);
a[u1].push_back({v1, i<<1});
a[v1].push_back({u1, i<<1|1});
}
for (int i=1; i<=n; i++) if (!dfn[i]) tarjan(i, 0);
printf("%d\n", cnt);
for (int i=1; i<=cnt; i++)
{
printf("%d ", ans[i].size());
for (int j=0; j<ans[i].size(); j++) printf("%d ", ans[i][j]);
puts("");
}
return 0;
}
点双
推导
发现一点性质:对于一个点双连通分量,它在 DFS 搜索树中 dfn 值最小的点一定是割点或者树根。
如何证明,分类讨论下。
1.当这个点为割点时,它一定是点双连通分量的根,因为一旦包含它的父节点,他仍然是割点。
2.当这个点为树根时:
a. 有两个及以上子树,它是一个割点。
b. 只有一个子树,它是一个点双连通分量的根。
c. 它没有子树,视作一个点双。
所以在遍历 (u,v) 时找发现 u 是割点(即 low[v]>=dfn[u]),那么 u 和 栈中 v 及 v 以上的点构成一个点双。
因为此时不能往 u 父亲方向扩展更多节点,那么此时一定找到了一个极大点双连通分量。
这样的过程是正确的。一种理解(可以结合下图理解):
假定 V 是 v 所属于的点双编号。
判断 u 为割点是回溯时通过 v 判断的,所以 v 子树所有点一定被访问过,且全部在 v 之后访问,也就是栈中 v 往上一直到栈顶都属于 V。
因为是递归往下处理,对于 v 子树内的其余点所构成的另一个点双的情况,在之前往下递归判割点时已经处理掉了。
这相当于每次从树上自底而上剥叶子。

需要注意的地方:Tarjan 求点双连通分量的时候,将块出栈时,只能出到 u 的孩子 v 为止。
因为 u 作为割点极有可能是该块与别块公用的,这样若是每次都出栈到 u,则会破坏其他块
正因如此,每次弹栈是弹到 u 的孩子 v,如果 u 没有任何一个 v,咋办。特判,此时 u 是一个孤立点,也算一个点双。
代码
一些细节:
1.注意判自环,图内不应该有自环,不然当有孤立点时会误判该孤立点非点双。
2.可以顺便判割点,但此处懒得再写了。
#include <bits/stdc++.h>
using namespace std;
const int N=5e5+5;
int n, m, u1, v1, dfn[N], low[N], tim=0, cnt=0;
vector<int> a[N], ans[N];
stack<int> stk;
void tarjan(int u)
{
stk.push(u), dfn[u]=low[u]=++tim;
if (a[u].size()==0)
{
ans[++cnt].push_back(u);
return ;
}
for (int i=0; i<a[u].size(); i++)
{
int v=a[u][i];
if (!dfn[v])
{
tarjan(v);
low[u]=min(low[u], low[v]);
if (low[v]>=dfn[u])
{
cnt++;
while (stk.top()!=v) ans[cnt].push_back(stk.top()), stk.pop();
ans[cnt].push_back(stk.top()), stk.pop();
ans[cnt].push_back(u);
}
}
else low[u]=min(low[u], dfn[v]);
}
}
int main()
{
scanf("%d%d", &n, &m);
for (int i=1; i<=m; i++)
{
scanf("%d%d", &u1, &v1);
if (u1==v1) continue;
a[u1].push_back(v1);
a[v1].push_back(u1);
}
for (int i=1; i<=n; i++) if (!dfn[i]) tarjan(i);
printf("%d\n", cnt);
for (int i=1; i<=cnt; i++)
{
printf("%d ", ans[i].size());
for (int j=0; j<ans[i].size(); j++) printf("%d ", ans[i][j]);
puts("");
}
return 0;
}
应用
1.有向图缩点后是一个 DAG。可以理解为若干条链组成的图
2.边双缩点后是一颗树,可以方便考虑很多树上问题
例题
水了好多题。。。比较水的题就不贴代码了。
板子类
求有向图强连通分量:B3609,P1726
求有向图点数大于 1 的强连通分量个数:P2863
求割点:UVA315
求点双:B3610
分类讨论
P5058 ,一句话题意:找两点之间的割点。
根据 dfn序 分类讨论节点位置,题解:嗅探器(割点)
一种错误方法,这里详细展开:
以 a 点跑 tarjan 处理出每个节点的 low 值,以及 dfn序 相对应的节点 p[u],然后不断去找 y 到 a 的路径上 y 必须经过的点,也就是 p[low[y]]。
此时就可以在此处安装一个嗅探器。然后继续往该必经点的必经点跳。
#include <bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int n, u1, v1, dfn[N], low[N], tim=0, x, y, p[N], ans=0;
vector<int> a[N];
void tarjan(int u)
{
dfn[u]=low[u]=++tim, p[tim]=u;
for (int i=0; i<a[u].size(); i++)
{
int v=a[u][i];
if (!dfn[v])
{
tarjan(v);
low[u]=min(low[u], low[v]);
}
else low[u]=min(low[u], dfn[v]);
}
}
int main()
{
scanf("%d", &n);
while (1)
{
scanf("%d%d", &u1, &v1);
if (u1==0 && v1==0) break;
a[u1].push_back(v1);
a[v1].push_back(u1);
}
scanf("%d%d", &x, &y);
tarjan(x);
ans=-1;
int t=p[low[y]];
if (t!=y && t!=x) ans=t;
while (low[t]!=dfn[t])
{
t=p[low[t]];
if (t!=y && t!=x) ans=min(ans, t);
}
if (ans==-1) printf("No solution");
else printf("%d", ans);
return 0;
}
这就是没有正确理解 low 含义才打出来的代码。
low 仅仅代表往下走若干条树边,再走一条返祖边。仅仅是用于判割点/割边而建立的,而不是必经点。
只有割点才是必经点,但是 low 指向的点不是必经点,只是辅助于算 割点/割边 的。
也就是对于此题。我不一定走某条返祖边到 low,我还可以走向上的父亲的树边。
hack:
in: 6 3 1 5 1 4 3 2 6 1 6 6 4 4 5 0 0 6 5 out: No solution
缩点后解决一类与连通性有关的问题
有向图:
有向图缩点后变成了DAG,就可以以较低的复杂度解决一类可达性问题。
P1407 [国家集训队] 稳定婚姻 - 洛谷(Code),此题应该是解决了两点是否在同一强联通内的问题,看这篇题解:朋友
缩点后统计度,解决一类与度数有关的问题
有向图:
P2341(Code),缩点后统计出度。但是很多 corner 注意。
P2746(Code),缩点后类比二分图贪心的想,也是用入度出度去想即可。
考虑所有入度为 0 的点顺次相连后,再连向出度为 0 的点一条边。对于出度为 0 的点同样的考虑方法。
无向图:
边双缩点后变成一颗树,用割边相连。但是缩点如何处理重边?因为是边双用割边相连,我们记录割边,然后利用记录的割边缩点即可。
P2860(Code)此题是边双缩点板子,建议看看如何处理重边。一个经典套路:无向图加 (缩点后叶子结点个数+1)/2 条边可以变成边双连通图。
为什么?可以发现最终每个点的度都为至少 2,那么只要度为 1 的点两两相连即可满足条件且最小化边数。
缩点后变成DAG,解决一类DP问题
有向图缩点后变成了DAG,就可以用拓扑+DP求解问题。
但是要注意。如果给定起点终点求问题,要先按起点 dfs 一遍,把无法到达的点删去,再建一张新图跑 拓扑序。
(因为总不能直接把起点加入再拓扑吧,也不能从起点 dfs,会被卡成 n^2,只能用拓扑 or 其他算法)
为什么不能把起点直接加入队列再拓扑?因为有些点起点不一定能到达,导致你直接加入起点后拓扑,有些点的度无法被删除成 0,最后出错
hack(SP14887):
in: 3 3 1 2 1 2 3 1 2 3 1 3 2 out: 3
P3387(Code),SP14887(Code),P3627(Code)缩点后跑 dp 处理最远距离即可。后一题还可以跑最短路。
P1073,根据题意 DP。注意一下不要少情况。题解:题解:P1073 - 洛谷专栏 (luogu.com.cn)
P10944(Code),转换题意后变成要判整张图是否为一条链,只用度来判不行,因为有重边,考虑 DP,记录最长链长度就好,看看最后是不是等于结点个数。
P2515 (Code),这题缩点后整个图会变成一颗树,此时不需要拓扑了,因为拓扑就是为了确保 DP 有正确顺序,此时直接树形 DP 就是正确顺序了,也就是树上背包。
计数类
P3469 (Code),考虑一个点如果为割点,就会分成多个连通块,然后可以在边处理割点的时候边统计答案。
就是统计答案比较麻烦,可能会有重复,于是钦定每对 (x, y) 只算 1 次贡献,而不算 (y, x) 的这对贡献,最后再 *2 把贡献补回来。
也可以是算 2 次,最后对算出的总贡献推一推式子,补/减去一些少算的/多余的贡献。
判割点会单独处理根,此题是用 dfs生成树 统计答案,不能特别处理根,因为可能有的边通过返祖边直接到根,那么根就有很多相连的 "儿子" 了,此时再算贡献就会出错。实际上根的真实儿子是第一次访问到的点。
P2272 (Code)和 P10944 比较像,发现半联通子图就是一条链,于是转换成求最长路+计数(其实这里就是最长链计数)。
杂题
参考文献
1.图论 I - 洛谷专栏(包括 从动态规划的角度理解 Tarjan 算法 - 洛谷专栏)
5.我之前的 blog(主要参考了代码)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号