朋友（强连通）

https://www.luogu.com.cn/problem/P1407

 

第1题     朋友 查看测评数据信息

我们已知 n 对男女朋友，称第 i 对朋友的男方为 B(i)，女方为 G(i)。若某男 B(i) 与某女 G(j) 曾经是同学（无论是大学，高中，亦或是幼儿园阶段，i <=j），则当某方与其朋友（即 B(i) 与 G(i) 或 B(j) 与 G(j)）感情出现问题时，他们有私奔的可能性。不妨设 B(i) 和其配偶 G(i) 感情不和，于是 B(i) 和 G(j) 旧情复燃，进而 B(j) 因被戴绿帽而感到不爽，联系上了他的初恋情人 G(k) ……一串串的分手事件像多米诺骨牌一般接踵而至。若在 B(i) 和 G(i) 离婚的前提下，这 2n 个人最终依然能够结合成 n 对情侣，那么我们称第 i对 为不安全的，否则 i 就是安全的。

给定所需信息，你的任务是判断每对是否安全。

输入格式

 

第一行为一个正整数 n，表示男女朋友的对数；

以下 n 行，每行包含两个字符串，表示这 n 对男女朋友的姓名（先女后男），由一个空格隔开；

第 n+2 行包含一个正整数 m，表示曾经相互喜欢过的情侣对数；

以下 m 行，每行包含两个字符串，表示这 m 对相互喜欢过的情侣姓名（先女后男），由一个空格隔开。

所有姓名字符串中只包含英文大小写字母，大小写敏感，长度不大于 8，保证每对关系只在输入文件中出现一次，输入文件的最后 m 行不会出现未在之前出现过的姓名，这 2n 个人的姓名各不相同，1 <=n<= 4000，0 <=m<= 20000。

 

输出格式

 

输出文件共包含 n 行，第 i 行为 `Safe`（如果第i对 是安全的）或 `Unsafe`（如果婚姻 i 是不安全的）。

 

输入/输出例子1

输入：

2

Melanie Ashley

Scarlett Charles

1

Scarlett Ashley

 

输出：

Safe

Safe

 

样例解释

无

 

题目有点绕，化简一下。画个图好理解

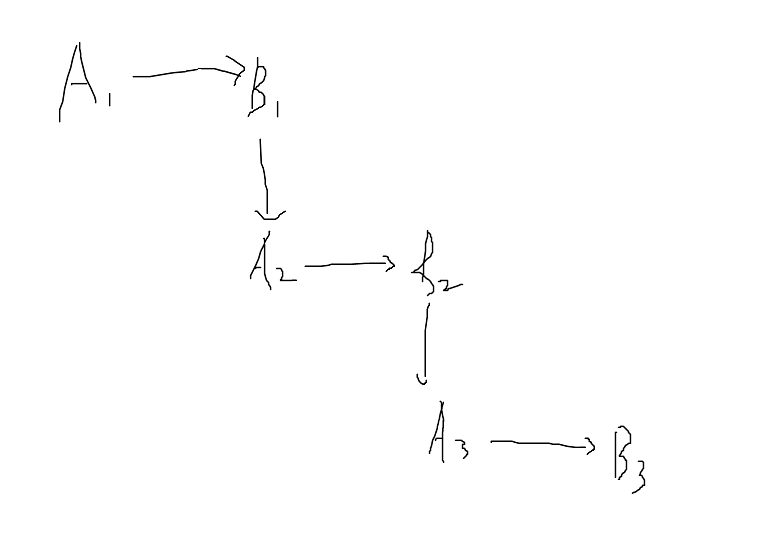
设A代表女，B代表男，根据题意，可以整理成上图所示

那么就是2个组合 {B1, A2}，{B2,A3}, 此时还有两个单身，要形成稳定婚姻，只能是 {B3,A1}。

那么可以发现此时就是一个强连通，也就是环，图中每一个点都可以到另外一个点，因为只有这样，图中的每一个人即使丢失现有配偶，也有他的配偶可选

那么我们考虑找强连通即可。

注意考虑建边的方向，如果是现在的夫妻关系，那么应该是A->B，即女到男，如果是之前的情侣关系，那么应该是B->A，即男到女，这样才能保住连通

A，B同一个强连通，不安全

不同一个， 安全

 ^{建图，特别是建边需要好好考虑，不能上来就建无向边/有向边，搞清楚点与点的关系，再去建边}

#include <bits/stdc++.h>
using namespace std;
const int N=4e4+5;

int n, m;
map<string, int> mp;
string u1, v1, g[N], b[N];
int tem=0, dfn[N], low[N], idx=0, cnt=0, id[N];
vector<int> a[N];
stack<int> st;
void dfs(int u)
{
	dfn[u]=low[u]=++idx;
	st.push(u);
	
	for (int i=0; i<a[u].size(); i++)
	{
		int v=a[u][i];
		if (!dfn[v])
		{
			dfs(v);
			low[u]=min(low[u], low[v]);
		}
		else if (!id[v]) low[u]=min(low[u], dfn[v]);
	} 
	
	if (low[u]==dfn[u])
	{
		cnt++;
		while (st.top()!=u)
		{
			id[st.top()]=cnt;
			st.pop();
		}
		id[st.top()]=cnt;
		st.pop();
	}
}
int main()
{
	scanf("%d", &n);
	for (int i=1; i<=n; i++)
	{
		cin>>u1>>v1;
		g[i]=u1, b[i]=v1;
		mp[u1]=++tem, mp[v1]=++tem; 
		
		a[mp[u1]].push_back(mp[v1]);
	}
	
	scanf("%d", &m);
	for (int i=1; i<=m; i++)
	{
		cin>>u1>>v1;
		a[mp[v1]].push_back(mp[u1]);
	}
	
	for (int i=1; i<=tem; i++)
		if (!dfn[i]) dfs(i);
	
	for (int i=1; i<=n; i++)
	{
		if (id[mp[g[i]]]==id[mp[b[i]]]) printf("Unsafe\n");
		else printf("Safe\n");
	}
	return 0;
}