嗅探器（割点）

https://www.luogu.com.cn/problem/P5058

第2题     嗅探器 查看测评数据信息

某军搞信息对抗实战演习，红军成功地侵入了蓝军的内部网络。蓝军共有两个信息中心，红军计划在某台中间服务器上安装一个嗅探器，从而能够侦听到两个信息中心互相交换的所有信息。

但是蓝军的网络相当的庞大，数据包从一个信息中心传到另一个信息中心可以不止有一条通路。

现在需要你尽快地解决这个问题，应该把嗅探器安装在哪个中间服务器上才能保证所有的数据包都能被捕获？

输入格式

 

输入文件的第一行一个整数 n，表示蓝军网络中服务器的数目。

接下来若干行是对蓝军网络的拓扑结构描述，每行是两个整数i,j表示编号为i和编号为j的两台服务器间存在双向连接。

服务器的编号从1开始，一行两个0表示网络的拓扑结构描述结束，再接下来是两个整数a,b分别表示两个中心服务器的编号。

1≤n≤2×1e5，边数不超过 5×1e5

 

输出格式

 

输出满足条件的服务器编号。如果有多个解输出编号最小的一个，如果找不到任何解，输出 No solution。

 

输入/输出例子1

输入：

5

2 1

2 5

1 4

5 3

2 3

5 1

0 0

4 2

 

输出：

1

 

样例解释

无

 

 

 

1.对于判断A，B两点的关系（是否在同一连通块），可以通过dfs序判断，（子树外/子树内/哪个节点更深等等）

2.对于求 （A,B）之间的信息，可从A点dfs，再考虑 B。这样定了一个起点（根）方便考虑问题。

3分讨是发现不够全面，要考虑以什么为标准分讨，如果发现这个标准不足以把问题分好，就再细化这个标准直到能分好。例如此题考虑一个点与B的位置关系不够，那就考虑两个点与B的位置关系。

4.割点 u 只会分离开子树 u 与非子树 u 部分。所以仅仅讨论 u 的 dfn值 是不够的。

因为这样无法讨论子树外的情况。这时引入 u 的儿子 v，再讨论需要研究的点与 v 的关系就保证正确了，因为这样保证 u 一定能分离开 v。

 

 

割点好题。

 

**题意：**无向连通图中有A、B两点，问是否存在一个点能切断A、B之间的联系。

 那这题就可以分类讨论A，B两点位置，使得A，B两点不在同一个连通块，从而找到割点

为了简化问题，我们直接从 A 点开始做DFS，找另外的B点。

 

 

最容易想到的就是判断b的时间戳（dfn）是否不小于我们找到的割点，如下图

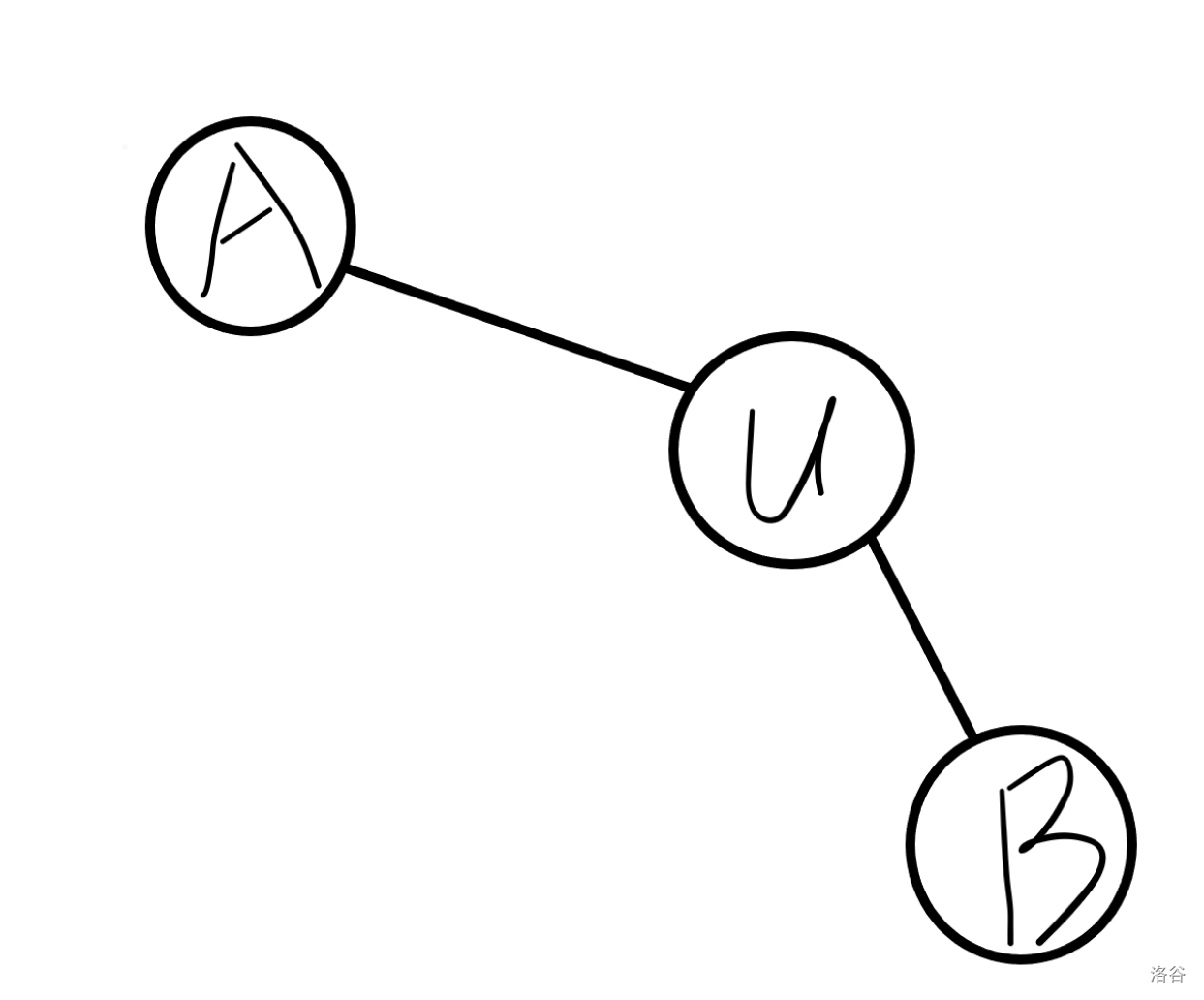
但是这种想法是有缺陷的。

假如a有一条连向b的边，但b却是由u遍历到的，那么这时u就不能分开a与b。

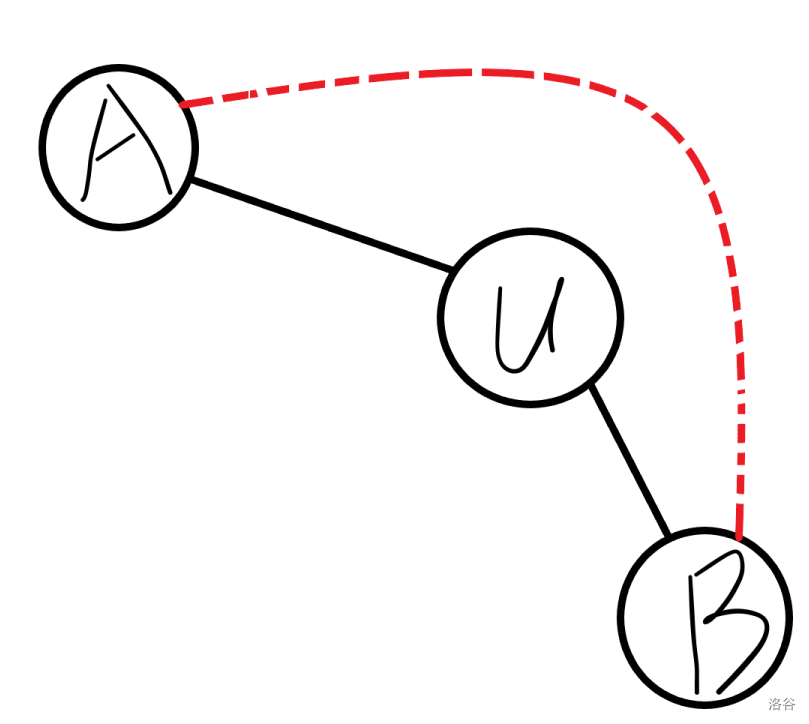
所以我们想到利用判断 u是割点的 v点，并且可以整理一下，分成三类

根据位置关系讨论，B在u点v点上方，B在u点v点之间，B在u点v点之下，这些位置关系可以用时间戳判断。

 

 

对于一个割点 u ，若判定 u 为割点的边是 (u,v),那么有以下讨论,

• 如果 dfn[b] < dfn[u]，则 b 是 u 的祖先或者 b 和 u 不在同一个子树内，由于 a 是根，那么 a 和 b一定在一个连通块内。

• 如果 dfn[b] > dfn[u] && dfn[b] <dfn[v]，则 b 是 v 的兄弟子树中的节点，无法确定 a,b 是否在一个连通块。

• 如果 dfn[b] >= dfn[v]，则 b 是 v 的子树中的节点，a,b 一定不在一个连通块。

 

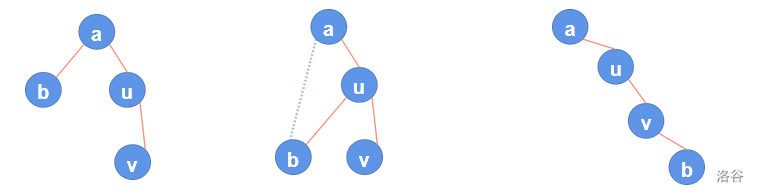
进而，我们只需要第三种情况即可。

#include <bits/stdc++.h>
using namespace std;
const int N=2e5+5;

int n, u1, v1, x, y, dfn[N], low[N], idx=0, root=0;
bool cut[N];
vector<int> a[N]; 
void dfs(int u, int fa)
{
	dfn[u]=low[u]=++idx;
	
	int child=0;
	for (int i=0; i<a[u].size(); i++)
	{
		int v=a[u][i];
		if (!dfn[v])
		{
			child++;
			dfs(v, u);
			
			low[u]=min(low[u], low[v]);
			if (low[v]>=dfn[u] && u!=root && dfn[y]>=dfn[v]) cut[u]=1;
		}
		else low[u]=min(low[u], dfn[v]);
	}
	
//	if (u==root && child>=2) cut[root]=1;
}
int main()
{
	scanf("%d", &n);
	while (scanf("%d%d", &u1, &v1) && u1 && v1)
	{
		a[u1].push_back(v1);
		a[v1].push_back(u1);
	}
	scanf("%d%d", &x, &y);
	
	root=x;
	dfs(root, 0);
	
	for (int i=1; i<=n; i++)
		if (cut[i])
		{
			printf("%d", i);
			return 0;
		}
	
	printf("No solution");
	return 0;
}