基础算法笔记
知识点
快速排序,归并排序
二分
高精度
前缀和与差分(二维)
双指针算法
位运算
离散化
区间合并
排序
快速排序
快速排序 - cn是大帅哥886 - 博客园 (cnblogs.com)
归并排序
归并排序 - cn是大帅哥886 - 博客园 (cnblogs.com)
二分
二分查找-模板 - cn是大帅哥886 - 博客园 (cnblogs.com)
高精度
高精度加减乘-模板 - cn是大帅哥886 - 博客园 (cnblogs.com)
前缀和
一维没什么说的了,主要用于求区间的一段和
S[i] = a[1] + a[2] + ... a[i]
求l,r区间和,就是 S[r] - S[l - 1],推理过程:
S[r]=a[1]+a[2]+...+a[l-1]+a[l]+...+a[r]
S[l-1]=a[1]+a[2]+...+a[l-1]
S[r]-S[l-1]=a[1]+a[2]+...+a[l-1]+a[l]+...+a[r]-(a[1]+a[2]+...+a[l-1])=a[l]+...+a[r]
二维前缀和推理过程
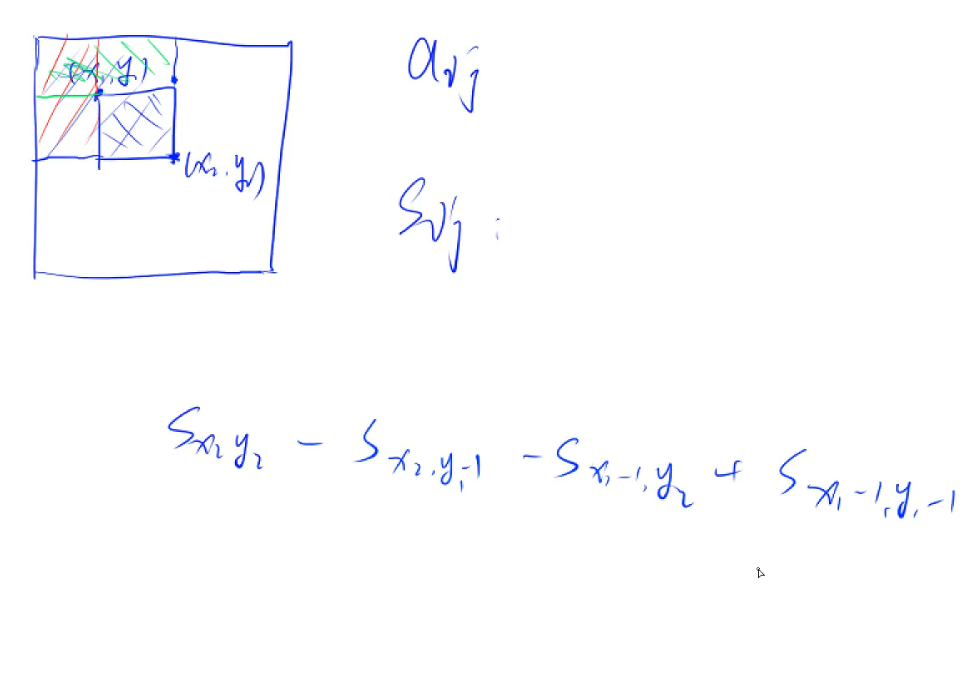
S(x,y)表示从0~x,0~y这一块矩形的和
现在要求(x1,y1)~(x2,y2)这个矩阵,可以用总矩阵s(x2,y2),减去红色面积s(x2,y1-1),减去绿色面积s(x1-1,y2),会发现有一块矩阵多减一次,加回来,就是s(x1-1,y1-1)
总结一下就是
求x1,y1,到x2,y2矩阵的和为
S(x2,y2)-S(x2,y1-1)-S(x1-1,y2)+S(x1-1, y1-1)
那么怎么初始化呢
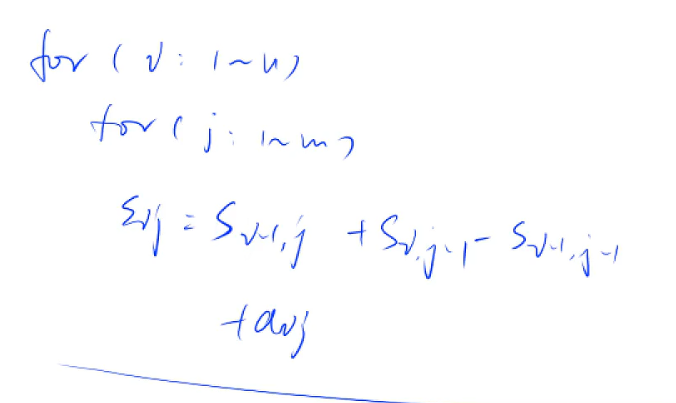

我们先求红色面积,就是S(i-1,j),橙色面积就是S(i,j-1),红色橙色重复的面积多算了,减去S(i-1,j-1),再加上本身的a(i,j)就能算出来了
总结一下
S(i,j)=S(i-1,j)+S(i,j-1)-S(i-1,j-1)+a(i,j)
总结一下:
S[i, j] = 第i行j列格子左上部分所有元素的和
以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵的和为:
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]
例题
题目描述
输入一个n行m列的整数矩阵,再输入q个询问,每个询问包含四个整数x1, y1, x2, y2,表示一个子矩阵的左上角坐标和右下角坐标。
对于每个询问输出子矩阵中所有数的和。
输入格式
第一行包含三个整数n,m,q。
接下来n行,每行包含m个整数,表示整数矩阵。
接下来q行,每行包含四个整数x1, y1, x2, y2,表示一组询问。
输出格式
共q行,每行输出一个询问的结果。
数据范围
1≤n,m≤1000,
1≤q≤200000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤矩阵内元素的值≤1000
输入样例:
3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4
输出样例:
17
27
21
#include<iostream>
using namespace std;
const int N =1010;
int a[N][N],s[N][N];
int n,m,q;
int main()
{
scanf("%d%d%d",&n,&m,&q);
for(int i=1;i<=n;++i)
for(int j=1;j<=m;++j)
scanf("%d",&a[i][j]);
//初始化前缀和
for(int i=1;i<=n;++i)
for(int j=1;j<=m;++j)
s[i][j] = s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];
while(q--)
{
int res = 0;
int x1,y1,x2,y2;
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
res = s[x2][y2] - s[x2][y1-1] - s[x1-1][y2] +s[x1-1][y1-1];
cout<<res<<endl;
}
return 0;
}
差分
ai=b1+b2+b3+...+bi
我们称a是b的前缀和,b是a的差分,要怎么构造这样的特性呢?
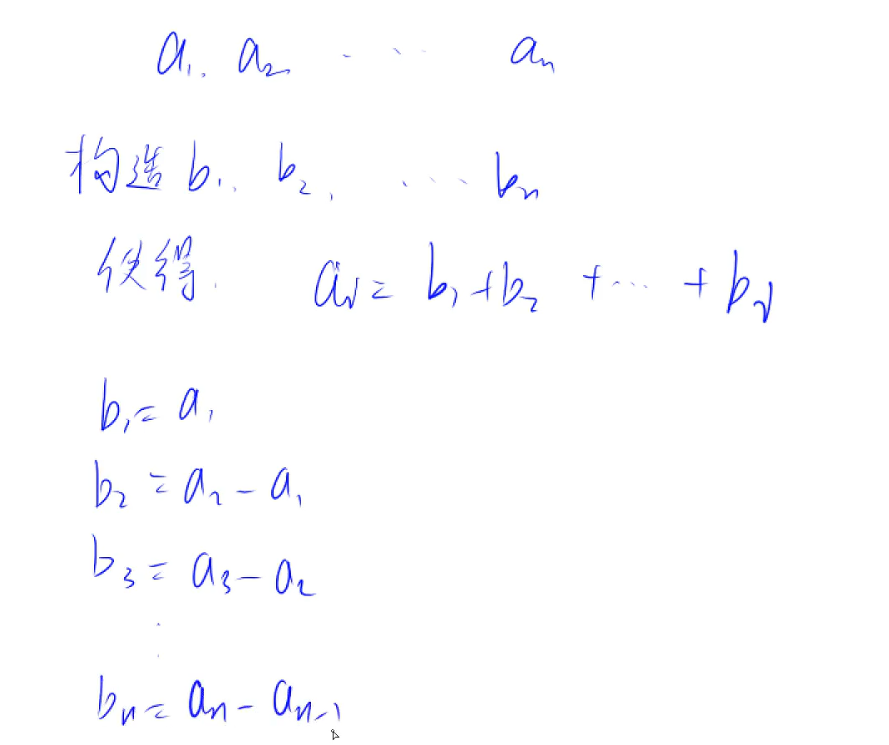
bn=an-an-1 即可,所以还发现,差分是前缀和的逆
可以发现,计算一下b数组的前缀和就可以得到a数组,这里有一个性质

[l, r]区间+c,正常是O(n)的时间的,现在
如果想要快速的让[l, r]区间+c,我们利用计算“b数组的前缀和就可以得到a数组“的特性,让bl+c,那么l~n都会+c,就是上图红色线+c,但是要求到r即可,所以br+1-c,r+1~n的数都会-c,就是绿色线的数,那么就可以做到O(1)的时间了
总结一下,就是 bl+c br-1-c
一维差分
给区间[l, r]中的每个数加上c:B[l] += c, B[r + 1] -= c
例题
797. 差分
输入一个长度为n的整数序列。
接下来输入m个操作,每个操作包含三个整数l, r, c,表示将序列中[l, r]之间的每个数加上c。
请你输出进行完所有操作后的序列。
输入格式
第一行包含两个整数n和m。
第二行包含n个整数,表示整数序列。
接下来m行,每行包含三个整数l,r,c,表示一个操作。
输出格式
共一行,包含n个整数,表示最终序列。
数据范围
1≤n,m≤1000001≤n,m≤100000,
1≤l≤r≤n1≤l≤r≤n,
−1000≤c≤1000−1000≤c≤1000,
−1000≤整数序列中元素的值≤1000−1000≤整数序列中元素的值≤1000
输入样例:
6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1
输出样例:
3 4 5 3 4 2
解题思路:
给定原数组a[1],a[2],... . ,a[N],构造差分数组b[N],使得 a[i] = b[1] + b[2] + ... + b[i],一般假定初始全部为0,用insert(i,i,a[i]) 构造出 b[N]
核心操作:将 a [ L~R ] 全部加上 C,等价于: b[L] += C , b[R+1] -= C
#include <bits/stdc++.h>
using namespace std;
const int N=100010;
int n, m, a[N], b[N]; //b是a的差分
// a数组中[l, r]区间内都加上c
void insert(int L, int R, int c)
{
b[L]+=c;
b[R+1]-=c;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i=1; i<=n; i++)
{
scanf("%d", &a[i]);
insert(i, i, a[i]); //相当于i,i这个区间加上a[i]
}
while (m--)
{
int L, R, c;
scanf("%d%d%d", &L, &R, &c);
insert(L, R, c);
}
for (int i=1; i<=n; i++)
{
b[i]+=b[i-1];
printf("%d ", b[i]);
}
return 0;
}
二维差分

要求在x1,y1到x2,y2的矩阵中全部元素+c
我们先bx1,y1+=c,把框住的右下角整个矩形+c,但是后面加多的要减回来
bx2+1 y1-=c,是绿色框-c
bx1 y2+1-=c,是红色框-c
会有一个重复区域多减了,加回来,就是
bx2+1 y2+1+=c,是红绿色框重叠+c
AcWing 798 差分矩阵
题目描述:
输入一个n行m列的整数矩阵,再输入q个操作,每个操作包含五个整数x1, y1, x2, y2, c,其中(x1, y1)和(x2, y2)表示一个子矩阵的左上角坐标和右下角坐标。
每个操作都要将选中的子矩阵中的每个元素的值加上c。
请你将进行完所有操作后的矩阵输出。
输入格式
第一行包含整数n,m,q。
接下来n行,每行包含m个整数,表示整数矩阵。
接下来q行,每行包含5个整数x1, y1, x2, y2, c,表示一个操作。
输出格式
共 n 行,每行 m 个整数,表示所有操作进行完毕后的最终矩阵。
数据范围
1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000
输入样例:
3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1
输出样例:
2 3 4 1
4 3 4 1
2 2 2 2
#include <iostream>
using namespace std;
const int maxn = 1005;
int a[maxn][maxn],b[maxn][maxn];
void insert(int x1,int y1,int x2,int y2,int c){
b[x1][y1] += c;
b[x2 + 1][y1] -= c;
b[x1][y2 + 1] -= c;
b[x2 + 1][y2 + 1] += c;
}
int main(){
int n,m,q,x1,y1,x2,y2,c;
scanf("%d%d%d",&n,&m,&q);
for(int i = 1;i <= n;i++)
for(int j = 1;j <= m;j++)
scanf("%d",&a[i][j]);
for(int i = 1;i <= n;i++)
for(int j = 1;j <= m;j++)
insert(i,j,i,j,a[i][j]); //相当于i,i到j,j的矩阵+a[i][j]
while(q--){
scanf("%d%d%d%d%d",&x1,&y1,&x2,&y2,&c);
insert(x1,y1,x2,y2,c);
}
for(int i = 1;i <= n;i++)
for(int j = 1;j <= m;j++)
a[i][j] = a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] + b[i][j]; //求前缀和
for(int i = 1;i <= n;i++){
for(int j = 1;j <= m;j++){
printf("%d ",a[i][j]);
}
printf("\n");
}
return 0;
}
双指针
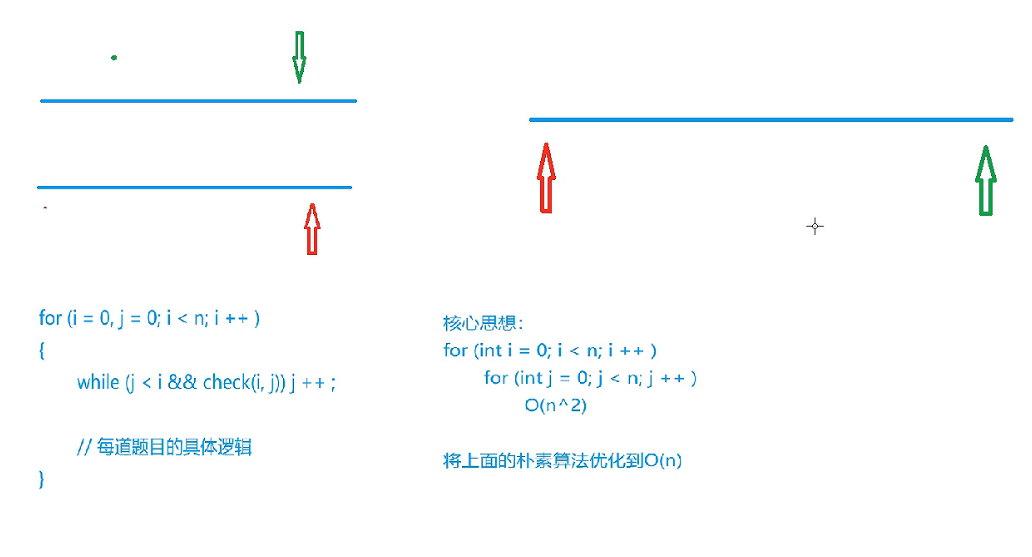
板子
for (int i = 0, j = 0; i < n; i++)
{
while (j < i && check(i, j)) j++;
// 每道题目的具体逻辑
...
}
双指针有2种
1种是2个区间,分别有指针,类似归并
1种是1哥区间,有2个指针,类似快排
左下角是模板,右下角是核心思想(优化时间的)
他做什么的呢,举个例子
比如一行字符串,要输出每个单词
输入 abc def ijk mn asfc 13
然后输出
abc
def
ijk
mn
asfc
13
这样,那么可以利用双指针解决
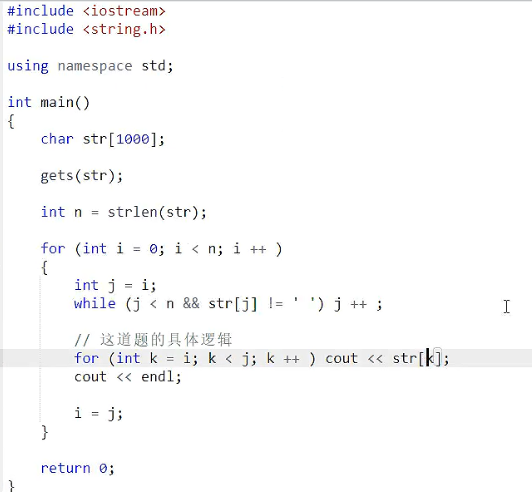
#include <bits/stdc++.h>
using namespace std;
string s;
int main()
{
getline(cin, s);
for (int i=0; i<s.size(); i++)
{
int j=i;//j的起点也要考虑一下,不一定总是0!!
while (j<=s.size() && s[j]!=' ') j++; //这里注意,条件改了,j不一定<=i,可能改的!!
for (int k=i; k<j; k++) cout<<s[k];
cout<<endl;
i=j;
}
return 0;
}
总结一下
双指针算法的核心思想就是利用了单调性质把原来通过 i, j 两重循环的O(n2)优化到O(n)。
例题:
可以看看这里:AcWing 799. 最长连续不重复子序列-CSDN博客
AcWing 799. 最长连续不重复子序列

对于双指针的题,我们要优先(最开始)就考虑一下朴素(暴力)做法,然后在想一下如何优化,题目的单调性在哪里(在这里是i和j的单调关系)
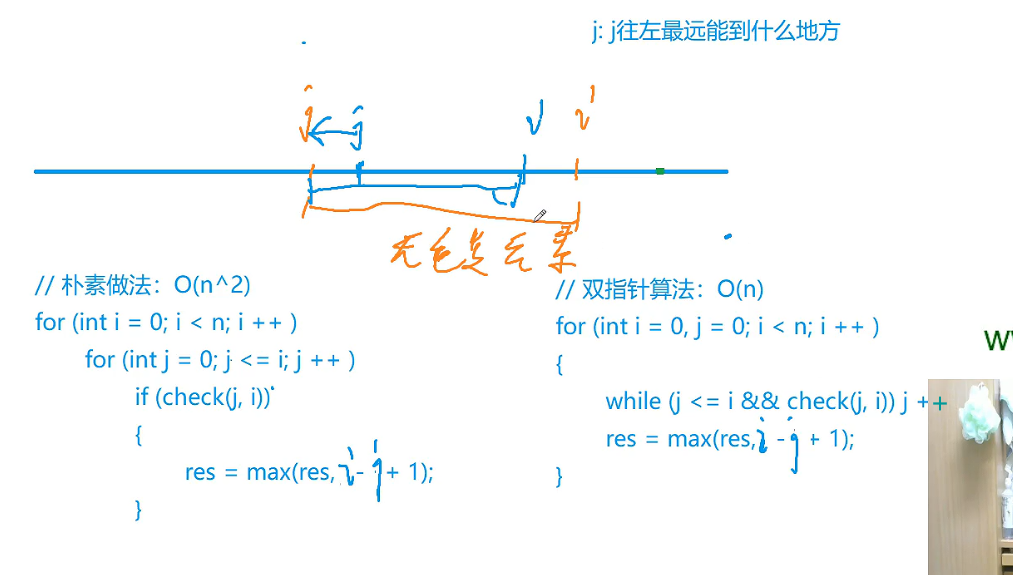
这里的j一定有单调性,因为如果i往右移动。假设j往左移动最优。那么在i往右移动前,j就本来会向左移动的(j-1,i+1区间无重复元素,那么j-1,i区间,怎么可能会有重复元素呢?但刚开始的区间是j,i,所以和j-1,i区间矛盾)
现在重点考虑一下check怎么写,因为数的范围不是很大(很大的话可以用哈希),所以用计数器s,每次i往右移,s[a[i]]++,然后判断一下这个当前的数字的数量是否大于1,如果是的话,就调整一下j
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n, a[N], s[N], j=1, ans=0;
int main()
{
scanf("%d", &n);
for (int i=1; i<=n; i++) scanf("%d", &a[i]);
for (int i=1; i<=n; i++)
{
s[a[i]]++;
while (s[a[i]]>1) s[a[j++]]--; //j如果超过i,证明区间为空,那么肯定不会有重复的数,所以不用判断 j<i
ans=max(ans, i-j+1);
}
printf("%d", ans);
return 0;
}
位运算
n的第k位是几怎么求?

简单例子,求一个十进制数的二进制数(在已知二进制位数的情况下,不过应该不用知道也可以)
输入10 4(表示n=10,二进制位数是4),输出1010
#include <bits/stdc++.h>
using namespace std;
int n, k;
int main()
{
scanf("%d%d", &n, &k);
for (int i=k-1; i>=0; i--) printf("%d", (n>>i&1));
return 0;
}
还有一个,查看二进制的反码
#include <bits/stdc++.h>
using namespace std;
int a;
unsigned int b=0;
int main()
{
cin>>a;
b=-a;
for (int i=31; i>=0; i--) printf("%d", (b>>i&1));
return 0;
}
lowbit怎么写?
x&(-x)即可,-x相当于补码,就是x按位取反然后加1

例子:AcWing 801. 二进制中1的个数-CSDN博客

#include <bits/stdc++.h>
using namespace std;
int n, a;
int lowbit(int x)
{
return x&(-x);
}
int main()
{
scanf("%d", &n);
while (n--)
{
int cnt=0;
scanf("%d", &a);
while (a) a-=lowbit(a), cnt++;
printf("%d ", cnt);
}
return 0;
}
离散化
离散化是什么?值很大,个数很少,就可以用离散化,下面举个例

可以把50000映射到4,2000映射到3......
现在知道a数组是有序的了,那么关键问题:

第一步去重有一个技巧
alls.erase(unique(alls.begin(), alls.end()), alls.end()); // 去掉重复元素
unique其实是这样的,把重复元素都放到数组的尾部,然后最后返回数组前半段没有重复的最后一个元素的下标

知道重复元素的下标后,删掉就好
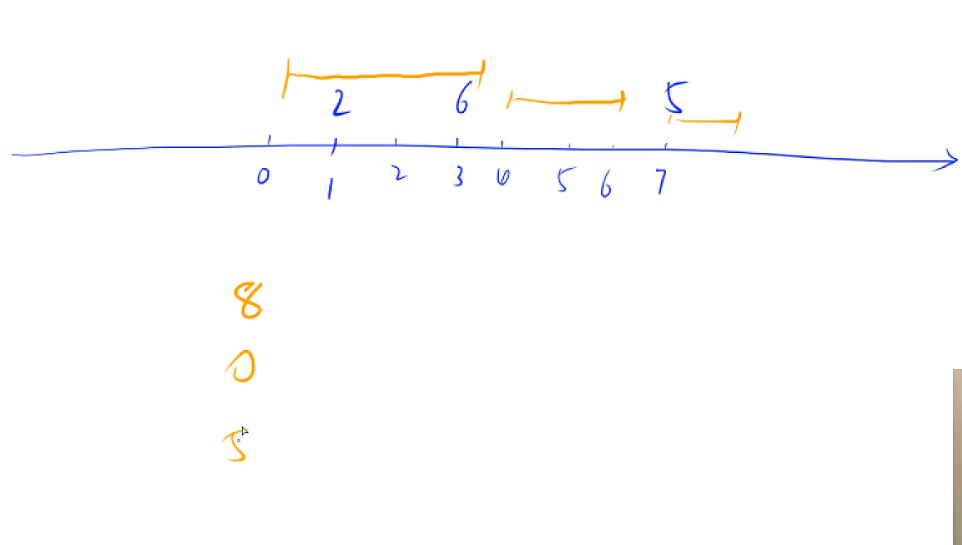
AcWing 802 区间和

3 3
1 2
3 6
7 5
1 3
4 6
7 8
输出样例:
8
0
5
样例分析
#include <bits/stdc++.h> using namespace std; const int N=3e5+5; int n, m, x[N], c[N], l[N], r[N], a[N], s[N]; vector<int> alls;
//找映射下标 int find(int x) { int L=0, R=alls.size()-1, ans=0; while (L<=R) { int mid=L+R>>1; if (alls[mid]>=x) ans=mid, R=mid-1; else L=mid+1; } return ans+1; } int main() { scanf("%d%d", &n, &m); for (int i=1; i<=n; i++) { scanf("%d%d", &x[i], &c[i]); alls.push_back(x[i]); } for (int i=1; i<=m; i++) { scanf("%d%d", &l[i], &r[i]); alls.push_back(l[i]); alls.push_back(r[i]); }
//去重 sort(alls.begin(), alls.end()); alls.erase(unique(alls.begin(), alls.end()), alls.end());
//插入 for (int i=1; i<=n; i++) { int t=find(x[i]); a[t]+=c[i]; }
//前缀和 for (int i=1; i<=alls.size(); i++) s[i]=s[i-1]+a[i];
//询问 for (int i=1; i<=m; i++) printf("%d\n", s[find(r[i])]-s[find(l[i])-1]); return 0; }
手动实现unique,类似双指针


区间合并
区间合并(超详细逐步讲解/例题/思路分析/参考代码)-CSDN博客
贪心,思路
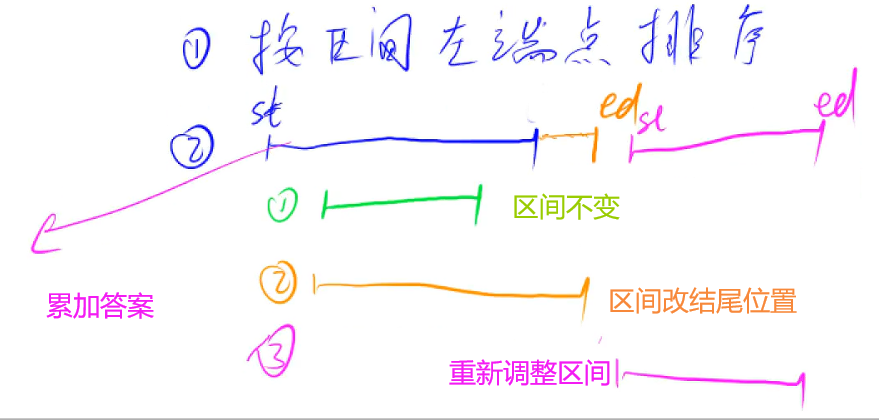
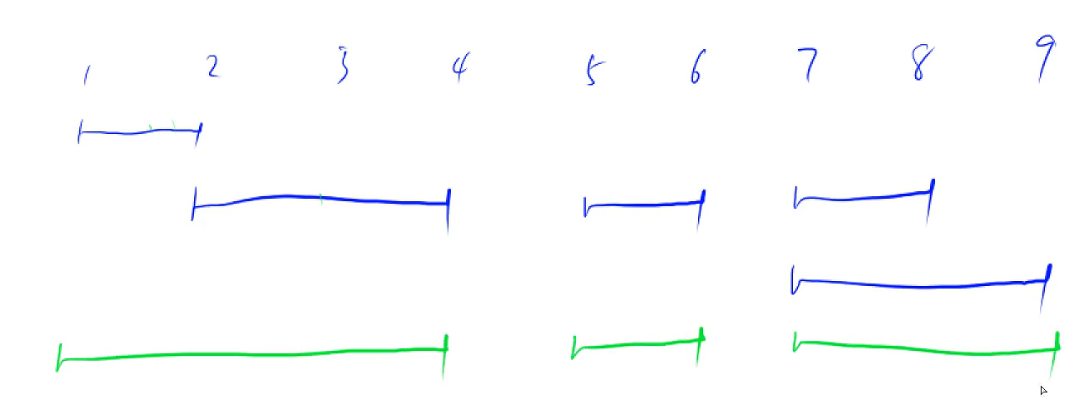
只有这3种情况,因为左端点排序了,下一个区间的左端点一定不会比当前这个区间的左端点要前
例题
AcWing 803. 区间合并
1、题目(来源于AcWing):
给定 n 个区间 [li,ri],要求合并所有有交集的区间。
注意如果在端点处相交,也算有交集。
输出合并完成后的区间个数。
例如:[1,3]和[2,6]可以合并为一个区间[1,6]。
输入格式
第一行包含整数n。
接下来n行,每行包含两个整数 l 和 r。
输出格式
共一行,包含一个整数,表示合并区间完成后的区间个数。
数据范围
1≤n≤100000,
−109≤li≤ri≤109
输入样例:
5
1 2
2 4
5 6
7 8
7 9
输出样例:
3
样例解释:
#include <bits/stdc++.h>
using namespace std;
const int N=100005;
int n;
struct node
{
int L, R;
}a[N];
bool cmp(node a, node b)
{
if (a.L==b.L) return a.R<b.R;
return a.L<b.L;
}
int merge()
{
sort(a+1, a+1+n, cmp);
int st=-2e9, ed=-2e9, cnt=0;
node res[N];
for (int i=1; i<=n; i++)
if (a[i].L>ed)
{
if (st!=-2e9) res[++cnt]={st, ed};
st=a[i].L, ed=a[i].R;
}
else if (a[i].L<=ed) ed=max(ed, a[i].R);
if (st!=-2e9) res[++cnt]={st, ed};
return cnt;
}
int main()
{
scanf("%d", &n);
for (int i=1; i<=n; i++)
scanf("%d%d", &a[i].L, &a[i].R);
printf("%d", merge());
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号