二分查找-模板

二分要注意边界

有单调性的题目一定可以用二分，但没有的话也可能可以用二分

二分的L，R端点取在哪里在于答案是否包含mid

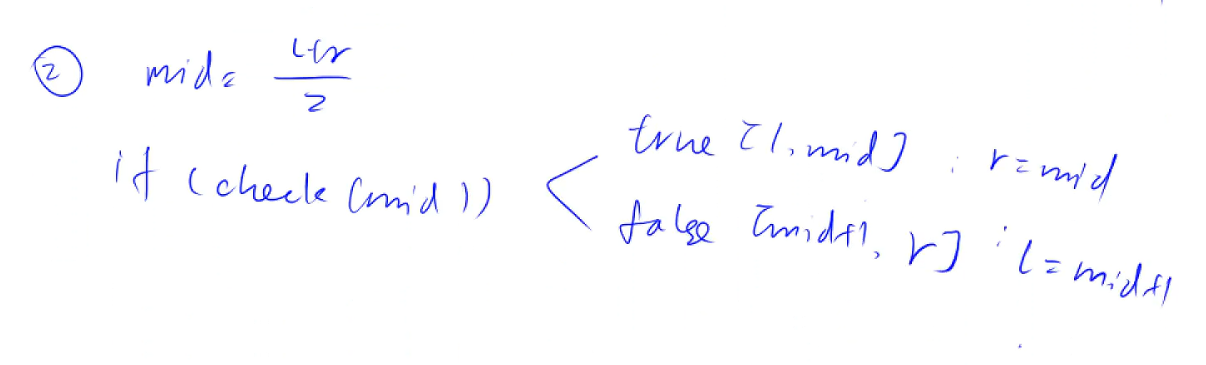
 ①中，答案在绿色线中，②中，答案在红色线中，注意，红绿色线不一定是紧挨的，他们只是情况是否满足而是

为什么mid要+1取？如果l=r-1，即r=l+1

那么mid会变成（2l+1） / 2=l，如果此时check恰好为true，那么会陷入死循环

所以分析问题可以先考虑答案在哪个区间，再接着考虑调整左右端点

 

 

 

方法1-推荐/常用

l , r
while(l <= r)
{
    m = (l + r) / 2;
    if(check())
    {
        ans = m;
        l = m + 1;
    }
    else r = m - 1;
}

　

方法2

l , r
while(l < r)
{
    m = (l + r) / 2;//左 
    if(check())
    {
        ans = m;
        r = m;
    }
    else l = m + 1;
}

　　

方法3

l , r
while(l < r)
{
    m = (l + r) / 2 + 1;//右 
    if(check())
    {
        ans = m;
        l = m;
    }
    else r = m - 1;
}

　　

 

二分查找的模板 https://www.luogu.com.cn/problem/P8814 基于此题而写 此题答案（用到二分）：

#include <bits/stdc++.h>
#define int long long
using namespace std;

int k, n, d, e;
signed main()
{
    scanf("%lld", &k);
    while (k--)
    {
        scanf("%lld%lld%lld", &n, &d, &e);

        int x=n+2-d*e;//p+q
        int L=1, R=(x>>1), mid=0, ans=0, q=0;
        while (L<=R)
        {
            mid=((L+R)>>1); //p
            q=x-mid; 
            if (q*mid<=n)
            {
                ans=mid;
                L=mid+1;
            }
            else R=mid-1;
        }
        if (ans*(x-ans)==n) printf("%lld %lld\n", ans, x-ans);
        else printf("NO\n");
    }
    return 0;
}
/*
题 
qd=n
(q-1)(d-1)+1=de

n    d   e
770  5   77
q  d
2 385

1
770 5 77

2 385

d   e
393 3
32*39=1248

n    d   e
1248 393 3
q   d
32 39
34 35

析 
n+2-de=q+d
770+2-385=q+d (387) <-----
(q-1)(d-1)=de-1
(q-1)(d-1)=384

q    d
2   385
3   384
.   ...
.   ...
.   ...
193 194
(n+2-d*e)/2  至  (770+2-385)-((n+2-d*e)/2)

*/

　　

 

 

 

浮点数二分：例子，求开平方根，sqrt（x）

少了麻烦的边界条件，直接赋值即可

#include <bits/stdc++.h>
using namespace std;

double x, L, R;
int main() 
{
	scanf("%lf", &x);
	L=0, R=x;
	while (R-L>1e-8) //精度相差极小，即可退出 可以换成 for (int i=1; i<=100; i++)，推荐while
	{
		double mid=(L+R)/2;
		if (mid*mid>=x) R=mid;
		else L=mid;
	}
	printf("%.5lf", L);
	return 0;
}