Lex和Yacc(3) 使用Yacc

上一章重点介绍了lex。本章我们将把注意力转向yacc，不过我们仍会使用lex来生成词法分析器。lex识别正则表达式，而yacc识别完整的语法。lex将输入流分割成片段（词符），然后yacc将这些片段按逻辑组合起来。

本章我们将创建一个桌面计算器：从简单的算术运算开始，逐步添加内置函数、用户变量，最后实现用户自定义函数。

语法 Grammars

Yacc 会根据你指定的语法，编写一个能够识别该语法中合法“句子”的解析器。我们在此使用的“句子”一词含义较为宽泛——对于 C 语言语法来说，这些句子就是语法上有效的 C 程序。

正如我们在第一章所见，语法是一系列规则，解析器利用这些规则来识别语法上有效的输入。例如，以下是我们将在本章稍后用于构建计算器的一个语法版本：

statement → NAME = expression
expression → NUMBER + NUMBER | NUMBER − NUMBER

竖线 "|" 表示同一个符号存在两种可能性。例如，一个表达式既可以是一个加法，也可以是一个减法。箭头 "→" 左侧的符号称为规则的左部（Left-Hand Side，LHS），右侧的符号称为右部（Right-Hand Side，RHS）。多个规则可以拥有相同的左部；竖线只是这种情况的简写形式。

实际出现在输入中并由词法分析器（lexer）返回的符号称为终结符（Terminal Symbols / Tokens）；而出现在某些规则左部的符号则称为非终结符（Non-terminal Symbols / Non-terminals）。终结符和非终结符必须严格区分，将词符（Token） 写在规则的左侧是一种语法错误。

程序可能在语法上有效，但在语义上无效。例如，一个 C 程序将字符串赋值给 int 类型的变量。Yacc 只负责处理语法问题；其他验证工作取决于你。

通常表示一个已解析句子的方式是使用树形结构。例如，如果我们用这个语法解析输入 "fred = 12 + 13"，其树形结构将如图 3-1 所示。其中 "12 + 13" 是一个表达式（expression），而 "fred = expression" 则是一个语句（statement）。尽管 yacc 解析器本身不会在内存中实际创建这样的树形数据结构，但你可以自己轻松实现这一点。

graph TD A(Statement) --> G[Name fred] A --> B[=] A --> C(expression) C --> D[Number 12] C--> Plus["十"] C --> F[Number 13]

每个语法都包含一个起始符号（Start Symbol），它必须位于解析树（Parse Tree） 的根节点。在这个语法中，statement（语句） 就是起始符号。

递归的语法规则 Recursive Rules

规则可以直接或间接地引用自身。这种重要的能力使得解析任意长的输入序列成为可能。让我们扩展一下语法，使其能够处理更长的算术表达式：

expression → NUMBER
| expression + NUMBER
| expression − NUMBER

现在，我们可以通过反复应用表达式规则，来解析像 "fred = 14 + 23 − 11 + 7" 这样的序列，如图 3-2 所示。Yacc 能够非常高效地解析递归规则，因此在我们使用的几乎所有语法中，都会看到递归规则。

移进-归约分析 Shift/Reduce Parsing

Yacc 解析器的工作原理是寻找可能匹配已识别记号（Token） 的规则。当 Yacc 处理一个解析器时，它会创建一组状态（States），每个状态都反映了一个或多个部分解析规则（Partially Parsed Rules） 中的可能位置。

当解析器读取记号时，每当读到一个未完成某个规则的记号，它就会将该记号压入一个内部分析栈（Parse Stack），并切换到一个反映刚刚读取记号的新状态。这个动作称为移进（Shift）。

当它找到了构成某个规则右部（Right-Hand Side, RHS） 的所有符号时，它会将右部符号从分析栈中弹出，将该规则的左部（Left-Hand Side, LHS） 符号压入栈，并切换到一个反映栈顶新符号的新状态。这个动作称为归约（Reduce），因为它通常会减少栈上的项目数量（并非总是如此，因为可能存在右部为空的空规则（ε-production））。

每当 Yacc 归约一个规则时，它就会执行与该规则关联的用户代码（User Code） 或语义动作（Semantic Action）。这就是你实际处理解析器所解析内容的方式。

让我们看看它是如何使用图 3-1 中的简单规则来解析输入 "fred = 12 + 13" 的。

解析器首先将记号（Tokens） 逐一移进（Shift） 到内部分析栈（Parse Stack） 上：

fred
fred =
fred = 12
fred = 12 +
fred = 12 + 13

此时，它可以归约（Reduce） 规则 "expression → NUMBER + NUMBER"。于是它将数字 12、加号和数字 13 从分析栈（Parse Stack）中弹出，并用一个表达式（expression）符号替换它们：fred = expression

接着，它归约（Reduce） 规则 "statement → NAME = expression"。于是它将 fred、= 和 expression 从栈中弹出，并用一个 语句（statement） 符号替换它们。

至此，我们已到达输入末尾，并且分析栈已被归约至开始符号（Start Symbol），这表明该输入根据此文法（Grammar） 是有效的。

Yacc不能解析什么 What Yacc Cannot Parse

尽管 Yacc 的解析技术具有通用性，但有些语法（Grammar） 是 Yacc 无法处理的。

它无法处理歧义语法（Ambiguous Grammar），即同一段输入可以匹配多棵不同语法分析树（Parse Tree） 的语法。

它也无法处理那些需要向前查看（Lookahead） 多于一个记号（Token） 才能决定是否匹配了某条规则的语法。请看下面这个非常刻意的例子：

phrase       : cart_animal AND CART
             | work_animal AND PLOW

cart_animal  : HORSE
             | GOAT

work_animal  : HORSE
             | OX

这个语法不是歧义的，因为任何有效输入都只对应一棵可能的语法分析树。但是 Yacc 仍然无法处理它，因为它需要向前查看两个符号（Two-Symbol Lookahead）。

具体来说，当解析输入 "HORSE AND CART" 时，在看到 CART 之前，Yacc 无法判断 HORSE 到底是 cart_animal 还是 work_animal，而 Yacc 的向前查看能力（Lookahead） 不足以看到那么远。

如果我们把第一条规则改成这样：

phrase       : cart_animal CART
             | work_animal PLOW

Yacc 就能轻松处理了，因为它只需向前查看一个记号（One-Token Lookahead） 就能判断：当输入 HORSE 后面跟着 CART 时，这匹马就是 cart_animal；如果后面跟着 PLOW，那它就是 work_animal。

在实际应用中，这些规则并不像看起来那么复杂和令人困惑。

一个原因是，Yacc 非常清楚自己能解析哪些语法，不能解析哪些语法。如果你给它一个它无法处理的语法，它会明确告诉你，因此不存在“过于复杂的解析器静默失败”的问题。

另一个原因是，Yacc 能够处理的语法，与人们实际编写的语法高度吻合。很多时候，一个让 Yacc 困惑的语法结构，同样也会让人感到困惑。因此，如果你在语言设计上有一定的自由度，就应该考虑修改语言规范，使其既能让 Yacc 更容易解析，也能让用户更容易理解。

关于移进-归约解析（Shift/Reduce Parsing） 的更多信息，请参阅第 8 章。

若要了解 Yacc 如何将你的语法规范转换为可工作的 C 程序，请参考 Aho、Sethi 和 Ullman 的经典编译器著作《Compilers: Principles, Techniques, and Tools》（Addison-Wesley，1986 年）。该书常因其封面插图而被称为 “龙书”（Dragon Book）。

Yacc语法解析器 A Yacc Parser

一个 Yacc 语法文件与 Lex 规范文件具有相同的三部分结构（事实上，Lex 的结构借鉴自 Yacc）。

第一部分：定义部分（Definition Section）
处理对 Yacc 生成的解析器（下文简称“解析器”）的控制信息，并通常设置解析器运行所需的执行环境。

第二部分：规则部分（Rules Section）
包含解析器的语法规则。

第三部分：代码部分（C Code Section）
是 C 语言代码，会被原封不动地复制到生成的 C 程序中。

我们首先为图 3-1 中最简单的语法编写解析器，然后再逐步扩展它，使其更加实用和符合真实场景。

定义部分

定义部分包含以下内容的声明：

语法中使用的记号（Tokens）
解析器栈上使用的值类型（Value Types）
以及其他零散设置

它还可以包含一个字面代码块（Literal Block），即用 %{ 和 %} 包围的 C 代码。

我们首先通过声明两个符号记号（Symbolic Tokens） 来开始编写第一个解析器。

%token NAME NUMBER

你可以直接使用单引号字符作为记号，而无需事先声明它们。因此，我们不需要特别声明 '='、'+' 或 '-'。

规则部分

规则部分基本上就是我们前面使用的那种格式的语法规则列表。由于 ASCII 键盘上没有 → 键，我们用冒号（:）来表示规则的左部和右部，并在每条规则末尾加上一个分号（;）：

%token NAME NUMBER
%%
statement: NAME '=' expression
         | expression
         ;

expression: NUMBER '+' NUMBER
          | NUMBER '-' NUMBER
          ;

和 Lex 不同，Yacc 在语法规则部分完全不在意换行和空格。实际上，多加一些空白反而会让语法规则更容易阅读。

我们给解析器加了一条新规则：一个语句既可以是一个赋值表达式，也可以是一个普通的表达式。如果用户输入的是普通表达式，我们就会把它的计算结果打印出来。

在语法规则里，第一条规则中冒号左边的那个符号，默认就是整个语法解析的起始符号。当然，你也可以在定义部分用 %start 声明来指定一个不同的起始符号。

符号值与动作 Symbol Values and Actions

好的，已采纳您的建议。在编程和解析器语境中，将 Action 译为 “操作” 确实更自然、更准确。以下是修正后的翻译：

符号值与操作（Symbol Values and Actions）

Yacc 解析器中的每个符号（Symbol） 都有一个对应的值（Value）。这个值提供了关于该符号特定实例的额外信息。

如果一个符号代表一个数字（Number），它的值就是那个具体的数值。
如果它代表一个文本字面量（Literal Text String），它的值可能是一个指向该字符串副本的指针。
如果它代表程序中的一个变量（Variable），它的值可能是一个指向描述该变量的符号表条目（Symbol Table Entry） 的指针。
有些记号（Tokens）（例如代表右括号 ')' 的记号）则没有有用的值，因为一个右括号和另一个是一样的。

非终结符（Non-terminal Symbols） 可以拥有由您在解析器中编写的代码所定义的任何值。

通常，当一条语法规则被匹配时，其对应的操作（Action）（即花括号 {} 中的代码）会被执行。这些操作代码经常用于构建与输入对应的语法分析树（Parse Tree）。这样一来，后续的处理代码就可以一次性处理整个语句，甚至整个程序。

在我们当前构建的解析器中：

一个 NUMBER 或一个 expression 的值，就是该数字或表达式的数值。
一个 NAME 的值将是一个指向符号表（Symbol Table） 的指针。

在实际的解析器中，不同符号的值会使用不同的数据类型（Data Types）。

例如：

数值类符号可能使用 int 或 double
字符串类符号可能使用 char *
更高级的符号（如结构体）则使用指向相应结构的指针

如果你的解析器中使用了多种值类型，你必须在定义部分列出所有用到的类型。这样，Yacc 才能生成一个名为 YYSTYPE 的 C 语言 union 类型定义来容纳它们。

（幸运的是，Yacc 提供了很多机制来帮助你确保为每个符号使用正确的值类型。）

在我们计算器的第一个版本中，唯一需要关注的值就是输入数字和计算结果的数值。 Yacc 默认将所有符号的值类型设为 int，这对我们计算器的第一个版本来说已经足够了。

明白了，在您当前翻译的上下文中，将 Action 译为 “行为” 更贴切。

每当解析器归约（Reduce） 一条规则时，都会执行该规则对应的用户C代码，也就是规则的行为（Action）。

行为代码直接写在规则末尾的花括号 {} 里（在分号或竖线之前）。

在这段代码中：

可以通过 $1、$2 等引用冒号右边（Right-Hand Side, RHS） 各个符号的值。
可以通过给 $$ 赋值，来设置冒号左边（Left-Hand Side, LHS） 那个符号的值。

在我们这个解析器里，expression 符号的值就是它对应表达式的计算结果。我们添加一些代码来计算并打印表达式，这样就得到了图3-2中使用的完整语法。

%token NAME NUMBER
%%

statement: NAME '=' expression
         | expression { printf("= %d\n", $1); }
         ;

expression: expression '+' NUMBER { $$ = $1 + $3; }
          | expression '−' NUMBER { $$ = $1 - $3; }
          | NUMBER                { $$ = $1; }
          ;

构建表达式（expression）的那些规则（Rules） 负责计算相应的值，而将表达式识别为语句（Statement） 的那条规则则负责打印结果。

在构建表达式的规则中（例如 expression '+' NUMBER）：

第一个子表达式（或数字）的值是 $1。
第二个数字（NUMBER）的值是 $3。
运算符（'+' 或 '-'）的值会是 $2，不过在当前语法中，运算符本身并没有携带实际意义的值。

最后一条规则（expression: NUMBER）的行为（Action）（即 { $$ = $1; }）从严格意义上讲并非必需。因为 Yacc 在每次归约（Reduce） 之后、执行任何显式行为代码之前，会执行一个默认操作：自动将 $1 的值赋给 $$。

词法分析器（The Lexer）

为了测试我们的解析器（Parser），我们需要一个词法分析器（Lexer） 来为它提供记号（Tokens）。

正如第一章提到的，解析器是更高层的例程。每当它需要从输入中获取一个记号时，就会调用词法分析器的函数 yylex()。

一旦词法分析器找到了一个解析器感兴趣的记号，它会立即返回到解析器，并将该记号的编码（Token Code） 作为返回值。

为了使词法分析器能使用这些记号名称，Yacc 会在生成的 y.tab.h 文件（在 MS-DOS 系统上可能是类似的名字）中，将语法里定义的记号名称（如 NAME, NUMBER）定义为 C 语言的预处理器宏（C Preprocessor Macros）。这样，Lex 生成的词法分析器代码就可以通过 #include "y.tab.h" 来引用它们。

以下是一个为我们的解析器提供记号的简单词法分析器（Lexer）代码：

%{
#include "y.tab.h"   /* 包含Yacc生成的记号定义 */
extern int yylval;   /* 声明外部变量，用于向解析器传递记号值 */
%}

%%
[0-9]+        { 
                 yylval = atoi(yytext);  /* 将数字字符串转换为整数值 */
                 return NUMBER;          /* 返回记号类型 NUMBER */
              }

[ \t]         ; /* 忽略空格和制表符 */

\n            return 0; /* 换行符表示逻辑上的输入结束（EOF） */

.             return yytext[0]; /* 其他任何单个字符（如 '+', '-', '=' ）直接返回其ASCII值 */
%%

数字字符串被识别为数字（Numbers），空白字符被忽略，而换行符会返回一个输入结束记号（End-of-Input Token）（值为零），以此告知解析器没有更多内容可读。

词法分析器中的最后一条规则是一种非常常见的兜底规则（Catch-all Rule）。它的作用是：将任何其他未被前面规则处理的单个字符，都作为一个单字符记号（Single-Character Token） 返回给解析器。

单字符记号通常是标点符号，例如括号、分号，以及单字符的运算符（如 +、-、*、=）。如果解析器收到了一个它不认识的记号，它就会产生一个语法错误（Syntax Error）。因此，这条兜底规则让你能够轻松处理所有的单字符记号，同时又能借助 Yacc 的错误检查机制来捕获并报告无效的输入。

每当词法分析器向解析器返回一个记号（Token） 时，如果该记号有关联的值（Value），词法分析器必须在返回之前将这个值存储到变量 yylval 中。在这个最初的示例中，我们显式地声明了 yylval。在更复杂的解析器中，Yacc 会将 yylval 定义为一个 union（联合体）类型，并将该定义放在 y.tab.h 头文件里。我们目前还没有定义 NAME 记号，只定义了 NUMBER 记号，但这暂时没问题。

编译并运行一个简单的解析器

在 UNIX 系统上：

Yacc 会读取你的语法文件，并生成：
- y.tab.c：C 语言解析器源码。
- y.tab.h：包含记号编号（Token Number） 定义的头文件。
Lex 会读取你的词法规范文件，并生成：
- lex.yy.c：C 语言词法分析器源码。

你只需要将它们与 Yacc 和 Lex 的库（Libraries） 一起编译即可。这些库提供了所有支持例程（包括一个主函数 main()）的可用默认版本。该 main() 函数会调用解析器的入口函数 yyparse()，并在解析完成后退出。

% yacc -d ch3-01.y # makes y.tab.c and "y.tab.h
% lex ch3-01.l # makes lex.yy.c
% cc -o ch3-01 y.tab.c lex.yy.c -ly -ll # compile and link C files
% ch3-01
99 + 12
= 111
% ch3-01
2 + 3−14+33
= 24
% ch3-01
100 + −50
syntax error

我们第一个版本的计算器看起来可以正常工作了。在第三个测试用例中，当我们输入不符合语法规则的内容时，它能正确地报告一个语法错误。

算术表达式与歧义 Arithmetic Expressions and Ambiguity

现在让我们使算术表达式变得更通用和实用。我们将扩展表达式规则，以支持乘法和除法、一元负号以及括号表达式：

expression: expression '+' expression { $$ = $1 + $3; }
          | expression '-' expression { $$ = $1 - $3; }
          | expression '*' expression { $$ = $1 * $3; }
          | expression '/' expression
            {
              if ($3 == 0)
                yyerror("divide by zero");  /* 处理除零错误 */
              else
                $$ = $1 / $3;
            }
          | '-' expression { $$ = -$2; }     /* 一元负号 */
          | '(' expression ')' { $$ = $2; }  /* 括号 */
          | NUMBER { $$ = $1; }              /* 基础数字 */
          ;

除法对应的行为（Action） 中加入了除零检查，因为在许多 C 语言的实现中，除以零会导致程序崩溃。它调用了 yyerror() 这个 Yacc 的标准错误处理例程来报告错误。

但这个语法存在一个问题：它具有严重的歧义性（Extremely Ambiguous）。

例如：

输入 2+3*4 可能被理解为 (2+3)*4，也可能被理解为 2+(3*4)。
输入 3−4−5−6 可能被解释为 3−(4−(5−6))，或 (3−4)−(5−6)，或者其他多种可能的组合。

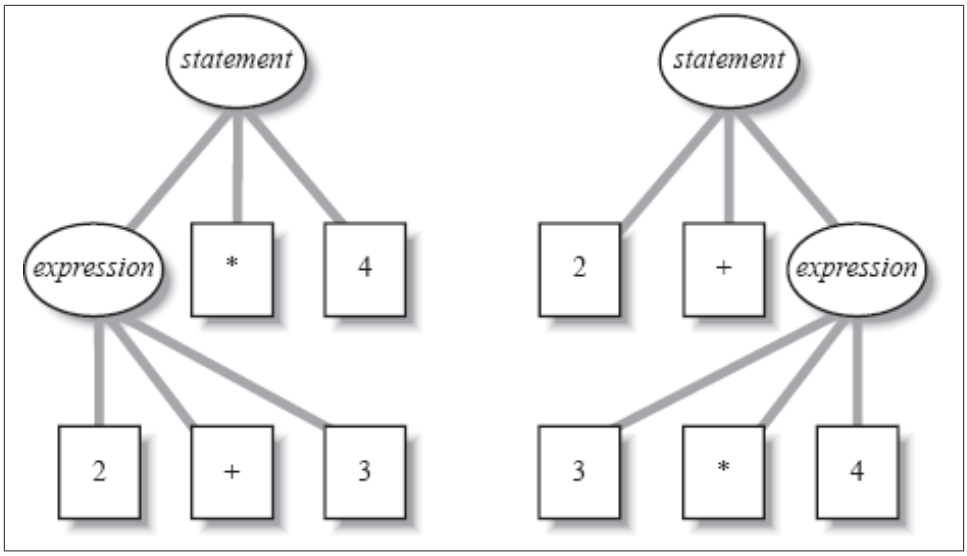
图 3-3 展示了 2+3*4 的两种可能的语法分析树（Parse Tree）。

如果你直接编译这个语法，Yacc 会提示存在 16 个移进-归约冲突（Shift/Reduce Conflicts）。这意味着解析器在多个状态中无法确定应该先将下一个记号移进（Shift） 到栈中，还是先对栈顶的符号进行归约（Reduce）。

例如，在解析 "2+3*4" 时，解析器会经历以下步骤（这里我们将 expression 简写为 E）：

2        # 移进 NUMBER 2
E        # 归约：NUMBER → E
E +      # 移进 '+'
E + 3    # 移进 NUMBER 3
E + E    # 归约：NUMBER → E

此时，解析器看到了 "*"，它面临两个选择：

立即归约：使用规则 expression: expression '+' expression 将 2+3 归约为一个表达式 E。
继续移进：将 "*" 移进栈中，期望稍后能够使用规则 expression: expression '*' expression 进行归约。

问题的根源在于，我们没有告诉 Yacc 这些运算符的优先级和结合性。

优先级（Precedence） 决定了表达式中哪些运算符先执行。数学和编程的传统（可以追溯到 1956 年第一个 Fortran 编译器）规定：乘法和除法的优先级高于加法和减法。
- 因此，a+b*c 表示 a+(b*c)。
- d/e−f 表示 (d/e)−f。

在任何表达式语法中，运算符都会被分成不同的优先级层次（Levels of Precedence），从最低到最高。总层数取决于具体的编程语言。C 语言以其过多的优先级层次而“闻名”，总共有 15 个级别。

结合性（Associativity） 控制着相同优先级运算符的分组方式。

左结合（Left Associativity）：运算符从左边开始分组。
例如，在 C 语言中 a - b - c 表示 (a - b) - c。
右结合（Right Associativity）：运算符从右边开始分组。
例如，在 C 语言中 a = b = c 表示 a = (b = c)。

在某些情况下，运算符根本不结合（Non-associative），即不允许连续使用。
例如，在 Fortran 语言中，A .LE. B .LE. C 是无效的表达式。

在语法中有两种方式来指定优先级和结合性：隐式和显式。

隐式方法：通过为每个优先级层次使用不同的非终结符来重写语法。假设所有运算符都采用通常的优先级和左结合性，我们可以这样重写表达式规则：

expression: expression '+' mulexp
          | expression '-' mulexp
          | mulexp
          ;

mulexp: mulexp '*' primary
      | mulexp '/' primary
      | primary
      ;

primary: '(' expression ')'
       | '-' primary
       | NUMBER
       ;

这是一种非常合理的语法编写方式。事实上，如果 Yacc 没有提供显式的优先级规则，这将是唯一的方法。

但是 Yacc 也允许你显式地指定优先级。我们可以在定义部分添加以下几行声明（最终语法如示例 3-1 所示）：

%left '+' '-'       /* 左结合，优先级最低 */
%left '*' '/'       /* 左结合，优先级更高 */
%nonassoc UMINUS    /* 无结合性，优先级最高（UMINUS 是代表一元负号的伪记号） */

每一行声明都定义了一个优先级层次。它们告诉 Yacc：

+ 和 - 是左结合的，并且处于最低的优先级层次。
* 和 / 也是左结合的，但处于更高的优先级层次。
UMINUS（一个代表一元负号的伪记号）没有结合性，并且处于最高优先级。
（这里我们没有右结合运算符，如果有，可以使用 %right 来声明。）

Yacc 为每条规则赋予其右部最右端记号的优先级；如果规则不包含任何已声明优先级的记号，那么该规则自身就没有优先级。

当 Yacc 遇到因语法歧义而产生的移进-归约冲突时，它会查阅优先级表。如果冲突所涉及的所有规则都包含了在优先级声明中出现的记号，Yacc 就会使用优先级来解决冲突。

在我们的语法中，所有冲突都发生在 expression OPERATOR expression 这种形式的规则里。因此，为这四个运算符设置优先级就足以解决所有冲突。

使用显式优先级的解析器，比使用额外规则实现隐式优先级的解析器略小且略快，因为它需要归约的规则更少。

%token NAME NUMBER
%left '-' '+'
%left '*' '/'
%nonassoc UMINUS
%%
statement: NAME '=' expression
         | expression { printf("= %d\n", $1); }
         ;

expression: expression '+' expression { $$ = $1 + $3; }
          | expression '-' expression { $$ = $1 - $3; }
          | expression '*' expression { $$ = $1 * $3; }
          | expression '/' expression
            {
              if ($3 == 0)
                yyerror("divide by zero");
              else
                $$ = $1 / $3;
            }
          | '-' expression %prec UMINUS { $$ = -$2; }  /* 一元负号 */
          | '(' expression ')' { $$ = $2; }
          | NUMBER { $$ = $1; }
          ;
%%

一元负号规则 '-' expression 中包含了 %prec UMINUS 声明。虽然这条规则里唯一的运算符是 '-'（它本身的优先级很低），但我们希望一元负号的优先级高于乘法，而不是低于。

%prec 指示 Yacc 在这条规则中使用 UMINUS 的优先级（即 %nonassoc UMINUS 所声明的最高优先级），从而正确实现了 -2 * 3 被解析为 (-2) * 3 而不是 -(2 * 3)。

何时不应使用优先级规则 When Not to Use Precedence Rules

你可以用优先级规则来解决语法中出现的任何移进-归约冲突，但这通常是个糟糕的主意。

在上面提到的表达式语法(expression grammar)中，冲突的根源很容易理解，优先级规则的效果也很清晰。但在其他情况下，优先级规则虽然“修复”了移进-归约问题，却往往难以理解它们对语法实际产生了什么影响。

我们建议仅在两种情况下使用优先级规则：

表达式语法(expression grammar) 中。
解决 if-then-else 语言结构中悬空 else（dangling else） 的冲突（参见第 7 章示例）。

除此之外，如果可能，你应该修复语法本身来消除冲突。

请记住，冲突意味着 Yacc 无法正确解析该语法，很可能是因为语法存在歧义性，即同一输入对应多种可能的解析方式。除了上述两种情况，这通常意味着你的语言设计存在缺陷。如果一个语法对 Yacc 来说是歧义的，那么对人来说几乎也肯定是歧义的。

更多关于发现和修复冲突的信息，请参阅第 8 章。

变量与有类型的记号 Variables and Typed Tokens

接下来，我们将扩展计算器以支持单字母名称的变量。由于只有 26 个字母（暂时只使用小写），我们可以简单地将变量存储在一个包含 26 个元素的数组中，称之为 vbltable。

为了让计算器更实用，我们还会扩展它，使其能够处理多行表达式（每行一个），并使用浮点数值。具体实现如示例 3-2 和 3-3 所示。

Example 3-2. Calculator grammar with variables and real values ch3-03.y

%{
double vbltable[26]; /* 变量表：存储26个字母变量的值 */
%}

%union {
    double dval;  /* 用于NUMBER和expression的值类型 */
    int vblno;    /* 用于NAME的值类型（变量索引：0-25） */
}

%token <vblno> NAME     /* NAME记号的值类型为vblno（变量索引） */
%token <dval> NUMBER    /* NUMBER记号的值类型为dval（双精度浮点数） */

%left '-' '+'
%left '*' '/'
%nonassoc UMINUS

%type <dval> expression  //you must declare the value type of each nonterminal symbol for which values are used.  
                        //https://www.gnu.org/software/bison/manual/html_node/Type-Decl.html

%%
statement_list: statement '\n'
              | statement_list statement '\n'  /* 支持多行语句 */
              ;

statement: NAME '=' expression { vbltable[$1] = $3; }  /* 赋值：将表达式值存入变量表 */
         | expression { printf("= %g\n", $1); }         /* 表达式：直接打印结果 */
         ;

expression: expression '+' expression { $$ = $1 + $3; }
          | expression '-' expression { $$ = $1 - $3; }
          | expression '*' expression { $$ = $1 * $3; }
          | expression '/' expression
            {
              if ($3 == 0.0)
                yyerror("divide by zero");
              else
                $$ = $1 / $3;
            }
          | '-' expression %prec UMINUS { $$ = -$2; }   /* 一元负号 */
          | '(' expression ')' { $$ = $2; }            /* 括号 */
          | NUMBER                                      /* 数字常量 */
          | NAME { $$ = vbltable[$1]; }                 /* 变量：从变量表取值 */
          ;
%%

Example 3-3. Lexer for calculator with variables and real values ch3-03.l

%{
#include "y.tab.h"
#include <math.h>
extern double vbltable[26];
%}

%%
([0-9]+|([0-9]*\.[0-9]+)([eE][-+]?[0-9]+)?) {
    yylval.dval = atof(yytext);  /* 将数字字符串转换为double */
    return NUMBER;
}

[ \t] ; /* 忽略空白字符 */

[a-z] {
    yylval.vblno = yytext[0] - 'a';  /* 计算变量索引：a->0, b->1, ..., z->25 */
    return NAME;
}

"$" { return 0; /* 输入结束标记 */ }

\n |
. return yytext[0];  /* 换行符和其他单个字符直接返回 */
%%

符号值与 %union

我们现在有了多种类型的符号值：

表达式（expression）的值是 double 类型。
变量引用和 NAME 记号的值是 int 类型（0 到 25），对应变量表 vbltable 中的索引。

为什么不直接让词法分析器返回变量的 double 值，以使解析器更简单？

问题在于，变量名可能出现在两种不同的上下文中：

作为表达式的一部分：此时我们需要变量的 double 值。
在等号左侧（赋值语句中）：此时我们需要记住它是哪个变量，以便更新 vbltable 中对应的条目。

因此，词法分析器只能返回变量的索引（vblno），而由解析器根据上下文决定是使用该索引来取值（表达式上下文）还是赋值（赋值语句上下文）。这就是为什么需要 %union 来支持多种值类型。

为了定义可能的符号类型，我们在定义部分添加一个 %union 声明：

  //The %union declaration specifies the entire collection of possible data types for semantic values. 
  //The keyword %union is followed by braced code containing the same thing that goes inside a union in C.
  //https://www.gnu.org/software/bison/manual/html_node/Union-Decl.html
%union {
    double dval;  /* 用于数字和表达式值的类型 */
    int vblno;    /* 用于变量索引的类型 */
}

这个声明的内容会被原封不动地复制到输出文件中，作为定义 YYSTYPE 类型的 C 语言 union 声明的一部分。生成的头文件 y.tab.h 也包含该定义，以便你可以在词法分析器中使用。

下面是基于这个语法生成的 y.tab.h 文件内容示例：

#define NAME    257
#define NUMBER  258
#define UMINUS  259

typedef union {
    double dval;
    int vblno;
} YYSTYPE;

extern YYSTYPE yylval;

生成的文件还会：

声明外部变量 yylval。
为语法中的符号化记号（NAME、NUMBER、UMINUS）定义对应的记号编号（Token Numbers）（通常从 257 开始，以避免与单字符记号的 ASCII 值冲突）。

现在我们需要告诉解析器每个符号用什么类型的值。做法是：在定义符号的那一行，用尖括号 <> 标出 %union 里对应的字段名。

%token <vblno> NAME     /* NAME 的值类型是 vblno（变量编号）*/
%token <dval> NUMBER    /* NUMBER 的值类型是 dval（双精度浮点数）*/
%type <dval> expression /* expression 的值类型是 dval */

新出现的 %type 是用来给非终结符(non-terminal symbols)设置类型的——这类符号本来不需要声明，但如果你想指定它的值类型，就得用 %type。
你也可以在 %left、%right 或 %nonassoc 后面加尖括号来指定类型。
在动作代码里，Yacc 会自动给符号值加上正确的字段名。比如，如果第三个符号是 NUMBER，那么 $3 就相当于 $3.dval。

新的、功能扩展后的解析器代码如示例 3-2 所示。
我们添加了一个新的开始符号（Start Symbol） statement_list，这样解析器就能接受一个语句列表（每个语句以换行符结束），而不仅仅是单个语句。
我们还为设置变量的规则添加了对应的行为（Action），并在最后添加了一条新规则：当出现一个 NAME 时，通过从变量表中取出其对应的值，将它转换成一个表达式（expression）。

我们需要对词法分析器做一点修改（见示例 3-3）。词法分析器开头的代码块里不再声明 yylval，因为它的声明现在已经放在 y.tab.h 中了。词法分析器没有自动将类型与记号关联的机制，所以当你给 yylval 赋值时，必须明确指定使用哪个字段。
我们使用了第 2 章中的实数匹配模式来匹配浮点数。动作代码用 atof() 读取数字，然后将值赋给 yylval.dval，因为解析器期望数字值放在 dval 字段中。对于变量，我们将变量在变量表中的索引（0-25）通过 yylval.vblno 返回。
最后，我们把换行符 "\n" 设为一个常规记号，因此改用美元符号 "$" 来表示输入结束。

简单测试一下，可以看到我们修改后的计算器能正常工作了：

% ch3-03
2/3
= 0.666667
a = 2/7
a
= 0.285714
z = a+1
z
= 1.28571
a/z
= 0.222222
$

符号表 Symbol Tables

很少有用户会满足于仅使用单字符变量名，因此我们现在需要添加支持更长变量名的能力。这就意味着我们需要一个符号表（Symbol Table）。
符号表是一种数据结构，用于跟踪程序中正在使用的名称。每当词法分析器从输入中读取一个名称时，它会在符号表中查找该名称，并获取一个指向对应符号表条目（Symbol Table Entry） 的指针。
在程序的其他地方，我们都使用这个符号表指针，而不是直接使用名称字符串。因为相比每次需要时都去查找名称，使用指针要简单和快速得多。

由于符号表需要一个在词法分析器和解析器之间共享的数据结构，我们创建了一个头文件 ch3hdr.h（见示例 3-4）。
这个符号表是一个结构体数组，每个结构体包含变量的名称和它的值。
我们还声明了一个函数 symlook()，它接收一个字符串形式的名称作为参数，并返回一个指向对应符号表条目的指针。如果该名称在符号表中尚不存在，symlook() 会将其添加进去。

Example 3-4. Header for parser with symbol table ch3hdr.h

#define NSYMS 20 /* maximum number of symbols */
struct symtab {
  char *name;
  double value;
} symtab[NSYMS];
struct symtab *symlook();

解析器为使用符号表所做的改动很小，如示例 3-5 所示。
现在，NAME 记号的值是一个指向符号表的指针，而不再是之前的索引。我们修改了 %union，将指针字段命名为 symp。相应地，NAME 的 %token 声明也做了修改。那些对变量进行赋值和读取的行为（Actions），现在将记号值作为指针使用，以便它们能够读取或写入符号表条目中的 value 字段。

新的函数 symlook() 定义在 Yacc 规范文件的用户子程序部分（如示例 3-6 所示）。（这并没有特别的理由；它同样可以定义在 Lex 文件或一个独立的文件中。）
该函数通过顺序搜索符号表，来查找与传入的名称参数对应的条目。如果某个条目的名称字符串非空且与 symlook() 正在查找的名称匹配，则返回指向该条目的指针（说明该名称已被录入表中）。
如果某个条目的名称字段为空，说明我们已经遍历了所有已使用的表条目，但还没有找到这个符号。因此，我们将这个名称录入到这个此前为空的表条目中。

我们使用 strdup() 来为名称字符串创建一个永久的副本。
当词法分析器调用 symlook() 时，它传递的是记号缓冲区 yytext 中的名称。由于后续的每个记号都会覆盖 yytext 的内容，我们需要在这里自行复制一份副本。（这是在 Lex 扫描器中常见的错误来源：如果你在扫描器处理下一个记号后还需要使用 yytext 的内容，务必制作一个副本。）
最后，如果当前的符号表条目已被使用但与查找的名称不匹配，symlook() 会继续搜索下一个条目。

这个符号表例程对于当前这个简单的例子来说完全够用，但更贴近实际的符号表代码通常会复杂一些。
对于规模稍大的符号表，顺序搜索的速度太慢了，因此需要使用哈希或其他更快的搜索算法。
真实的符号表在每个条目中往往需要携带更多信息，例如：

变量的类型。
它是一个简单变量、数组还是结构体。
如果是数组，它的维度是多少。

Example 3-5. Rules for parser with symbol table ch3-04.y

%{
#include "ch3hdr.h"
#include <string.h>
%}

%union {
    double dval;          /* 用于数字和表达式结果的类型 */
    struct symtab *symp;  /* 用于NAME记号的类型：指向符号表条目的指针 */
}

%token <symp> NAME       /* NAME记号的值是指向符号表的指针 */
%token <dval> NUMBER     /* NUMBER记号的值是双精度浮点数 */

%left '-' '+'
%left '*' '/'
%nonassoc UMINUS

%type <dval> expression  /* 表达式的结果是双精度浮点数 */

%%

statement_list: statement '\n'
              | statement_list statement '\n'  /* 支持多行语句 */
              ;

statement: NAME '=' expression { $1->value = $3; }  /* 赋值：将表达式值存入符号表 */
         | expression { printf("= %g\n", $1); }     /* 表达式：直接打印结果 */
         ;

expression: expression '+' expression { $$ = $1 + $3; }
          | expression '-' expression { $$ = $1 - $3; }
          | expression '*' expression { $$ = $1 * $3; }
          | expression '/' expression
            {
              if ($3 == 0.0)
                yyerror("divide by zero");
              else
                $$ = $1 / $3;
            }
          | '-' expression %prec UMINUS { $$ = -$2; }  /* 一元负号 */
          | '(' expression ')' { $$ = $2; }           /* 括号 */
          | NUMBER                                    /* 数字常量 */
          | NAME { $$ = $1->value; }                  /* 变量：从符号表取值 */
          ;

%%

/* 查找符号表条目，如果不存在则添加 */
struct symtab *
symlook(s)
char *s;
{
    char *p;
    struct symtab *sp;
    
    for(sp = symtab; sp < &symtab[NSYMS]; sp++) {
        /* 是否已存在？ */
        if(sp->name && !strcmp(sp->name, s))
            return sp;
        
        /* 是否为空闲条目？ */
        if(!sp->name) {
            sp->name = strdup(s);  /* 复制名称字符串 */
            return sp;
        }
        /* 否则继续检查下一个 */
    }
    
    yyerror("Too many symbols");  /* 符号表已满 */
    exit(1);  /* 无法继续执行 */
} /* symlook */

词法分析器也只需做少量修改来适应符号表（如示例 3-7 所示）。它不再直接声明符号表，而是改为包含 ch3hdr.h 头文件。
识别变量名的规则现在匹配 "[A-Za-z][A-Za-z0-9]*"，即以字母开头，后跟任意字母或数字的字符串。
它的动作调用 symlook() 来获取指向符号表条目的指针，并将该指针存储在 yylval.symp 中，作为该记号的值。

Example 3-7. Lexer with symbol table ch3-04.l

%{
#include "y.tab.h"
#include "ch3hdr.h"
#include <math.h>
%}

%%
([0-9]+|([0-9]*\.[0-9]+)([eE][-+]?[0-9]+)?) {
    yylval.dval = atof(yytext);  /* 转换为浮点数 */
    return NUMBER;
}

[ \t] ; /* 忽略空白字符 */

[A-Za-z][A-Za-z0-9]* {  /* 匹配变量名：字母开头，后接字母或数字 */
    yylval.symp = symlook(yytext);  /* 获取符号表指针 */
    return NAME;
}

"$" { return 0; }  /* 输入结束标记 */

\n | . return yytext[0];  /* 换行符和其他字符直接返回 */
%%

我们的符号表例程在一个小方面比大多数编程语言中的实现更好：由于我们动态分配字符串空间，因此变量名的长度没有固定限制。

% ch3-04
foo = 12
foo /5
= 2.4
thisisanextremelylongvariablenamewhichnobodywouldwanttotype = 42
3 * thisisanextremelylongvariablenamewhichnobodywouldwanttotype
= 126
$
%

函数与保留字

接下来，我们将为计算器添加数学函数功能，包括平方根、指数和对数。我们希望计算器能够处理如下输入：

s2 = sqrt(2)
s2
= 1.41421
s2*s2
= 2

暴力实现方法的做法是：将每个函数名都定义为独立的记号（Token），并为每个函数添加单独的语法规则。例如：

%token SQRT LOG EXP  /* 声明函数名对应的记号 */

expression: SQRT '(' expression ')' { $$ = sqrt($3); }
          | LOG '(' expression ')'  { $$ = log($3); }
          | EXP '(' expression ')'  { $$ = exp($3); }
          | ... /* 其他表达式规则 */
          ;

这种方法虽然直观，但当函数数量增多时，会导致语法规则急剧膨胀。更优雅的方式是使用符号表将函数名识别为一种特殊的“函数调用”结构，但当前示例采用了这种简单的直接规则方式。

符号表中的保留字

首先，我们把函数名的具体匹配模式从词法分析器（Lexer） 中移出，放入符号表（Symbol Table） 中。
我们在每个符号表条目里添加一个新字段：funcptr。如果这个条目对应的是一个函数名，那么 funcptr 就是一个指向要调用的 C 函数的指针。

struct symtab {
  char *name;
  double (*funcptr)();
  double value;
} symtab[NSYMS];

我们需要在解析器开始工作之前就把函数名预先添加到符号表里。为此，我们编写了自己的 main() 函数，它在调用 yyparse() 之前，先调用一个新的例程 addfunc()，将每个函数名添加到符号表。
addfunc() 的代码很简单：它获取一个名称对应的符号表条目，然后设置其 funcptr 字段。

main()
{
    extern double sqrt(), exp(), log();
    
    addfunc("sqrt", sqrt);
    addfunc("exp", exp);
    addfunc("log", log);
    
    yyparse();
}

addfunc(name, func)
char *name;
double (*func)();
{
    struct symtab *sp = symlook(name);
    sp->funcptr = func;
}

我们定义了一个新的记号 FUNC 来代表函数名。词法分析器在看到一个函数名时会返回 FUNC，而在看到一个变量名时则返回 NAME。无论是哪种情况，它们的值都是指向符号表的指针。

在解析器中，我们用一个通用的函数规则替换了原来为每个函数单独写的规则：

%token <symp> NAME FUNC  /* NAME 和 FUNC 记号的值都是符号表指针 */

%%
expression: ...
          | FUNC '(' expression ')' { $$ = ($1->funcptr)($3); }  /* 通用函数调用 */
          ;

当解析器看到一个函数引用时，它会查询该函数对应的符号表条目，从而找到实际要调用的内部函数指针。
在词法分析器中，我们移除了显式匹配函数名的模式，并修改了识别名称的动作代码：如果符号表条目表明该名称是一个函数名，则返回 FUNC 记号。

[A-Za-z][A-Za-z0-9]* {
    struct symtab *sp = symlook(yytext);
    yylval.symp = sp;
    
    if (sp->funcptr)  /* 它是一个函数吗？ */
        return FUNC;
    else
        return NAME;
}

这些修改产生了一个与之前功能相同的程序，但函数名现在存储在符号表中。这样做的好处是，程序可以在解析过程中动态地添加新的函数名。

可互换的函数名与变量名

最后一个改动在技术上很小，但从语言特性角度看却是个重大变化：没有理由要求函数名和变量名必须不同。解析器完全可以通过语法结构来区分函数调用和变量引用。

因此，我们把词法分析器改回原来的样子：对于任何名称，始终返回 NAME 记号。然后，我们修改解析器，允许在函数调用的位置使用 NAME：

%token <symp> NAME
%%
expression: ...
          | NAME '(' expression ')' { ... }  /* 允许 NAME 出现在函数调用位置 */

完整的程序见示例 3-8 至 3-11。如示例 3-9 所示，我们不得不添加一些错误检查，以确保当用户调用一个“函数”时，它确实是一个真正的函数。

现在，计算器的操作方式和之前一样，只是函数名和变量名可以重合了。

% ch3-05
sqrt(3)
= 1.73205
foo(3)
foo not a function
= 0
sqrt = 5
sqrt(sqrt)
= 2.23607

关于是否应该允许用户在同一个程序中对两个不同的东西使用相同的名称，这是个有争议的问题。一方面，这可能使程序更难理解；另一方面，如果不允许，用户就不得不绞尽脑汁去发明不与保留字冲突的名称。

两种做法都可能走向极端。COBOL 有超过 300 个保留字，以至于没人能全部记住，程序员不得不采用奇怪的惯例，比如让每个变量名都以数字开头，以确保不发生冲突。而另一方面，PL/I 则根本没有保留字，因此你可以写出这样的代码：

IF IF = THEN THEN ELSE = THEN; ELSE ELSE = IF;

示例 3-8. 最终版计算器头文件 ch3hdr2.h

#define NSYMS 20 /* 符号的最大数量 */

struct symtab {
    char *name;               /* 符号名 */
    double (*funcptr)();      /* 函数指针（如果是函数） */
    double value;             /* 值（如果是变量） */
} symtab[NSYMS];

struct symtab *symlook();

示例 3-9. 最终版计算器解析器规则 ch3-05.y

%{
#include "ch3hdr2.h"
#include <string.h>
#include <math.h>
%}

%union {
    double dval;
    struct symtab *symp;
}

%token <symp> NAME
%token <dval> NUMBER
%left '-' '+'
%left '*' '/'
%nonassoc UMINUS
%type <dval> expression

%%
statement_list: statement '\n'
              | statement_list statement '\n'
              ;

statement: NAME '=' expression { $1->value = $3; }
         | expression { printf("= %g\n", $1); }
         ;

expression: expression '+' expression { $$ = $1 + $3; }
          | expression '-' expression { $$ = $1 - $3; }
          | expression '*' expression { $$ = $1 * $3; }
          | expression '/' expression
            {
              if ($3 == 0.0)
                yyerror("divide by zero");
              else
                $$ = $1 / $3;
            }
          | '-' expression %prec UMINUS { $$ = -$2; }
          | '(' expression ')' { $$ = $2; }
          | NUMBER
          | NAME { $$ = $1->value; }
          | NAME '(' expression ')' {  /* 函数调用 */
              if ($1->funcptr)
                $$ = ($1->funcptr)($3);
              else {
                printf("%s not a function\n", $1->name);
                $$ = 0.0;
              }
            }
          ;
%%

示例 3-10. 最终版计算器解析器的用户子程序 ch3-05.y

/* 查找符号表条目，不存在则添加 */
struct symtab *
symlook(s)
char *s;
{
    char *p;
    struct symtab *sp;
    
    for (sp = symtab; sp < &symtab[NSYMS]; sp++) {
        /* 是否已存在？ */
        if (sp->name && !strcmp(sp->name, s))
            return sp;
        
        /* 是否为空闲条目？ */
        if (!sp->name) {
            sp->name = strdup(s);
            return sp;
        }
        /* 否则继续检查下一个 */
    }
    
    yyerror("Too many symbols");
    exit(1); /* 无法继续 */
}

addfunc(name, func)
char *name;
double (*func)();
{
    struct symtab *sp = symlook(name);
    sp->funcptr = func;
}

main()
{
    extern double sqrt(), exp(), log();
    
    addfunc("sqrt", sqrt);
    addfunc("exp", exp);
    addfunc("log", log);
    
    yyparse();
}

示例 3-11. 最终版计算器词法分析器 ch3-05.l

%{
#include "y.tab.h"
#include "ch3hdr2.h"
#include <math.h>
%}

%%
([0-9]+|([0-9]*\.[0-9]+)([eE][-+]?[0-9]+)?) {
    yylval.dval = atof(yytext);
    return NUMBER;
}

[ \t] ; /* 忽略空白字符 */

[A-Za-z][A-Za-z0-9]* { /* 返回符号表指针 */
    struct symtab *sp = symlook(yytext);
    yylval.symp = sp;
    return NAME;
}

"$" { return 0; } /* 结束输入 */

\n |
. return yytext[0];
%%

使用 Make 构建解析器

当你第三次手动重新编译这个例子时，你大概就会想到应该使用 UNIX 的 make 工具来自动化这个编译过程了。控制这个过程的 Makefile 如示例 3-12 所示。

示例 3-12. 计算器的 Makefile

#LEX = flex -I
#YACC = byacc
CC = cc -DYYDEBUG=1

ch3-05: y.tab.o lex.yy.o
    $(CC) -o ch3-05 y.tab.o lex.yy.o -ly -ll -lm

lex.yy.o: lex.yy.c y.tab.h
lex.yy.o y.tab.o: ch3hdr2.h

y.tab.c y.tab.h: ch3-05.y
    $(YACC) -d ch3-05.y

lex.yy.c: ch3-05.l
    $(LEX) ch3-05.l

说明：

最上面的两行被注释的赋值语句，可以用来将 lex 替换为 flex、yacc 替换为 Berkeley 的 byacc。Flex 需要 -I 标志来告诉它生成一个交互式扫描器（遇到换行符时不向前预读）。
CC 宏定义了预处理器符号 YYDEBUG=1，这会编译一些调试代码，对测试解析器很有用。
将一切编译链接成 ch3-05 的规则引用了三个库：
- -ly：yacc 库（提供 yyerror() 和早期版本中的 main()）
- -ll：lex 库（提供 lex 扫描器需要的内部支持例程；由 flex 生成的扫描器不需要它，但留着也没坏处）
- -lm：数学库（提供 sqrt()、exp() 和 log()）

如果使用 Bison（GNU 的 yacc 版本）
由于 Bison 使用不同的默认文件名，我们需要修改生成 y.tab.c 的规则：

y.tab.c y.tab.h: ch3-05.y
    bison -d ch3-05.y
    mv ch3-05.tab.c y.tab.c
    mv ch3-05.tab.h y.tab.h

（或者，我们可以修改 Makefile 的其余部分和代码，使用 Bison 更易记的文件名；也可以使用 -y 选项告诉 Bison 使用标准的 yacc 文件名。）

关于 make 的更多细节，可以参考 Steve Talbott 的《Managing Projects with Make》（O'Reilly & Associates 出版）。

posted @ 2026-01-22 15:11 dewxin 阅读(8) 评论(0) 收藏举报

刷新页面返回顶部

Dewxin