WQS二分
[dp 进阶] WQS 二分
对于定义域为整数的函数 \(f(x)\),如果其差分 \(\Delta f(x)\) 单调,则称 \(f(x)\) 为凸函数。如果 \(\Delta f(x)\) 单调减,则称 \(f(x)\) 上凸,否则称 \(f(x)\) 下凸。
wqs 二分可以用来解决有关凸函数的问题。下面假设凸函数指下凸函数,上凸函数的情况类似。
已知一个函数 \(f(x)\) 是凸的,我们要求出它在某一点 \(m\) 处的取值 \(f(m)\),但我们无法直接求出。然而,我们能够求出函数的全局最小值。为了求出 \(f(m)\),我们把 \(f(x)\) 加上一个一次函数,设新函数为 \(F(x)\)。可以证明 \(F(x)\) 仍然下凸。如果能找到一个合适的一次函数,就可以使得 \(F(m)\) 是全局的最小值,这时就可以求出 \(F(m)\),进而求出 \(f(m)\)。
以上就是 wqs 二分的核心思想。在实际的问题中,往往需要我们把问题建模成有关凸函数极值的问题再求解,这类问题常常包含”恰好选择 \(m\) 个“等字眼。
具体的例子
这么说比较抽象,我们以一个题为例:
(P4983 忘情)(略有改动)给定一个长度为 \(n\) 的整数序列 \(a\),你需要把它划分成恰好 \(m\) 段。每段的权值为该段元素的和的平方,你需要最小化 \(m\) 段的权值之和。
\(1 \le m \le n \le 10^{5}\),\(a_{i} \le 1000\)。
容易想到这样的 dp:设 \(dp(i, j)\) 表示把前 \(i\) 个元素分为 \(j\) 段的最小代价,暴力转移的时间复杂度为 \(O(n^{2}m)\)。使用斜率优化可以做到 \(O(nm)\),和状态数相同。
接下来还能怎么优化呢?我们先抛弃 dp 的转移方程,感性地理解最优决策:如果没有恰好分成 \(m\) 段的限制,那么最优方案一定是划分成 \(n\) 段,即每个元素单独一段。这是容易证明的:由于元素都是正数,合并任意的两段都会产生额外的代价。
为了处理”恰好分成 \(m\) 段“的限制,我们考虑这样的策略:给分段设置一个附加的代价 \(c\)。也就是说每新分出一段,就需要多花费 \(c\) 的代价。那么最优解应当在”段数多,附加代价多“和”段数少,原来的代价多“之间找到平衡。我们期望能找到合适的 \(c\),使得最优解恰好是分成 \(m\) 段。此时把最优解的代价减去 \(mx\) 就能得到正确的答案。
加上这个限制之后,我们就不必在状态中记录分了几段,因此可以 \(O(n)\) dp。那么我们只要能找到合适的 \(c\),问题就解决了。
这种策略看上去比较玄学,但通过把问题抽象成函数模型,我们可以严谨证明这是正确的。下面我们来具体解释为什么。
建模成凸函数
设 \(f(x)\) 表示把序列恰好分成 \(x\) 段的最小代价,那么答案即为 \(f(m)\)。我们无法求出 \(f(x)\) 在某个特定点的取值,但可以求出它的全局最小值。
我们可以证明:\(f(x)\) 是一个下凸函数。
证明
暂略
现在犀利的东西来了:如果给分段设置一个附加的代价 \(c\),那么函数中的每个值 \(f(x)\) 都会增加 \(cx\),这是显然的。这就相当于给 \(f(x)\) 加上了一个一次函数 \(g(x) = cx\)。设 \(F(x) = f(x) + g(x)\),容易证明 \(F(x)\) 仍然是下凸函数。(\(f(x)\) 的差分单调增,\(g(x)\) 的差分为常数,二者和的差分仍然单调增,因此 \(F(x)\) 下凸。)
我们仍然可以用 dp 求出 \(F(x)\) 的全局最小值,但是,使得 \(f(x)\) 和 \(F(x)\) 取到最小值的 \(x\) 可能不相同!如果能找到合适的 \(c\),使得 \(F(x)\) 在 \(x = m\) 时取到最小值,那么我们就求出了答案。
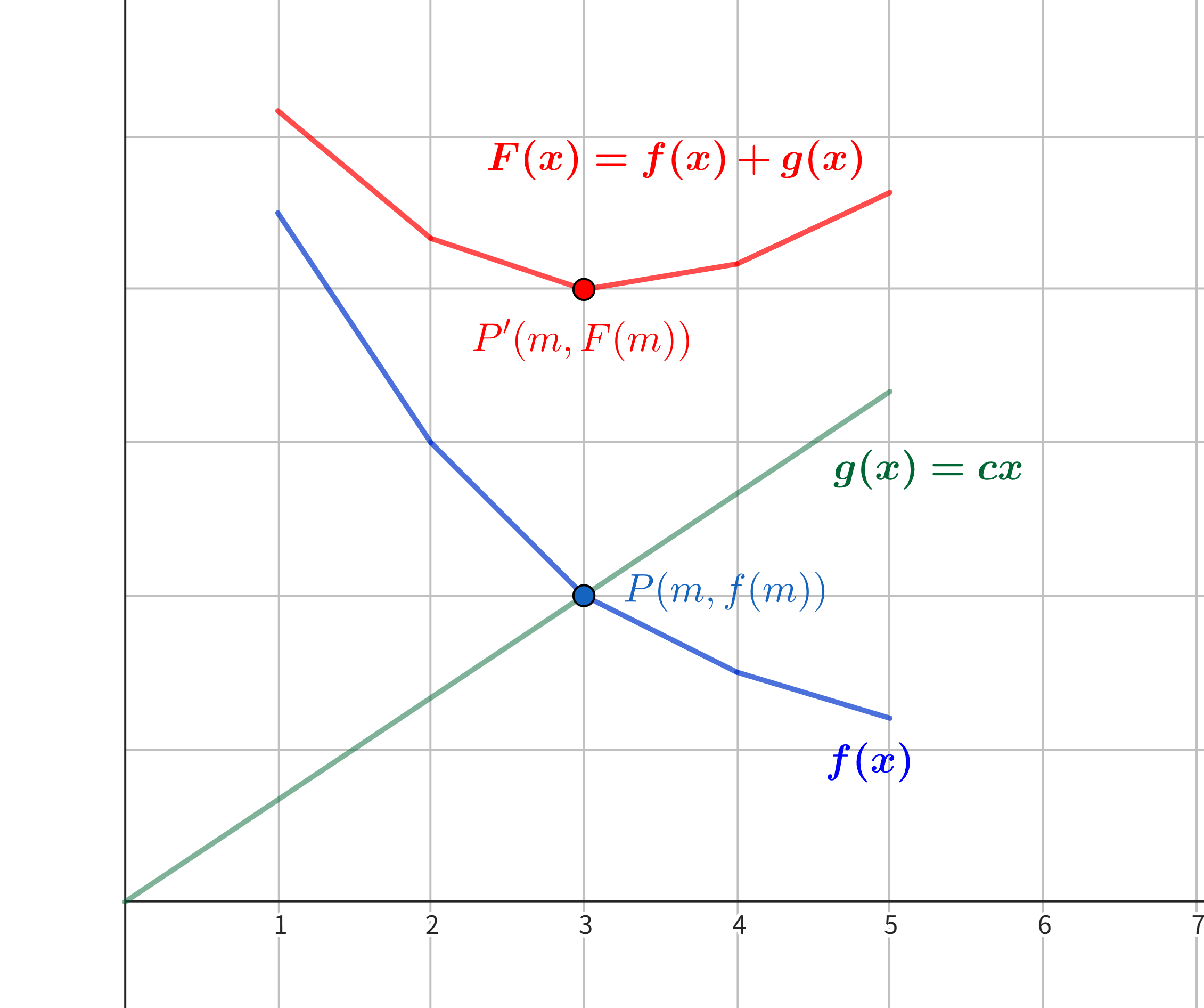
如图,蓝线代表 \(f(x)\),绿线代表 \(g(x) = cx\),红线代表 \(F(x) = f(x) + g(x)\)。通过加上合适的 \(cx\),我们使得 \(F(x)\) 在 \(x = m\) 处取得了最小值。
用函数建模以后,把 \(F(m)\) 减去 \(c \cdot m\) 得到答案的正确性就很明显了。剩下的问题是:如何求出合适的 \(c\)?
对斜率二分
把 \(f(x)\) 加上 \(cx\) 再求全局最小值,实际上等价于:用一条斜率为 \(-c\) 的直线切 \(f(x)\)。前者求得的最小值的 \(x\) 坐标和后者切点的 \(x\) 坐标相同。
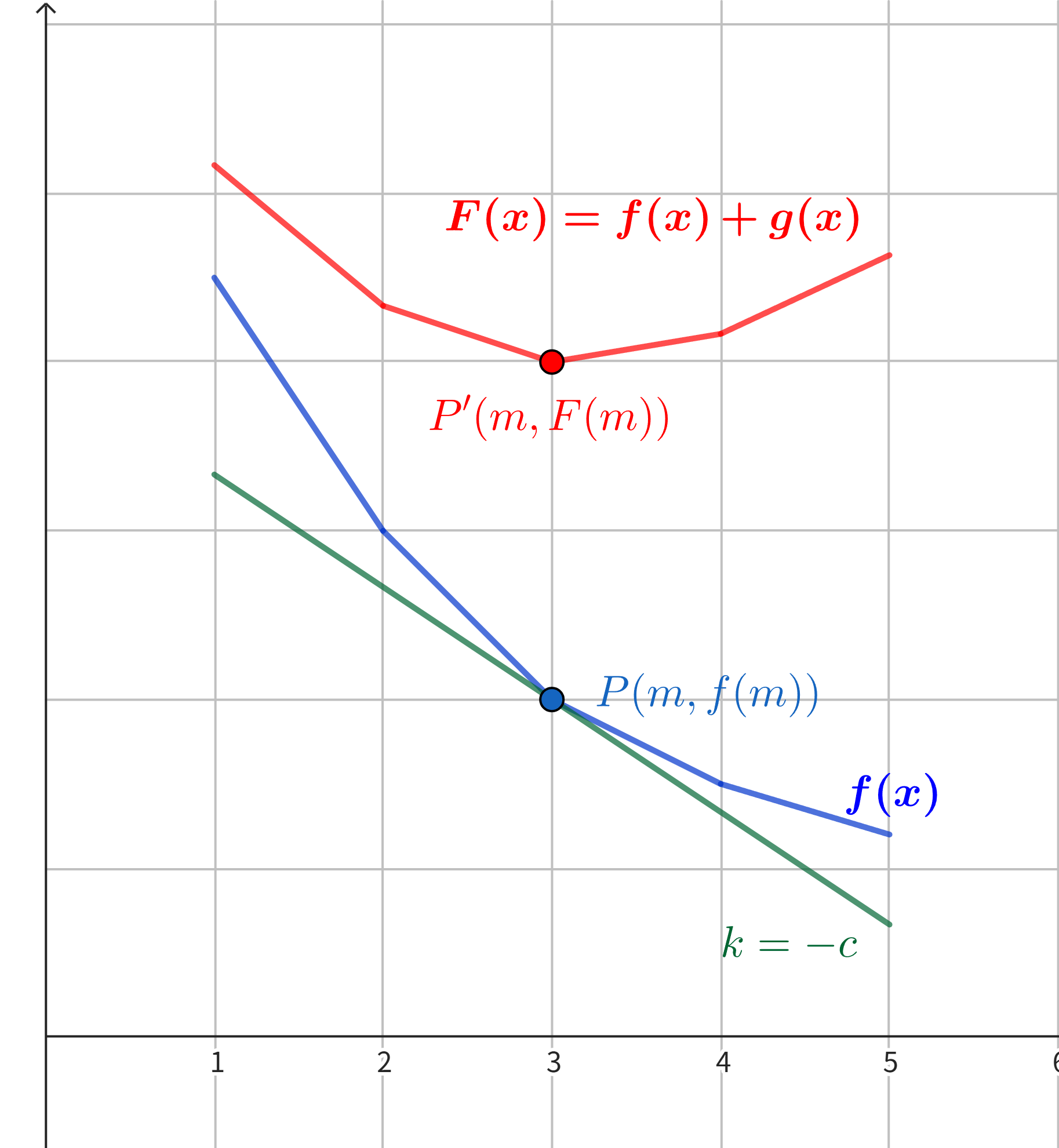
也就是说:如果能找到一条直线切 \(f(x)\) 的横坐标为 \(m\),那么它的斜率就是我们需要的 \(c\)。由于 \(f(x)\) 是凸函数,相邻两点间的斜率有单调性,所以用斜率不同的直线切 \(f(x)\) 时,切点的横坐标也有单调性。如果切点在 \(m\) 左侧,说明斜率太小;否则说明斜率太大。也可以这样理解:分的段数少(对应切点在 \(m\) 左侧),说明附加代价太大(注意,斜率和附加代价是相反数的关系);否则说明附加代价太小。
由于有这种单调性,我们就可以二分斜率(或者说二分附加代价),找到合适的 \(c\)。这也证明了 WQS 二分的正确性:由于函数有凸性,所以一定存在一条直线切 \(f(x)\) 的横坐标为 \(m\)。
以下是一些细节问题:
-
当 \(f(x)\) 的值都为整数时,相邻两点之间的斜率 \(\dfrac{f(x + 1) - f(x)}{(x + 1) - x} = f(x + 1) - f(x)\) 也是整数。因此,对于任意点都存在一条斜率为整数的切线。这样就可以规避浮点数二分,提高效率。
-
我们如何知道直线切 \(f(x)\) 的切点?在 dp 时,除了记录最小代价,我们还要记录最优决策是分了几段。 在某些题目中,我们可以把这两个信息放到一个结构体中以方便转移。这样,dp 后最优决策的段数就是切点的 \(x\) 坐标。
-
二分的边界:斜率的上下界应该大于/小于函数图象的最大/小斜率,但这么考虑比较麻烦。比较好的想法是考虑附加代价的上下界。对于例题,附加代价为 \(0\) 时段数达到最大值 \(n\),因此下界为 \(0\)。至于上界,我们需要段数达到最小值 \(1\),所以把一段分成两段减少的代价应该不足以抵消附加的代价,可以设为 \(n^{2}w^{2}\),也就是 \(10^{16}\),其中 \(w\) 是值域。
共线情况的处理
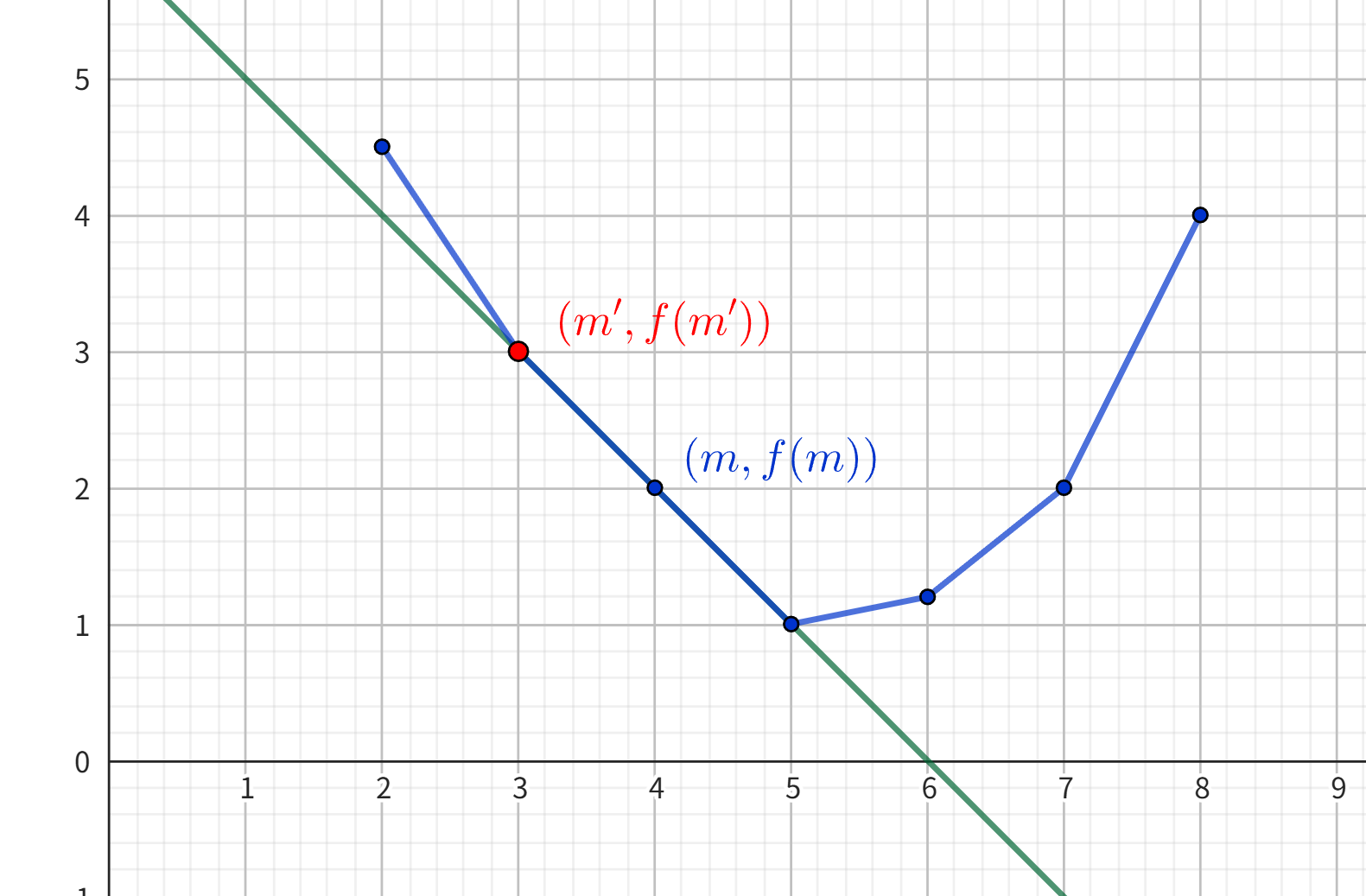
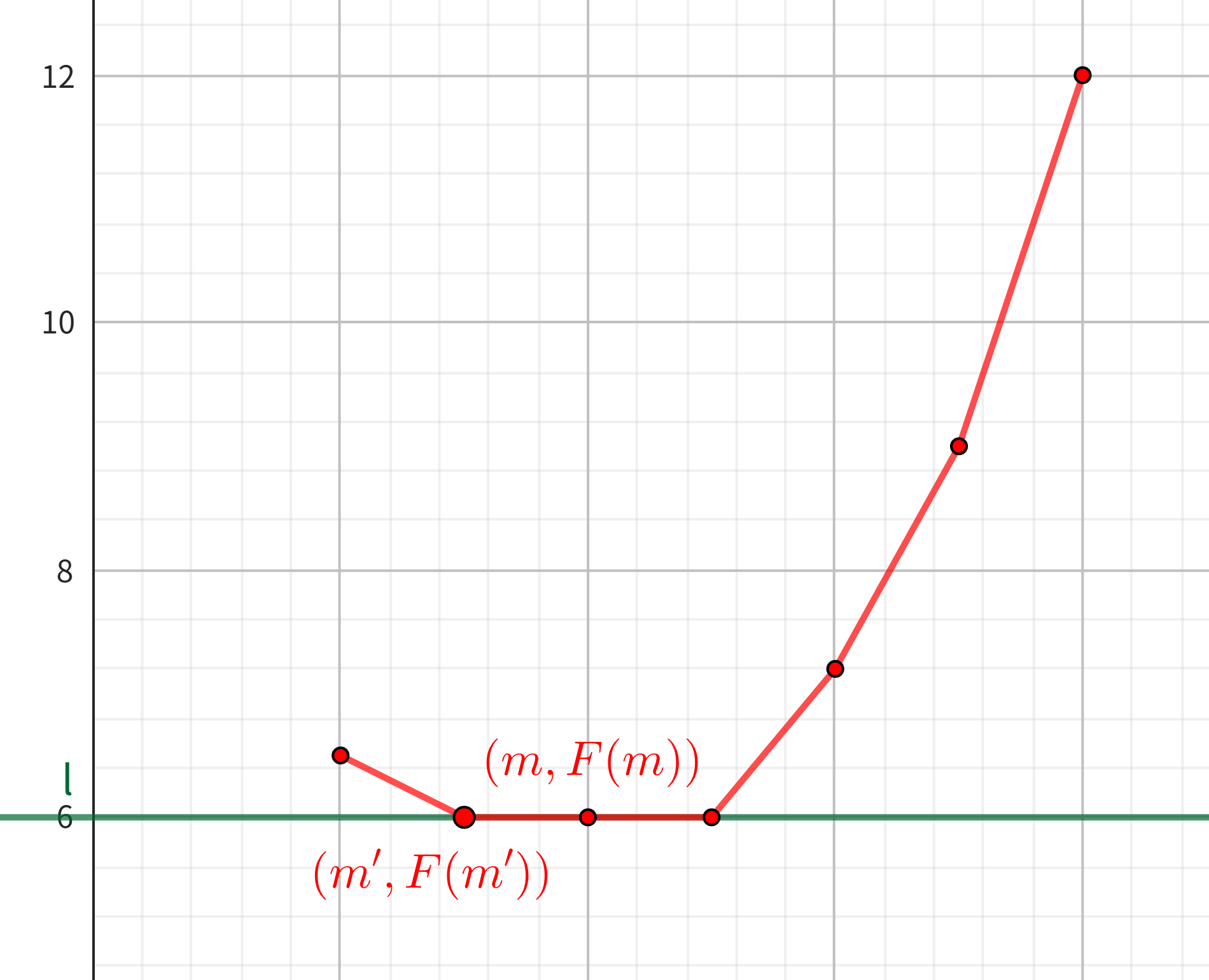
有时直线会切到不止一个点。我们在 dp 时需要遵循一个策略:如果有代价相同的决策,选择段数最少的。(或者最多的,但前后必须相同,取决于代码实现。)这就相当于:如果有不止一个切点,返回 \(x\) 坐标最小的。如果没有三点共线的情况,则一定有某次 dp 返回的段数为 \(m\),可以得出正确答案。但如果存在三点共线,那么一定不会返回 \(m\),而是返回和 \((m, f(m))\) 共线的点中 \(x\) 坐标最小的,设其 \(x\) 坐标为 \(m'\)。这种情况下,虽然切点的横坐标不是 \(m\),但计算出的代价 \(F(m') = F(m)\),所以仍然能得知 \(f(m) = F(m) - c \cdot m = F(m') - c \cdot m\)。
以下是一种参考写法:
while(lo <= hi) {
i64 mid = (lo + hi) >> 1;
auto [val, cnt] = dp(mid);
if(cnt <= m) {
ans = val - mid * m; // 注意不是 val - cnt * m
hi = mid - 1;
} else {
lo = mid + 1;
}
}
例题
I. P2619 [国家集训队] Tree I
这题不是 dp,但可以建模成凸函数。
设 \(f(x)\) 表示恰好使用了 \(x\) 条白边的最小生成树的边权和,可以证明 \(f(x)\) 下凸。
证明
暂略给白边设置附加权值,WQS 二分套 Kruskal 即可。需要注意的是,在代价相同时,要选择白边数量最少的决策。所以对于边权相同的边,优先使用黑边,可以证明这样能够得到白边数量最少的最小生成树。
Code
#include<bits/stdc++.h>
using namespace std;
constexpr int V = 100;
struct DSU {
vector<int> fa;
DSU(int n): fa(n) {
iota(fa.begin(), fa.end(), 0);
}
int getfa(int x) {
return x == fa[x] ? x : fa[x] = getfa(fa[x]);
}
bool same(int x, int y) {
return getfa(x) == getfa(y);
}
void merge(int x, int y) {
int fx = getfa(x), fy = getfa(y);
fa[fy] = fx;
}
};
struct Edge {
int u, v, w, c;
};
int main() {
cin.tie(nullptr) -> sync_with_stdio(false);
int n, m, k;
cin >> n >> m >> k;
vector<Edge> e(m);
for(auto &[u, v, w, c]: e) {
cin >> u >> v >> w >> c;
}
int cnt = 0, sum = 0;
auto kruskal = [&](int x) {
cnt = sum = 0;
DSU dsu(n);
for(auto &ed: e) {
if(ed.c == 0) {
ed.w += x;
}
}
sort(e.begin(), e.end(), [&](Edge &A, Edge &B) {
return A.w == B.w ? (A.c > B.c) : (A.w < B.w);
});
// 优先使用黑边,得到白边数量最少的最小生成树。
// 保证三点共线时求得的是最左边的点的坐标
int ecnt = 0;
for(auto [u, v, w, c]: e) {
if(dsu.same(u, v)) continue;
dsu.merge(u, v);
sum += w;
if(c == 0) cnt++;
if(++ecnt == n - 1) break;
}
for(auto &ed: e) {
if(ed.c == 0) {
ed.w -= x;
}
}
};
int lo = -(V + 1), hi = V + 1, ans = -1;
while(lo <= hi) {
int mid = (lo + hi) / 2;
kruskal(mid);
if(cnt <= k) {
// 白边选的少,说明附加权值过大
// 三点共线的情况在这里处理
hi = mid - 1;
ans = sum - k * mid;
} else {
lo = mid + 1;
}
}
cout << ans << '\n';
return 0;
}
II. P1484 种树
设 \(f(x)\) 表示种 \(x\) 棵树的最大获利,可以证明 \(f(x)\) 上凸。
这题和之前不太一样,要求种“不多于” \(k\) 棵树而不是“恰好” \(k\) 棵树。但这无伤大雅:可以先不设置附加代价 dp 一遍,如果种树不超过 \(k\) 棵就直接输出答案,否则再 WQS 二分。
内层 \(O(n)\) 的 dp 是容易的,记得在 dp 值中记录段数。一个好的方法是用结构体:
struct Node {
i64 sum;
int cnt;
bool operator < (const Node &rhs) const {
return sum == rhs.sum ? (cnt > rhs.cnt) : (sum < rhs.sum);
}
Node operator + (const Node &rhs) const {
return Node{sum + rhs.sum, cnt + rhs.cnt};
}
};
完整代码
#include<bits/stdc++.h>
using namespace std;
typedef long long i64;
constexpr int V = 1'000'000;
struct Node {
i64 sum;
int cnt;
bool operator < (const Node &rhs) const {
return sum == rhs.sum ? (cnt > rhs.cnt) : (sum < rhs.sum);
}
Node operator + (const Node &rhs) const {
return Node{sum + rhs.sum, cnt + rhs.cnt};
}
};
int main() {
cin.tie(nullptr) -> sync_with_stdio(false);
int n, k;
cin >> n >> k;
vector<int> a(n + 1);
for(int i = 1; i <= n; i++) {
cin >> a[i];
}
auto dp = [&](int x) {
// 种一棵树的附加代价为 x
vector<array<Node, 2>> f(n + 1);
f[0][0] = Node{0, 0}, f[0][1] = Node{-1, 0};
for(int i = 1; i <= n; i++) {
f[i][0] = max(f[i - 1][0], f[i - 1][1]);
f[i][1] = f[i - 1][0] + Node{a[i] - x, 1};
}
return max(f[n][1], f[n][0]);
};
int lo = 0, hi = V;
i64 ans = -1;
while(lo <= hi) {
int mid = (lo + hi) >> 1;
auto [sum, cnt] = dp(mid);
if(cnt <= k) {
hi = mid - 1;
ans = sum + 1LL * k * mid;
} else {
lo = mid + 1;
}
}
cout << ans << '\n';
return 0;
}
双倍经验:P1792 [国家集训队] 种树
显然只有当 \(2m > n\) 时才无解。剩下的只是把“不超过”改成了“恰好”,把链改成了环。对于环上 dp 的处理,参考基环树 dp 的方式,分别钦定是否在第一个位置种树,dp 两次取最优值即可。
Code
#include<bits/stdc++.h>
using namespace std;
typedef long long i64;
constexpr i64 INF = 0x3f3f3f3f'3f3f3f3f;
constexpr int V = 1000;
struct Node {
i64 sum;
int cnt;
bool operator < (const Node &rhs) const {
return sum == rhs.sum ? (cnt > rhs.cnt) : (sum < rhs.sum);
}
Node operator + (const Node &rhs) const {
return Node{sum + rhs.sum, cnt + rhs.cnt};
}
};
int main() {
cin.tie(nullptr) -> sync_with_stdio(false);
int n, m;
cin >> n >> m;
vector<int> a(n + 1);
for(int i = 1; i <= n; i++) {
cin >> a[i];
}
if(m * 2 > n) {
cout << "Error!\n";
return 0;
}
auto dp = [&](int x) {
// 种一棵树的附加代价为 x
vector<array<Node, 2>> f(n + 1);
// 钦定第一个位置不种树
f[1][1] = Node{-INF, 1};
f[1][0] = Node{0, 0};
for(int i = 2; i <= n; i++) {
f[i][0] = max(f[i - 1][0], f[i - 1][1]);
f[i][1] = f[i - 1][0] + Node{a[i] - x, 1};
}
auto res = max(f[n][0], f[n][1]);
// 钦定第一个位置种树
f[1][1] = Node{a[1] - x, 1};
f[1][0] = Node{-INF, 0};
for(int i = 2; i <= n; i++) {
f[i][0] = max(f[i - 1][0], f[i - 1][1]);
f[i][1] = f[i - 1][0] + Node{a[i] - x, 1};
}
res = max(res, f[n][0]);
return res;
};
int lo = -V - 1, hi = V + 1;
i64 ans = -1;
while(lo <= hi) {
int mid = (lo + hi) / 2;
auto [sum, cnt] = dp(mid);
if(cnt <= m) {
hi = mid - 1;
ans = sum + 1LL * m * mid;
} else {
lo = mid + 1;
}
}
cout << ans << '\n';
return 0;
}
III. [ABC218H] Red and Blue Lamps
可以证明报酬关于红灯数量的函数上凸。\(O(n)\) dp 也是显然的。
唯一值得说明的是上界的选取:设 \(w = \max A_{i}\),则附加代价的上界应 \(> 2w\)。(而不是 \(w\))因为改变一盏灯的颜色可能同时影响两侧的收益。我因为这个问题调了很久。
IV. [ABC400G] Patisserie ABC 3
问题可以转化成:
每个蛋糕有三种属性。每个蛋糕要么选择恰好一种属性,要么不选择。我们要选择总共 \(2K\) 个属性,满足每种属性选择的个数都是偶数,在此基础上最大化选择的属性的和。
可以证明最大价格总和关于选取蛋糕数量的函数上凸。
设 \(f(i, x, y, z)\) (\(x, y, z \in \{0, 1\}\))表示在前 \(i\) 个蛋糕中选取,使得 X,Y,Z 属性选取数量的奇偶性分别为 \(x, y, z\) 时的最大价格之和。转移方程显然。WQS 二分即可。
V. P4983 忘情
这就是文章开头用来引入的例题,只是略有区别。题面中的式子可以化简成 \((1 + \sum x_{i})^{2}\),也就是区间和加 \(1\) 的平方,这个 \(+1\) 基本不影响之前的讨论。WQS 二分 + 斜率优化 dp 即可。
需要指出的一点是,在斜率优化的 dp 中,怎么确保在代价相同的决策中选择段数最少的?用斜率为 \(k\) 的直线去切决策点构成的凸包,则代价相同的决策共线。最直接的方法是对所有被切到的点更新答案,这肯定是正确的,但代码有点冗长:
int j = -1;
while(head < tail && slope(que[head], que[head + 1]) <= (double)k) {
if(slope(que[head], que[head + 1]) == (double)k) {
if(j == -1 || f[que[head]].cnt < f[j].cnt) {
j = que[head];
}
}
head++;
}
if(j == -1 || f[que[head]].cnt < f[j].cnt) {
j = que[head];
}
有一种简单的写法可以通过此题,但我无法证明其正确性:
while(head < tail && slope(que[head], que[head + 1]) < (double)k) head++;
int j = que[head];
如果把 slope(que[head], que[head + 1]) < (double)k 中的 < 改成 <= 则无法通过。实际上 < 表示取共线的点中的 \(x\) 坐标最小的,而 <= 表示取 \(x\) 坐标最大的。
Code
#include<bits/stdc++.h>
#define debug(...) fprintf(stderr, __VA_ARGS__)
#define sqr(x) ((x) * (x))
using namespace std;
typedef long long i64;
struct Node {
i64 val, cnt;
};
int main() {
cin.tie(nullptr) -> sync_with_stdio(false);
// freopen("P4983.in", "r", stdin);
// freopen("x.out", "w", stdout);
int n, m;
cin >> n >> m;
vector<i64> a(n + 1);
for(int i = 1; i <= n; i++) {
cin >> a[i];
}
vector<i64> sum(n + 1);
partial_sum(a.begin() + 1, a.end(), sum.begin() + 1);
auto dp = [&](i64 x) {
// 在代价相同的决策中选择段数最小的
vector<Node> f(n + 1);
auto point = [&](int i) {
return make_pair(sum[i], f[i].val + sum[i] * sum[i] + x);
};
auto slope = [&](int i, int j) {
auto [x1, y1] = point(i);
auto [x2, y2] = point(j);
return (double)(y2 - y1) / (double)(x2 - x1);
};
vector<int> que(n + 1);
int tail = 0, head = 0;
for(int i = 1; i <= n; i++) {
i64 k = 2 * (sum[i] + 1);
int j = -1;
while(head < tail && slope(que[head], que[head + 1]) <= (double)k) {
if(slope(que[head], que[head + 1]) == (double)k) {
if(j == -1 || f[que[head]].cnt < f[j].cnt) {
j = que[head];
}
}
head++;
}
if(j == -1 || f[que[head]].cnt < f[j].cnt) {
j = que[head];
}
f[i].val = f[j].val + sqr(1 + sum[i] - sum[j]) + x;
f[i].cnt = f[j].cnt + 1;
while(head < tail && slope(que[tail], i) <= slope(que[tail - 1], que[tail])) tail--;
que[++tail] = i;
// cerr << "f[" << i << "] = " << f[i].val << ' ' << f[i].cnt << '\n';
}
return f[n];
};
i64 lo = 0, hi = (i64)(1e16) + 10, ans = -1; // hi > (n * w)^2
while(lo <= hi) {
i64 mid = (lo + hi) >> 1;
auto [val, cnt] = dp(mid);
// debug("[%lld, %lld]: mid = %lld, val = %lld, cnt = %lld\n", lo, hi, mid, val, cnt);
if(cnt <= m) {
ans = val - mid * m;
hi = mid - 1;
} else {
lo = mid + 1;
}
}
cout << ans << '\n';
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号