DP 优化方法大杂烩 I.

前方标 * 的是推荐阅读的部分或推荐做的题目。

由于文章内容过多，为分摊压力，更多内容详见 DP 优化方法大杂烩 II.。

CHANGE LOG

2021.12.21：计划重构整篇文章。当前重构至矩阵快速幂。
2021.12.22：重构至 wqs 二分。
2021.12.23：施工完毕。
2022.1.25：第二遍重构文章，修改表述。
2022.2.11：施工完毕。

0. 前言

动态规划是 OI 界的一个博大分支，因而衍生出了很多优化方法。最基本的是对 状态设计 的优化。如果状态从三维降到了两维，甚至一维，将对时间复杂度和常数产生巨大影响。

可惜的是，对状态设计的优化并没有一般性方法，全凭做题经验与观察性质的能力。文章涉及到的方法大都是对 如何转移 的优化，如根据决策单调性尝试分治。

一般用 $t$ D / $e$ D 描述动态规划规模的类型，其中 $t$ 表示问题大小， $e$ 表示转移时依赖子问题的大小。即状态数 $n^{t}$ ，每个状态依赖于 $n^{e}$ 个前驱状态的信息。除非问题有特殊性质，解决 $t$ D / $e$ D 动态规划需要 $O (n^{t + e})$ 的时间复杂度。

$1$ D / $1$ D：最长上升子序列。
2D / 0D：最长公共子序列，普通背包问题。
2D / 1D：多源最短路 Floyd。

1. 动态 DP

动态 DP 简称 DDP（Dynamic Dynamic Programming），其本质是用矩阵维护带修改的动态规划问题。

1.1 矩阵描述转移

部分动态规划转移方程涉及到的状态较少，且一个状态由其前驱的 线性组合 得到。其实并不一定需是线性组合，只需满足 结合律，见下方说明。此时可以用 矩阵乘法 描述转移方程。

斐波那契数列 $f_{i} = f_{i - 1} + f_{i - 2}$ 即一例。求解 $f_{i}$ 只需知道 $f_{i - 1}$ 和 $f_{i - 2}$ ，故记录 $F_{i, 0}$ 表示 $f_{i}$ ， $F_{i, 1}$ 表示 $f_{i - 1}$ ，转移方程即

\begin{aligned} F_{i, 0} & = F_{i - 1, 0} + F_{i - 1, 1} \\ F_{i, 1} & = F_{i - 1, 0} \end{aligned}

注意到 $F_{i}$ 是 $F_{i - 1}$ 的 线性组合，因此

[\begin{matrix} F_{i - 1, 0} & F_{i - 1, 1} \end{matrix}] \times [\begin{matrix} 1 & 1 \\ 1 & 0 \end{matrix}] \to [\begin{matrix} F_{i, 0} & F_{i, 1} \end{matrix}]

这就是矩阵描述转移。

当转移系数如点权或边权带修时，重新 DP 的复杂度不可接受，考虑用数据结构如线段树维护 区间转移矩阵乘积 可支持单点修改。此方法还可快速计算一段区间或一棵子树的 DP 值，非常优美。DDP 也有局限性，它对转移方程要求较高。

说明：可以用矩阵描述的转移方程不一定必须是前驱的线性组合。广义矩阵乘法

C_{i, j} = ⨁_{k = 1}^{n} A_{i, k} \otimes B_{k, j}

只需满足 $⨂$ 具有 结合律，且 $⨂$ 对 $⨁$ 有 分配律，则存在结合律。设三个 $n$ 阶方阵 $A, B, C$ 相乘，有

\begin{aligned} ⨁_{q = 1}^{n} (A B)_{i, q} \times C_{q, j} \\ = & ⨁_{p = 1}^{n} (⨁_{q = 1}^{n} A_{i, p} \otimes B_{p, q}) \otimes C_{q, j} \\ = & ⨁_{p = 1}^{n} ⨁_{q = 1}^{n} A_{i, p} \otimes B_{p, q} \otimes C_{q, j} & (d i s t r i b u t i v e l a w) \\ = & ⨁_{p = 1}^{n} ⨁_{q = 1}^{n} A_{i, p} \otimes (B_{p, q} \otimes C_{q, j}) & (a s s o c i a t i v e l a w) \\ = & ⨁_{p = 1}^{n} A_{i, p} \otimes (⨁_{q = 1}^{n} B_{p, q} \otimes C_{q, j}) & (d i s t r i b u t i v e l a w) \\ = & ⨁_{p = 1}^{n} A_{i, p} \times (B C)_{p, j} \end{aligned}

常见广义矩阵乘法如 $min, +$ 卷积， $max, +$ 卷积，因为 $a + min (b, c) = min (a + b, a + c)$ ，即加法对 $min$ 有分配律。图论的邻接矩阵在 $or, and$ 卷积下的 $k$ 次方描述了每个点出发恰好走 $k$ 步到达的节点。

1.2 算法介绍：树链剖分写法

接下来，我们以 P4719 为例，深入剖析一下动态 DP 的一般树剖写法与诸多细节。

若没有修改操作，本题是经典的 树上最大独立集 问题，详见没有上司的舞会。设 $f_{i, 0 / 1}$ 分别表示不选或选点 $i$ 的最大权值，有

\begin{aligned} f_{i, 0} & = \sum_{x \in S_{i}} max (f_{x, 0}, f_{x, 1}) \\ f_{i, 1} & = v_{i} + \sum_{x \in S_{i}} f_{i, 0} \end{aligned}

加上修改操作，一般想法是用矩阵表示转移方程，再用数据结构维护。注意到一个节点可能有非常多的儿子，因此三方级别的矩阵乘法就凉了。

我们利用矩乘与 ds 能够 快速转移方程 的特点，与 树链剖分 从根到任意节点的轻边个数级别为 $O (\log)$ 的优秀性质，设计新的状态与转移方程。它应满足从一个点的 重儿子 转移到该点的方程可用矩阵描述。

首先，对树 $T$ 进行树链剖分，记 $s_{i}$ 为 $i$ 的重儿子。设 $g_{i, 0 / 1}$ 分别表示不选或选点 $i$ 且 只能从轻儿子 转移的最大权值，有

\begin{aligned} g_{i, 0} & = \sum_{u \in son (i) \land u \neq s_{i}} max (f_{u, 0}, f_{u, 1}) \\ g_{i, 1} & = v_{i} + \sum_{u \in son (i) \land u \neq s_{i}} f_{u, 0} \\ f_{i, 0} & = g_{i, 0} + max (f_{s_{i}, 0}, f_{s_{i}, 1}) \\ f_{i, 1} & = g_{i, 1} + f_{s_{i}, 0} \end{aligned}

定义广义矩阵乘法 $A \times B \to C$ 表示 $C_{i, j} = {max}_{k = 1}^{n} A_{i, k} + B_{k, j}$ 。由于 $max$ 对 $+$ 具有分配律： $max (a_{i} + b_{j}) = max a_{i} + max b_{j}$ ，而 $+$ 本身具有结合律，因此这样的矩阵乘法具有结合律，是优秀的。这样，我们有

[\begin{matrix} f_{s_{i}, 0} & f_{s_{i}, 1} \end{matrix}] \times [\begin{matrix} g_{i, 0} & g_{i, 1} \\ g_{i, 0} & - \infty \end{matrix}] \to [\begin{matrix} f_{i, 0} & f_{i, 1} \end{matrix}]

$f, g$ 需要 预处理（其实 $f$ 不需要，但是预处理 $g$ 依赖于 $f$ ）。记点 $i$ 从其重儿子转移上来的矩阵为 $G_{i}$ ，考虑支持修改操作：

我们注意到，一次修改仅改变 $O (\log)$ 级别个节点的 $G$ 。这是因为仅在 轻儿子被修改时 需要更新 $G$ ，而 $i \to R$ 的路径上只有 $O (\log)$ 条轻边。这样，我们不断跳重链，并实时维护每条 重链顶端节点 $t$ 的父节点 $f a_{t}$ 的 $G_{f a_{t}}$ 。

思考到这一步，我们遇到了所有 DDP 都需特别注意的关键问题：如何在修改点 $i$ 轻儿子的 $f$ 后维护该点的 $G_{i}$ 。注意到每个轻儿子对于父亲的 $G$ 的贡献以所有轻儿子的 $f$ 的和的形式计算，它满足 可减性，因此只需在修改前先计算原来的 $f$ ，将其贡献从 $g_{t p_{i}}$ 中减掉，再加上更新后的贡献即可。

如何求 $f$ ：注意到重链末端是叶子节点，而叶子节点没有 $s_{i}$ ，所以 $f_{i} = g_{i} (i \in leaf (T))$ 。因此一个点的 $f$ 等于 它所在重链末端到它的矩阵积。记录 $e d_{i}$ 表示 $i$ 所在重链末端叶子节点， $D_{i}$ 表示 $i$ 的 dfn， $f_{x}$ 可由 $\prod_{i = D_{x}}^{D_{e d_{x}}} G_{i}$ 。

上述过程要求我们在更新 $G_{i}$ 时先不要在线段树上修改，因为我们还需 原来的 $G_{i}$ 求出 $f_{t o p_{i}}$ ，以从 $G_{f a_{t o p_{i}}}$ 扣掉其贡献。这一要求体现在代码中即，设当前节点为 $x$ ，则将 $g_{f a_{t o p_{x}}}$ 减掉 $f_{t o p_{x}}$ 即从 $x$ 所在重链末端 $e d_{x}$ 一直到重链顶端 $t o p_{x}$ 的 $G$ 的乘积，在线段树上更新 $G_{x}$ ，再算出新的 $f_{t o p_{x}}$ 加到 $g_{f a_{t o p_{x}}}$ 上。

综上，时间复杂度线性对数平方，乘以矩阵乘法的时间，常数非常大。

const int N = 1e5 + 5;
const int inf = 1e9;

struct Matrix {
	int a, b, c, d;
	Matrix operator * (Matrix x) { // 广义矩阵乘法
		Matrix y;
		y.a = max(a + x.a, b + x.c);
		y.b = max(a + x.b, b + x.d);
		y.c = max(c + x.a, d + x.c);
		y.d = max(c + x.b, d + x.d);
		return y;
	}
} I, ans, G[N], val[N << 2];

int n, m, a[N], f[N][2], g[N][2];
int cnt, hd[N], nxt[N << 1], to[N << 1];
void add(int u, int v) {nxt[++cnt] = hd[u], hd[u] = cnt, to[cnt] = v;}
int dn, sz[N], fa[N], dep[N], son[N], dfn[N], rev[N], top[N], ed[N];
void GenMat(int x) {G[x].a = G[x].c = g[x][0], G[x].b = g[x][1], G[x].d = -inf;}

void dfs1(int id) {
	f[id][1] = a[id], sz[id] = 1, dep[id] = dep[fa[id]] + 1;
	for(int i = hd[id]; i; i = nxt[i]) {
		int it = to[i];
		if(it == fa[id]) continue;
		fa[it] = id, dfs1(it), sz[id] += sz[it];
		f[id][1] += f[it][0], f[id][0] += max(f[it][0], f[it][1]);  // 先处理出 f
		if(sz[it] > sz[son[id]]) son[id] = it;
	}
}
void dfs2(int id, int tp) {
	g[id][1] = a[id], top[id] = tp, rev[dfn[id] = ++dn] = id;
	if(son[id]) dfs2(son[id], tp), ed[id] = ed[son[id]];
	else ed[id] = id;
	for(int i = hd[id]; i; i = nxt[i]) {
		int it = to[i];
		if(it == fa[id] || it == son[id]) continue;
		dfs2(it, it), g[id][1] += f[it][0], g[id][0] += max(f[it][0], f[it][1]); // 再处理出 g
	}
}

struct SegTree {
	void build(int l, int r, int x) {
		if(l == r) return val[x] = G[rev[l]], void();
		int m = l + r >> 1;
		build(l, m, x << 1), build(m + 1, r, x << 1 | 1);
		val[x] = val[x << 1 | 1] * val[x << 1];
	}
	void modify(int l, int r, int p, int x) {
		if(l == r) return val[x] = G[rev[p]], void();
		int m = l + r >> 1;
		if(p <= m) modify(l, m, p, x << 1);
		else modify(m + 1, r, p, x << 1 | 1);
		val[x] = val[x << 1 | 1] * val[x << 1]; // 右乘左儿子
	}
	void query(int l, int r, int ql, int qr, int x) {
		if(ql <= l && r <= qr) return ans = ans * val[x], void();
		int m = l + r >> 1;
		if(m < qr) query(m + 1, r, ql, qr, x << 1 | 1); // 先递归右子树
		if(ql <= m) query(l, m, ql, qr, x << 1);
	}
} tr;

int modify(int x, int val) {
	g[x][1] += val - a[x], a[x] = val;
	while(top[x] != 1) {
		int tp = top[x], ft = fa[tp];
		ans = I, tr.query(1, n, dfn[tp], dfn[ed[tp]], 1);
		g[ft][1] -= ans.a, g[ft][0] -= max(ans.a, ans.b); // 先减掉 x 重链顶端父节点 ft 的 x 所在的轻儿子的 f 的贡献
		GenMat(x), tr.modify(1, n, dfn[x], 1); // update
		ans = I, tr.query(1, n, dfn[tp], dfn[ed[tp]], 1);
		g[ft][1] += ans.a, g[ft][0] += max(ans.a, ans.b), x = ft; // 再加回去
	} GenMat(x), tr.modify(1, n, dfn[x], 1);
	ans = I, tr.query(1, n, 1, dfn[ed[1]], 1);
	return max(ans.a, ans.b);
}
int main(){
	cin >> n >> m;
	for(int i = 1; i <= n; i++) a[i] = read();
	for(int i = 1, u, v; i < n; i++) add(u = read(), v = read()), add(v, u);
	dfs1(1), dfs2(1, 1);
	for(int i = 1; i <= n; i++) GenMat(i); tr.build(1, n, 1);
	for(int i = 1, x, y; i <= m; i++) x = read(), print(modify(x, read())), pc('\n');
	return flush(), 0;
}

注意点 1：由于 dfn 大的节点深度大，且转移顺序 自下而上，所以线段树维护时应用 右区间乘左区间，查询时也要先向右区间递归。这与写法习惯有关。用行向量右乘矩阵和用列向量左乘矩阵，线段树 push_up 时的区间顺序不同。总之，读者需要根据实际意义理解并实现。
注意点 2：就算初始全是单位矩阵 $I$ ，也要 初始化，因为大部分情况下 $I \neq [\begin{matrix} 0 & 0 \\ 0 & 0 \end{matrix}]$ 。
技巧 1：当矩阵乘法仅有某些位置上的值为非常数时，仅维护这些位置的值可以有效减小常数，如切树游戏。
技巧 2：一般情况下信息满足可减性，即直接从 $g_{f a_{i}}$ 中扣掉 $f_{i}$ 的贡献。不满足可减性时可以使用线段树维护带修半群元素积，但似乎如果没有可减性，我们甚至无法用矩阵描述转移，笔者也没有见过这样的题目。

1.3 全局平衡二叉树实现

等学会了 LCT 再来填坑。

upd：可能永远也不会填了，因为永远也不打算学 LCT。

1.4 例题

I. P4719 【模板】"动态 DP" & 动态树分治

动态 DP 的模板题。

II. CF750E New Year and Old Subsequence

题意简述：多次询问一个字符串的子串 $[l, r]$ ，求至少删去多少字符后才能使得其不包含子序列 $2016$ 而包含 $2017$ 。 $n, q \leq 2 \times 10^{5}$ 。

大力子序列自动机上 DP：设 $f_{i, 0 / 1 / 2 / 3 / 4}$ 分别表示包含 $\emptyset / 2 / 20 / 201 / 2017$ 且不包含 $2016$ 在 $[1, i]$ 中最少需要删去多少个字符，有：

{\begin{cases} f_{i, 0} = f_{i - 1, 0} + [s_{i} = 2] \\ f_{i, 1} = min (f_{i - 1, 1} + [s_{i} = 0], f_{i - 1, 0} [s_{i} = 2]) \\ f_{i, 2} = min (f_{i - 1, 2} + [s_{i} = 1], f_{i - 1, 1} [s_{i} = 0]) \\ f_{i, 3} = min (f_{i - 1, 3} + [s_{i} = 7 \lor s_{i} = 6], f_{i - 1, 2} [s_{i} = 1]) \\ f_{i, 4} = min (f_{i - 1, 4} + [s_{i} = 6], f_{i - 1, 3} [s_{i} = 7]) \end{cases}

对于直接接在 $f$ 后面而非 $+$ 后方的 $[]$ ，如果艾佛森括号中的条件不成立不能转移。由于转移维度非常小，仅有 $5$ ，故可将上式改写成 $min +$ 广义矩阵乘法形式。

每次询问用初始向量 $[\begin{matrix} 0 & \infty & \infty & \infty & \infty \end{matrix}]$ 乘 $[l, r]$ 用线段树维护的区间矩阵积，得到的 $f_{r, 4}$ 即为所求。若 $f_{r, 4} = \infty$ 则无解。

不难看出实际上 $\prod_{i = l}^{r} G_{i}$ 的第一行就是 $f_{r}$ ，其中 $G_{i}$ 是 $f_{i - 1} \to f_{i}$ 的转移矩阵，所以直接求出矩阵区间矩阵积也可。不过用向量乘矩阵 $f \times G$ 可以做到平方，而该方法 $G \times G$ 必须三方，常数较大。时间复杂度 $O (k^{2} (k n + q \log n))$ ，其中 $k$ 是转移维度，本题中为 $5$ 。

*III. P3781 [SDOI2017]切树游戏

题意简述：给出 $n$ 个节点的树，点有小于 $m = 2^{7}$ 的权值 $v_{i}$ ，权值带修。多次询问有多少非空子连通块满足所有点权值异或和为 $k$ 。 $n, q \leq 3 \times 10^{4}$ 。

首先设计 DP，设 $f_{i, x}$ 表示以 $i$ 为根的子树异或和为 $x$ 的方案数。合并 $u$ 及其儿子 $v$ 时，我们有转移方程

f_{u, j} \leftarrow f_{u, j} + \prod_{x \oplus y = j} f_{u, x} f_{v, y}

每个节点 $u$ 的初始值为 $f_{u, j} = [v_{u} = j]$ 。转移方程是异或卷积，两边同时取 FWT，得到 $F_{u} \leftarrow F_{u} (F_{v} + 1)$ 。这样， $O (n m \log m)$ 预处理每个节点的初始 FWT 值，单次对整棵树进行一遍树形 DP 的复杂度为 $O (n m)$ 。时间复杂度 $O (n m q)$ 。

考虑套上动态 DP，设 $g_{i, x}$ 表示从 $i$ 的 轻儿子 中选择若干个子树使异或和为 $x$ 的方案数，那么有转移方程

g_{u, j} \leftarrow g_{u, j} + \prod g_{u, x} f_{v, y} (v \neq heavy son (u))

由于我们要查询全树的 $\sum f_{i, x}$ ，所以还需记录 $h_{i, x}$ 表示 $\sum_{u \in subtree (i)} f_{u, x}$ ， $l h_{i, x}$ 表示 $\sum_{u \in lightson (i)} h_{u, x}$ 。设 $F_{i}, L F_{i}, H_{i}, L H_{i}$ 分别表示 $f_{i}, g_{i}, h_{i}, l h_{i}$ 的异或生成函数，有转移

\begin{aligned} F_{i} & = L F_{i} \times (F_{s_{i}} + x^{0}) \times x^{v_{i}} \\ L F_{i} & = x^{v_{i}} \times \prod_{u \in light son (i)} (F_{u} + x^{0}) \\ H_{i} & = L H_{i} + H_{s_{i}} + F_{i} \\ L H_{i} & = \sum_{u \in light son (i)} H_{u} \end{aligned}

[\begin{matrix} F_{s_{i}} & H_{s_{i}} & x^{0} \end{matrix}] \times [\begin{matrix} L F_{i} \times x^{v_{i}} & L F_{i} \times x^{v_{i}} & 0 \\ 0 & 1 & 0 \\ L F_{i} \times x^{v_{i}} & L H_{i} + L F_{i} \times x^{v_{i}} & 1 \end{matrix}] \Rightarrow [\begin{matrix} F_{i} & H_{i} & x^{0} \end{matrix}]

树剖线段树维护。修改需要实时更新 $L F$ 和 $L H$ ， $L H$ 可以直接减， $L F$ 需要维护乘以 $0$ 的个数与非零值之积，因为乘以 $0$ 时丢失了信息，不可逆。矩阵乘法的常数优化见基于变换合并的树上动态 DP 的链分治算法。视 $n, q$ 同阶，时间复杂度为 $O (n m \log^{2} n k^{3})$ ，其中 $k = 2$ 。

洛谷上树剖被卡了，必须使用全局平衡二叉树。LOJ 可以通过。

IV. P6573 [BalticOI 2017] Toll

究极套路题。注意到同一层大小仅有 $k$ 但层数很多，不难想到用矩阵描述每层之间的转移，用线段树支持查询，甚至不需要修改。用向量乘矩阵优化，时间复杂度 $O (n k^{3} + o k^{2} \log n)$ 。

V. P7359 「JZOI-1」旅行

裸题。不带修所以不需要线段树，直接倍增即可。时间复杂度 $O ((n + q) V^{3} \log n)$ ，其中 $V = 2$ 。

VI. LOJ #3539. 「JOI Open 2018」猫或狗

给定一棵 $n$ 个节点的树，节点有权值 $0 / 1 / 2$ 。带修权值并查询使所有权值为 $1$ 的点与权值为 $2$ 的点不连通最少需要割掉的边数。 $1 \leq n \leq 10^{5}$ 。

启示：连通性相关树上最优化问题考虑将连通性作为 DP 的维度。设 $f_{i, 0 / 1}$ 表示使 $i$ 不与 $1 / 2$ 连通的最小代价。转移显然：

f_{i, 0} = [v_{i} = 1] \times (+ \infty) + \sum_{j \in son (i)} min (f_{i, 0}, f_{i, 1} + 1)

对于 $f_{i, 1}$ 同理。带修点权考虑动态 DP，时间复杂度线性对数平方。细节：轻儿子对 $f$ 的贡献以和的形式计算，满足可减性，因此不需要线段树维护带修半群元素积。

2. 矩阵快速幂优化

2.1 算法简介

矩阵快速幂优化 DP 与动态 DP 的本质思想相同，都是用矩阵描述转移方程。不同的是，前者每一轮的转移方程相同，可以快速幂优化，后者则是套上各种数据结构支持修改。

仍然以斐波那契数列为例，因为每一轮转移的矩阵都是 $G = [\begin{matrix} 1 & 1 \\ 1 & 0 \end{matrix}]$ ，因此转移 $n$ 轮的矩阵就是 $G^{n}$ 。即 $[\begin{matrix} f_{i} & f_{i - 1} \end{matrix}] \times G^{n} \Rightarrow [\begin{matrix} f_{i + n} & f_{i + n - 1} \end{matrix}]$ 。由于矩阵乘法具有 结合律，因此可以快速幂优化，从而在对数时间内求解问题。

2.2 常见技巧

拆点：对于图上转移，当边权不为 $1$ 时，需要把每个点拆成 $w$ 个点， $w$ 是边权。因为 $f_{i, j}$ 会从 $f_{u, j - w}$ 转移，所以每个点要维护 $w$ 个时刻的信息。如例 VII. 和 VIII.
向量乘矩阵：对于多组矩阵快速幂询问且转移矩阵 $G$ 相同，我们预处理 $G$ 的 $2$ 的幂次方 $D_{i} = G^{2^{i}}$ 。我们知道向量乘矩阵可以做到平方，因此单次查询 $\vec{A} \times G^{i}$ 在快速幂过程中就不需要 $G$ 自乘，只需要向量乘矩阵，时间复杂度 $O (k^{2} (k + q) \log V)$ 。如例 VIII.
对于转移中存在的特殊时刻，可以配合技巧 2 做到特殊点数量 $\times k^{2} \log V$ 的时间复杂度，如例 VIII. 与 IX.。

2.3 例题

*I. P3176 [HAOI2015]数字串拆分

题意简述：定义 $f (s)$ 表示将 $s$ 拆分成若干个不大于 $m$ 个数的方案数。给出数字字符串 $t$ ，求 $g (t) = \sum f (x)$ ，其中 $x$ 为将 $t$ 分割成若干个允许有前导零的数后它们的和。例如 $t = 12$ 时，答案为 $f (1 + 2) + f (12)$ 。 $| s | \leq 500, m \leq 5$ 。

注意到 $m$ 的范围很小，仅有 $5$ ，所以 $f (s)$ 可以用矩阵快速幂 $m^{3} \log s$ 计算。记转移矩阵为 $G$ ，那么答案即为 ${(\sum_{x} G^{x})}_{0, 0}$ 。我们记 $D_{i}$ 表示 $g^{'} (t [1 : i]) = \sum G^{x}$ （注意区分 $g$ 和 $g^{'}$ ，前者是数值，后者是矩阵），则答案为 $(D_{n})_{0, 0}$ 。

不难写出转移方程 $D_{i} = \sum_{j = 0}^{i - 1} d_{j} \times f (t [j + 1 : i])$ 。因为 $t [j + 1 : i]$ 会很大，达到 $10^{n}$ 级别，所以快速幂的时候需要对指数高精：矩阵没有费马小定理！时间复杂度为 $O (n^{3} m^{3})$ ，无法承受。

注意到 $f (t) = G^{t} = \prod_{i = 1}^{| t |} G^{10^{| t | - i} t_{i}}$ （ $t$ 是字符串表示的十进制数， $t_{1}$ 为最高位），因此我们可以预处理出形如 $G^{c \times 10^{k}} (1 \leq c < 10, 0 \leq k < n)$ 的矩阵。记 $D_{l, r}$ 为 $f (t [l : r])$ ，它可以由 $D_{l + 1, r} \times G^{10^{r - l} t_{l}}$ 得到。

$n m^{3} | Σ | + n^{2} m^{3}$ 预处理后即可 $n^{2} m^{3}$ DP： $d_{i} = \sum_{j = 0}^{i - 1} d_{j} D_{j + 1, i}$ 。其中 $Σ$ 表示字符集即进制数，本题中为 $10$ 。

*II. CF576D Flights for Regular Customers

好题！将所有边按照 $d_{i}$ 排序并依次加入，并实时维护经过 $K$ 条边后能够到达的所有点。

设答案向量为 $A$ ， $A_{i} = 0 / 1$ 表示能否走到 $i$ 。有初始状态 $A_{1} = 1$ 。设当前走了 $K$ 步，先让 $A$ 乘以 $G$ 的 $d_{j} - K$ 次方，其中 $j$ 是下一条要加的边。加进去后，判断走 $d_{j}$ 步能到达的点到 $n$ 的最短距离 $D_{j}$ ，所有 $d_{j} + D_{j}$ 的最小值即为所求。因为尽管 $d_{j} < d_{j + 1}$ ，但并不一定满足 $d_{j} + D_{j} \leq d_{j + 1} + D_{j + 1}$ ，故不能在第一次连通时就认为找到答案。

根据或对与的分配律，使用矩阵快速幂解决。01 矩阵乘法用 bitset 优化，时间复杂度 $O (\frac{n m^{3} \log d}{ω})$ 。代码。

III. P1707 刷题比赛

有点裸，不过可以用来熟悉矩阵快速幂。

*IV. P4569 [BJWC2011]禁忌

题解。

V. P5059 中国象棋

注意到每一行是独立的，且方案数为 $f i b_{n + 3} - (n + 2)$ ：设 $f_{i}$ 表示第 $i$ 列（从 $1$ 下标开始，共有 $n + 1$ 列）不放棋子且任意两个不放棋子的格子间隔不超过 $2$ 的方案数，则有 $f_{0} = f_{1} = 1$ ， $f_{i} = f_{i - 1} + f_{i - 2}$ ，则 $f_{i} = f i b_{i + 1}$ 。总方案数为 $f_{n + 1} + f_{n} = f_{n + 2} = f i b_{n + 3}$ ，再减去全部不放的 $1$ 种和只有一个放的 $n + 1$ 种即可。故答案为 $(f i b_{n + 3} - n - 2)^{n + 1}$ 。矩阵快速幂计算 $f i b$ 。注意 $P \leq 10^{18}$ ，慢速乘。时间复杂度 $O (\log^{2} n)$ 。

VI. P1397 [NOI2013] 矩阵游戏

比较裸的矩阵加速 DP。我们没有办法快速十进制转二进制（复杂度 $\log^{2} n$ 直接爆炸），所以只能十进制预处理。时间复杂度 $O (\log_{10} n)$ ，有 $10 \times 2^{3} = 80$ 的常数。

VII. P3597 [POI2015]WYC

非常显然的矩阵快速幂，由于边权只有 $3$ 所以拆点：存储 $f_{i, j}, f_{i, j + 1}$ 和 $f_{i, j + 2}$ 表示以 $i$ 结尾的长度为 $j, j + 1, j + 2$ 的路径数量。最后再记一个 $s u m$ 表示路径总数，得到转移矩阵 $B$ 。预处理出 $B^{1}, B^{2}, \dots, B^{61}$ ，然后倍增求解即可。时间复杂度 $O (n^{3} \log k)$ ，有 $27$ 倍常数。注意矩阵每个数不可以取模，在任何时候都要对 $k$ 取 $min$ 。

*VIII. P6772 [NOI2020] 美食家

结合各种矩阵快速幂的常见优化技巧，拆点 + 预处理矩阵的 $2$ 的幂次方，容易做到 $O ((5 n)^{2} (5 n + k) \log T)$ ，复杂度与 $m$ 无关。

*IX. AT2371 [AGC013E] Placing Squares

考虑平方的组合意义实在是太神仙了，考虑维护 $g_{i, k} = \sum_{0 \leq j < i} f_{j} (i - j)^{k}$ ，其中 $f_{i}$ 表示 $[0, i]$ 的答案。转移把柿子写出来，用矩阵快速幂优化即可，注意要分标记点和非标记点讨论。时间复杂度 $m \times 3^{3} \times \log n$ 。

3. 状态压缩优化

状态压缩优化应用于以集合为状态的动态规划中。此时用 $0 / 1$ 表示某个元素是否在集合中，就可以用一个二进制数表示所有状态。

3.1 常见技巧

枚举子集：如果一个集合状态 $S$ 由其所有子集 $T ⊊ S$ 转移得到，这样转移的时间复杂度为 $\sum_{i = 0}^{n} (\binom{n}{i}) 2^{i} = 3^{n}$ 。代码实现形如：

for(int T = (S - 1) & S; ; T = (T - 1) & S) {
	......
	if(!T) break; 
}

进阶：高维前缀和（SOSDP）和子集卷积（Subset Convolution）本质上也是一种状压 DP。关于 SOSDP 详见位运算卷积，子集卷积与高维前缀和。

状压 DP 并没有一个很固定的模板，因此本质上仅是用二进制表示集合（或划分）的技巧，而非 DP 的优化方法。此外，状压 DP 是 插头 DP 的基础。

3.2 例题

高难度例题：II, VI, VII, VIII.

I. P1357 花园

注意到 $m, k$ 非常小而 $n$ 非常大，明示矩阵快速幂。首先考虑朴素 DP：状压，记 $f_{i, S}$ 为位置 $i$ 及其前 $m - 1$ 个位置所表示状态为 $S$ 时的方案数，转移枚举下一位是 C / P，判断合法性。

由于是环形 DP，所以枚举一开始 $m$ 个位置的状态 $S$ ，初始值 $f_{m, S} = 1$ ，那么 $s \leftarrow s + f_{n + m, S}$ 。总时间复杂度 $O (2^{m} \log n (2^{m})^{3}) = O (16^{m} \log n)$ 。

实际上最终答案可以由转移矩阵 $G$ 的 $n$ 次方的对角线求和得到： $f_{m, S}$ 对 $f_{n + m, S}$ 有贡献。复杂度降至 $O (8^{m} \log n)$ 。

*II. AT695 マス目

题解。

*III. ACM/ICPC Regional Aizu 2013 Hidden Tree

注意到一棵 balanced tree 上所有数都是最小数乘以 $2$ 的幂，因此，对于不同的 $p \times 2^{r} (2 ∤ p)$ 我们单独处理。

计算每个数中有多少个质因子 $2$ ，记做 $r$ ，状压 $f_{i}$ 表示当前所有数的和为 $i$ 时，最多的叶节点个数。按位置顺序枚举所有 $2^{r}$ ，并令 $f_{k + 2^{r}} \leftarrow max (f_{k + 2^{r}}, f_{k} + 1) (2^{r} ∣ k)$ 。

后面的条件是因为加入 $2^{r}$ 之后其后面比 $2^{r}$ 小的部分就没法跨过 $2^{r}$ 和前面比 $2^{r}$ 小的部分互相抵消。记 $c = ⌊ \log_{2} n ⌋ + max r$ ，最大约为 $8 + 9 = 17$ ，则时间复杂度为 $O (T n 2^{c})$ 。

IV. 2021 联考模拟北大附瘟疫公司

给出一张 $n$ 个点有边权的无向图。定义点集 $S$ 的代价 $c_{S}$ 为连通这些点的最小代价和最大代价异或和。试确定一个点集序列 $S_{1} \subset S_{2} \subset \dots \subset S_{k}$ 满足 $S_{1}$ 包含 $1$ 个点且 $S_{k}$ 包含所有点，最小化 $\sum_{i = 2}^{k} | S_{i} ∖ S_{i - 1} | \times c_{S_{i}}$ 。 $n \leq 20$ ， $m \leq 100$ 。

首先 kruskal $2^{n} (n \log n + m)$ 求出每个点集 $S$ 的代价 $c_{S}$ ，我们有显然的状态设计 $f_{S}$ 表示扩展为 $S$ 的最小代价。朴素暴力是 $f_{S} = min_{T \subset S} f_{T} + c_{S} \times | S ∖ T |$ ，直接计算的复杂度是 $O (3^{n})$ 。但注意到一个关键性质：我们只关心 $T$ 的大小而非具体包含了哪些元素，这启发我们修改状态设计 $g_{i, S}$ 表示 $S$ 大小为 $i$ 的子集 $T$ 的 $min f_{T}$ 。转移即

g_{i, S} = {\begin{cases} min_{p \in S} g_{i, S ∖ p} & i < | S | \\ min_{0 \leq j < | S |} g_{j, S} + c_{S} \times (i - j) & i = | S | \end{cases}

时间复杂度 $O (2^{n} (n^{2} + m))$ 。

启示：DP 状态的设计时尽量 忽略无用信息，抓住 对转移有关键影响的量。思路：求出代价 $\to$ 设计朴素暴力 $\to$ 发现只有子集大小有关 $\to$ 将子集大小加入 DP 状态。

V. P5911 [POI2004]PRZ

状压枚举子集，时间复杂度 $O (3^{n})$ 。

*VI. CF1463F Max Correct Set

考虑问题的弱化版本。当 $x = y$ 时，我们可以构造出一组最优解 $11 \dots 1100 \dots 0011 \dots$ ，即 $x$ 个 $1$ 和 $x$ 个 $0$ 打包在一起。

因此，对于更一般的情况，我们猜测最优解存在循环节 $x + y$ 。对于前 $min (n, x + y)$ 个位置做状压 DP，时间复杂度 $O (2^{max (x, y)} (x + y))$ 。证明略。代码。

*VII. CF1152F2 Neko Rules the Catniverse (Large Version)

神仙题。按位置的顺序 DP 显然行不太通，注意到对于所有相邻位置均有值域上的限制，因此考虑 按值域从小到大 DP。

不妨设当前值为 $i$ ，考虑要知道哪些信息才能转移。首根据长度限制 $k$ ，我们得及时终止，所以要知道序列里已经放了多少个数。记录 $j$ 表示序列长度为 $j$ 。根据值域限制，只有权值 $\geq i - m$ 的位置之后或序列的开头才能放。因此，为求出将 $i$ 放入序列的方案数，记录 $S$ 表示 $\geq i - m$ 的权值有哪些在序列中，这是一个状压形式的维度。

转移就很简单了，方案数作为系数直接乘上去：

\begin{aligned} f_{i, j, S} \times (popcount (S) + 1) & \to f_{i + 1, j + 1, (2 S + 1) & (2^{m} - 1)} (i < n \land j < k) \\ f_{i, j, S} & \to f_{i + 1, j + 1, (2 S) & (2^{m} - 1)} (i < n) \end{aligned}

由于 $n$ 很大，所以直接 DP 不太行。但是 $k \times 2^{m}$ 很小，所以直接矩阵快速幂即可。时间复杂度 $O (k^{3} 8^{m} \log n)$ 。代码。

*VIII. CF1342F Make It Ascending

题目相当于求将序列 $a$ 划分为若干集合 $S_{1}, S_{2}, \dots S_{c}$ ，集合之间有序，满足 $S_{i}$ 之和小于 $S_{i + 1}$ 之和（单调递增），且存在一个单调上升序列 $p$ 满足 $p_{i} \in S_{i}$ ，即我们最终会将 $S_{i}$ 所有其它元素累和到原序列位置为 $p_{i}$ 的元素上。求最多划分出多少集合。

朴素的想法是将所有限制全部装进 DP 里面，即设 $f_{i, j, k}$ 表示当前考虑了 mask 为 $i$ 的数集，最后一个划分出的集合对应的 $p$ 的最小值为 $j$ ，且总和为 $k$ 时，最多划分出多少集合。转移根据实际意义显然。

这样复杂度太大了，因为我们把值域装了进去。考虑如何把值域去掉。由于若 $k > k^{'}$ 且 $f_{i, j, k} \leq f_{i, j, k^{'}}$ ，则前者显然无用。这说明 对于相同的 $f_{i, j, k}$ ，仅有最小的 $k$ 有用。根据这一性质，我们尝试 忽略无用状态，交换 DP 的某一维度和值域。这意味着，我们设 $f_{i, j, k}$ 表示当处于上述意义下的 $i, j$ 以及 集合个数 为 $k$ 时，最后一个集合的和的最小值。转移即在 $i$ 这一维枚举子集，同时枚举 $j, k$ 。

转移条件有三个：

$\sum_{p \in S} a_{p} > f_{i, j, k}$ 。
存在 $p \in S$ 使得 $p > j$ 。设 $p_{min}$ 为最小的这样的 $p$ 。
$i \cap S = \emptyset$ 。

则 $f_{i, j, k}$ 可以转移到 $f_{i \cup S, p_{min}, k + 1}$ ，并令后者对 $\sum_{p \in S} a_{p}$ 取最小值。容易发现时间复杂度为 $O (3^{n} n^{2})$ 。由于不合法状态较多，跑不满（若 $f_{i, j, k}$ 为 $\infty$ 则不用枚举 $i$ 的补集的子集），时限非常大，故可以通过。代码。

4. 单调队列优化： $t$ D / $e$ D

单调队列优化常见于 任何维度 的动态规划。可见它是多么基础。

4.1 算法简介

“当一个选手比你小还比你强，你就打不过他了”。这是对单调队列非常形象的概括。

具体地，单调队列通过 及时排除不可能成为最优转移的位置，将寻找决策点的复杂度均摊成 $O (1)$ ，从而保证时间复杂度。能够单调队列优化的转移方程一般可写成：

f_{i} = max_{j \in [l_{i}, i - 1]} f_{j} + A_{j} + B_{i}

其中 $A_{j}$ 是 仅与 $j$ 有关 的变量， $B_{i}$ 是 仅与 $i$ 有关 的变量，同时还需满足可行决策左端点 $l_{i}$ 随着 $i$ 增加而单调不降。不难发现我们要求 $f_{i} + A_{i}$ 的最大值，其本质就是 滑动窗口：在将元素 $f_{i}$ 加入队列 $Q$ 时，若 $f_{t} + A_{t} \leq f_{i} + A_{i}$ 说明 $t$ 一定不优于 $i$ ，不断弹出队尾直到队列为空或 $f_{t} + A_{t} > f_{i} + A_{i}$ 。同时，在转移时若队首位置 $h < l_{i}$ 说明 $h$ 已经过时，不断弹出队首直到 $h \geq l_{i}$ 。弹出 $h$ 使得队列为空的情况在大部分题目中不会发生，因为 $i - 1 \in Q$ 。部分题目则需要特判。

经过上述操作后，取出队首 $h$ ，它一定满足 $h \in [l_{i}, i - 1]$ 且 $f_{h} + A_{h}$ 在所有 $[l_{i}, i - 1]$ 的下标中最大，否则它要么作为队首弹出，要么被某个更大的 $f + A$ 弹出。因此 $h$ 就是 $i$ 的决策点。

4.2 常见技巧

一般的转移方程并不友好，因为贡献 $v a l$ 常常与 $i, j$ 同时有关。此时可尝试将 $v a l$ 拆开，写成 $v a l = A_{j} + B_{i}$ 的形式，如当 $v a l = j - i$ 时， $A_{j} = j$ ， $B_{i} = - i$ ，因此将 $f_{j} + j$ 而非 $f_{j}$ 加入单调队列可保证正确性。

结合下方应用以更好理解。

4.3 应用：单调队列优化多重背包

记物品个数为 $n$ ，背包容量为 $V$ 。第 $i$ 个物品体积为 $V_{i}$ ，价值为 $v a l_{i}$ 且最多放 $c_{i}$ 个。设 $f_{i, j}$ 为前 $i$ 个物品体积之和为 $j$ 的最大价值，暴力显然有

f_{i, j} = max_{0 \leq k \leq c_{i} \land k V_{i} \leq j} f_{i - 1, j - k V_{i}} + k \times v a l_{i}

考虑 拆贡献：考察每个 $f_{i - 1, j^{'}}$ 对 $f_{i, j} (j^{'} \leq j \land V_{i} ∣ j - j^{'})$ 的贡献：记 $k = \frac{j - j^{'}}{V_{i}}$ ，那么 $0 \leq k \leq c_{i}$ ， $f_{i - 1, j^{'}} + k \times v a l_{i} \to f_{i, j}$ 。注意到 $k$ 与 $j, j^{'}$ 同时有关，那么在 $i$ 固定时，对于每个相差 $V_{i}$ 的 $j$ ，相同的合法的 $j^{'}$ 的贡献不一样。

注意到当 $j$ 增加 $V_{i}$ 时，对于相同的 $j^{'}$ ，其 $k$ 值就会增加 $1$ 。遇到这样的情况，我们会在 $j^{'}$ 处减去一定的关于 $j^{'}$ 的贡献，并在 $j$ 处增加一定的关于 $j$ 的贡献。这本质上是将 $k$ 看做 $⌊ \frac{j}{V_{i}} ⌋ - ⌊ \frac{j^{'}}{V_{i}} ⌋$ 。改写上式：记 $j = q V_{i} + r (0 \leq r < V_{i})$ ，则

f_{i, j} = q \times v a l_{i} + {max}_{k = 0}^{min (c_{i}, q)} f_{i - 1, j - k V_{i}} - (q - k) \times v a l_{i}

这很好理解，因为上式的 $q$ 就是 $⌊ \frac{j}{V_{i}} ⌋$ ，而我们尝试枚举 $k$ ，因此 $j^{'}$ 对应的 $q^{'} = ⌊ \frac{j^{'}}{V_{i}} ⌋ = ⌊ \frac{j}{V_{i}} ⌋ - k = q - k$ 。它是一个仅与 $j^{'}$ 有关的量。

因为对于相同的 $j^{'}$ ， $q^{'} = q - k$ 的值是定值，为 $⌊ \frac{j^{'}}{V_{i}} ⌋$ ，同时 $q \times v a l_{i}$ 是一个只关于 $j$ 的值，所以可以用单调队列优化区间 $max$ 。实际上，这就是将 $j^{'} \to j$ 的贡献减去了 $\frac{j^{'}}{V_{i}}$ ，并将 $j$ 自身的贡献增加了 $\frac{j}{V_{i}}$ 。这并不改变 $j^{'} \to j$ 的贡献，因为 $k = \frac{j - j^{'}}{V_{i}}$ 。例题如 III.

4.4 例题

I. *P2254 [NOI2005] 瑰丽华尔兹

注意到求最长滑行距离等价于求最少使用魔法的次数，那么设 $f_{t, i, j}$ 表示 $t$ 时间使钢琴在 $(i, j)$ 的最少魔法使用次数。 $O (n m t)$ 无法承受。

注意到一段时间内移动方向相同，设 $f_{k, i, j}$ 表示在第 $k$ 段结束后使钢琴在 $(i, j)$ 的最少魔法使用次数。以向右移动为例：设持续时间为 $L = t_{k} - s_{k} + 1$ ，则：

f_{k, i, j} = {min}_{p = max (0, j - l a s)}^{j} f_{k - 1, i, p} + L - (j - p)

并满足 $(i, p), (i, p + 1), \dots, (i, j)$ 之间没有障碍。使用常见的拆贡献套路，将 $L - (j - p)$ 拆成 $p$ 和 $L - j$ ，这样贡献就分别与 $p, j$ 有关，可以使用单调队列优化。其余方向同理，时间复杂度为 $O (n m k)$ 。

II. P3572 [POI2014]PTA-Little Bird

f_{i} = {min}_{j = i - k}^{i - 1} f_{j} + [d_{j} \leq d_{i}]

由于 $d_{j} \leq d_{i}$ 的贡献仅有 $1$ ，因此将 $i$ 压入队列和队尾 $t$ 比较时，若 $f_{i} < f_{t}$ 或 $f_{i} = f_{t} \land d_{i} \geq d_{t}$ ，说明 $i$ 不劣于 $t$ ：当 $f_{i} < f_{t}$ 时，显然有 $f_{i} + [d_{i} \leq d_{i^{'}}] \leq f_{t} + [d_{t} \leq d_{i^{'}}]$ 。时间复杂度 $O (n q)$ 。

III. P3423 [POI2005]BAN-Bank Notes

单调队列优化多重背包模板题。由于要记录转移点，时空复杂度均为 $O (n k)$ 。

IV. P3487 [POI2009]ARC-Architects

POI 真的很喜欢出单调队列！

字典序最大给予我们贪心的思路，即优先选择最大的数字肯定更优，若数字相同则尽量选更前面的，因为这样剩下来的选择就更多。如 $[9, 7, 9, 6]$ ，选前面的 $9$ 就比选后面的 $9$ 好。

但是有 $b_{i} < b_{i + 1}$ 的限制，说明如果我们选最大的，可能导致后面没法选了。因此不妨设我们在选 $b_{i}$ ，我们只能从下标为 $[b_{i - 1} + 1, k - i + 1]$ 的数当中挑选，因为如果 $b_{i}$ 再大一点，那么无论如何我们都选不齐 $k$ 个数。实现就是经典滑动窗口，若当前数等于单调队列队尾则不弹出，保证了相同数优先选择更前面的。时间复杂度线性。

V. P3512 [POI2010]PIL-Pilots

POI 真的很喜欢出单调队列！直接 two-pointers + 两个单调队列就做完了。时间复杂度线性。

VI. P3422 [POI2005]LOT-A Journey to Mars

POI 真的很喜欢出单调队列！一开始看错题，以为可以来回走，以为是个神题，想了两个小时 ……

首先破环成链，考虑从 $i$ 开始顺时针方向 $i \to i + 1 \to i + 2 \to \dots \to i + n - 1 \to i + n$ 能不能走到，也就是要满足 $p_{i} \geq d_{i}$ ， $p_{i} + p_{i + 1} \geq d_{i} + d_{i + 1}$ …… 前缀和 优化一下即对于每个 $k \in [i, i + n - 1]$ ，都要有 $p_{k} - p_{i - 1} \geq d_{k} - d_{i - 1}$ ，稍做变形得到 $p_{i - 1} - d_{i - 1} \leq min_{i \leq k < i + n} p_{i - 1} - d_{i - 1}$ ，经典的滑动窗口。

对于逆时针方向，同理要有 $d_{i - 1} - p_{i} \leq min_{i - n \leq k < i} d_{k - 1} - p_{k}$ （手动模拟一下容易得到），也是滑动窗口。时间复杂度线性。

*5. wqs 二分优化：2D / 1D

王钦石二分，简称 wqs 二分，又称带权二分，斜率凸优化。常与斜率优化（例题 IX $\sim$ XII. 详见 Part 7），二分队列（Part 8）等方法结合使用。

该算法常见于 限制选取物品个数 的 DP。它有很明显的标志，因此看起来比较套路。

设 $f (i)$ 表示最多（或恰好，或至少）选取 $i$ 个物品时的答案，若 $f$ 为凸函数则适用 wqs 二分。通常 $f$ 的凸性难以证明，考场上可以猜结论： $n k$ 做不了就是凸的。

常见证明凸性的方法：

考虑选取 $i - 1$ 和 $i + 1$ 个物品的最优方案，调整得到选取 $i$ 个物品的方案，同时证明 $f (i)$ 不大于或不小于 $\frac{f (i - 1) + f (i + 1)}{2}$ 。
将问题抽象成费用流模型，则每一滴流量带来的贡献单调不减或单调不增。

不妨设 $f (i)$ 下凸，即 $f (i) - f (i - 1)$ 随着 $i$ 增大而增大。我们将 $f$ 形成的凸包画出来：

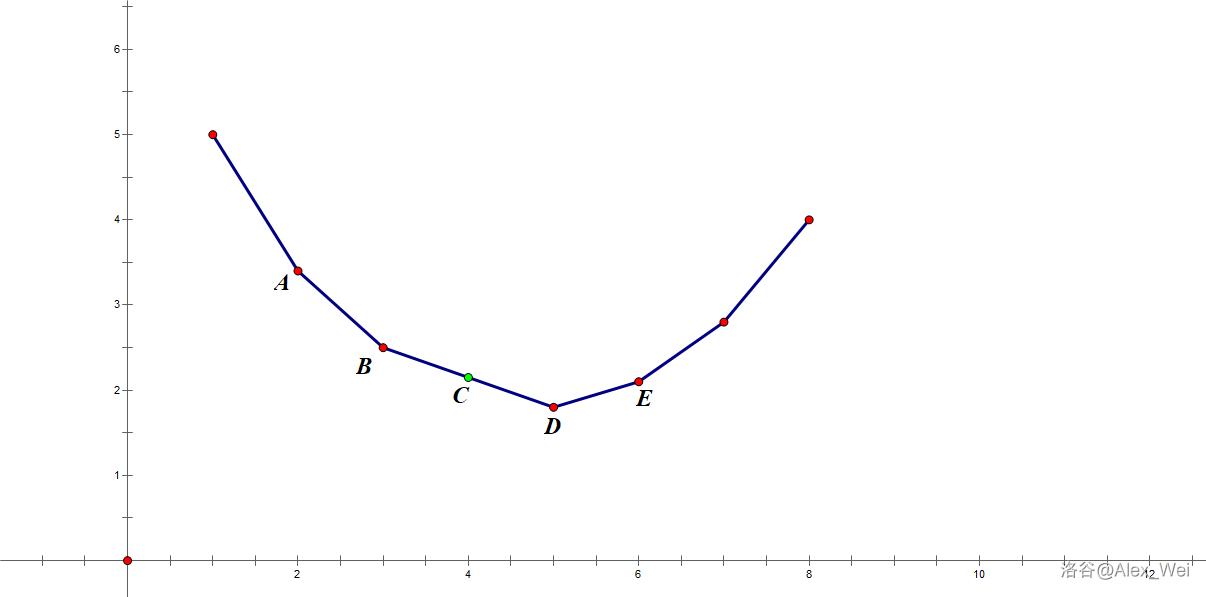
其中用绿色标出的点为 $(m, f (m))$ 。

考虑用斜率 $k$ 的直线 $l_{k}$ 截凸包，则对于点 $(i, f (i))$ ，其在 $y$ 轴上的截距为 $f (i) - k i$ 。如果我们可以求出 $l_{k}$ 截到的点的横坐标 $p$ 及其在 $y$ 轴上的截距 $b_{k}$ ，则根据 $b_{k} = f (p) - k p$ 可知 $f (p) = b_{k} + k p$ 。因此，我们希望 $p = m$ 。这样已知 $k$ 和 $b_{k}$ ，可得 $f (m) = b_{m} + k m$ 。

通过比较 $p$ 和 $m$ 的大小可知 $k$ 偏大还是偏小。若 $p < m$ 说明斜率偏小，应当更大；若 $p = m$ 说明已经找到答案；若 $p > m$ 说明斜率偏大，应当更小。注意，当 $f$ 上凸时大小关系会反转，读者应当根据实际意义理解。这样，通过二分可在 $\log V$ 次给定斜率 $k$ 求切点的操作后求得 $f (m)$ 。

问题转化为求切点。用 $l_{k}$ 切下凸包，可知截距为 $f (p) - k p$ 的最小值，对应横坐标即取到最小值的 $p$ 。换言之，我们希望求出 ${min}_{p = 1}^{n} f (p) - k p$ 以及对应的 $argmin$ 。

进行一步非常巧妙的转化：我们发现 ${min}_{p = 1}^{n} f (p) - k p$ 即原问题在 每选一个物品有 $- k$ 的代价 且 不限段数 的情况下的最小代价。因为原问题可用 2D / 1D DP 解决，所以去掉一维物品个数后，用 1D / 1D DP 解决转化后的问题，同时记录 选取物品个数 以求出切点横坐标。得到截距 $b_{k}$ 和切点横坐标 $p$ 后容易根据斜率 $k$ 算出切点纵坐标 $f (p) = b_{k} + k p$ 。

时间复杂度为 $O (c \log V)$ ，其中 $c$ 为一次内层 DP 复杂度，通常 $c$ 等于 $O (n)$ 或 $O (n \log n)$ 。

5.2 细节：数据类型

大部分题目 $f (i)$ 为整数，所以斜率 $\frac{f (i + 1) - f (i)}{i + 1 - i} = f (i + 1) - f (i)$ 为整数，因此王钦石二分斜率 $k$ 为整数。

部分题目涉及小数运算，斜率不是整数。这种情况建议平衡精度与效率，设定二分次数 $- \log ϵ$ ，并在找到解 $p = m$ 时结束王钦石二分。

5.3 特殊情况：三点共线

三点共线是王钦石二分最重要也最容易出错的细节之一。

三点共线可能导致我们无论如何也二分不到想要的 $k$ 。即斜率为 $k$ 时 $p < m$ ，斜率为 $k^{'} = k + 1$ 或 $k - 1$ 时 $p^{'} > m$ 。

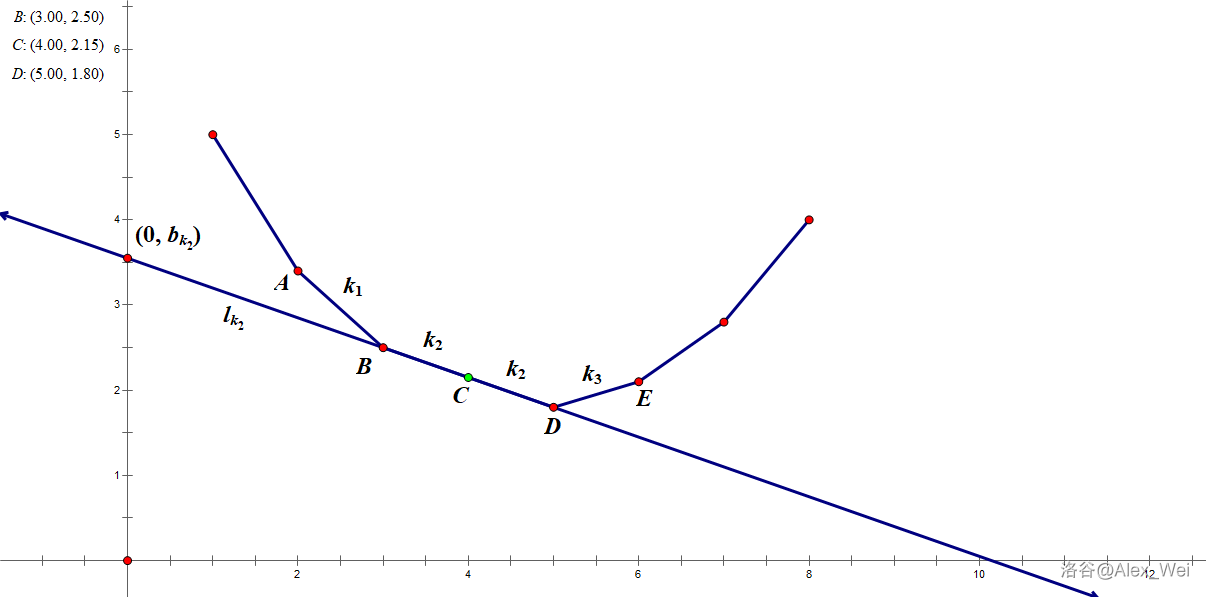
如图，设 $m = x_{C}$ 。若二分得到斜率 $k_{2}$ ，则无论切到的是点 $B$ ， $C$ 还是 $D$ ，斜率为 $k_{2}$ 时它们在 $y$ 轴的截距 $b_{k_{2}}$ 相同，所以算出来的 $f (m) = b_{k_{2}} + k_{2} m$ 也相同，不影响最终答案。

有一点需要格外注意：

如果在保证答案最优的前提下求得段数最大值，那么当 $p < m$ 时应有 $l \leftarrow m i d + 1$ ， $p > m$ 时应有 $r \leftarrow m i d$ 。
- $k = k_{1}$ 时截到点 B，因为 $x_{B} < x_{C}$ ，所以 $k_{1}$ 一定不是 我们要找的斜率， $l \leftarrow m i d + 1$ 。
- $k = k_{2}$ 时截到点 D，因为 $x_{D} > x_{C}$ ，所以 $k_{2}$ 可能是 我们要找的斜率， $r \leftarrow m i d$ 。
- 所以 $m i d$ 应为 $⌊ \frac{l + r}{2} ⌋$ 。
相反，如果求得段数最小值，那么当 $p < m$ 时应有 $l \leftarrow m i d$ ， $p > m$ 时应有 $r \leftarrow m i d - 1$ 。
- $k = k_{3}$ 时截到的点是 D，因为 $x_{D} > x_{C}$ ，所以 $k_{3}$ 一定不是 我们要找的斜率， $r \leftarrow m i d - 1$ 。
- $k = k_{2}$ 时截到的点是 B，因为 $x_{B} < x_{C}$ ，所以 $k_{2}$ 可能是 我们要找的斜率， $l \leftarrow m i d$ 。
- 所以 $m i d$ 应为 $⌊ \frac{l + r}{2} ⌋ + 1$ 。

对比上述两种情况，可知在保证答案最优的前提下，求物品个数 最大值 或 最小值 对二分过程有很大影响。

注意：上述结论的前提为 $f$ 下凸。 $f$ 上凸时可类似讨论。

易错点：注意，若二分求得斜率 $k$ ，切点横坐标 $p$ 及其截距 $b_{k}$ ，则答案为 $b_{k} + k m$ 而非 $b_{k} + k p$ 。这是初学者常见错误。根据实际意义理解， $b_{k} + k p$ 是 $f (p)$ 而不是要求的 $f (m)$ 。

5.4 细节：更新答案

若边界值变为 $m i d$ 则更新答案，直接给答案赋值 而不是取 $min / max$ 。相反，若边界值变为 $m i d \pm 1$ 则不更新，因为 $m i d$ 处的答案 没有被取到。

如果答案所对应的斜率没有被 DP 过怎么办？实际上不会出现这种情况。类比普通二分能二分出边界值，wqs 二分也能二分出边界斜率。

5.5. 技巧

wqs 二分的常用技巧：用结构体将 DP 值与所选取物品个数结合在一起，不仅方便更新 DP 值，还能快速比较两个 DP 值的偏序关系：根据 5.3 所述细节，若 DP 值相同还需根据所选取的物品个数钦定大小关系。重载运算符可以做到。具体实现见例题 III.

5.6 参考博客

在此感谢这些博主。

5.7 例题

很多时候我们都猜测答案是凸函数，而非严谨证明。

I. P2619 [国家集训队] Tree I

本题是 wqs 二分的经典题。但在这里的用途并不是优化 DP。

设 $f_{i}$ 表示恰好选取 $i$ 条白边时的答案，感性猜测 $f_{i}$ 是关于 $i$ 的下凸函数，使用 wqs 二分即可。

II. CF739E Gosha is hunting

$n^{3}$ 的 DP 显然：设 $f_{i, j, k}$ 表示考虑了前 $i$ 个神奇宝贝，用了 $j$ 个宝贝球和 $k$ 个超级球时期望最大个数。猜测答案 $F (a, b)$ 关于 $a, b$ 都上凸，因此对其中一维使用 wqs 二分，时间复杂度平方对数。

更进一步地，两维上都具有凸性使得我们可以二分套二分做到线性对数平方。代码。

*III. P4383 [八省联考2018]林克卡特树

神仙题，顺便巩固一下树形 DP。题目本质是选择恰好 $K + 1$ 条树上不相交简单路径，求最大权值。猜测它可以 wqs 二分，实际上确实可以（不然就没法做了）。

尝试设计在 wqs 二分内部的树形 DP。单走一个 $f$ ，发现做不了，我们只好多记录一些状态：由于一个节点 度数不超过 $2$ ，因此设 $f_{i, j} (j \in [0, 2])$ 表示在以 $i$ 为根的子树中，节点 $i$ 的度数为 $j$ 时的答案，且 $j = 1$ 时与 $i$ 相连的链不计入链的总数，所减去的斜率也不算。这是 记录路径延伸情况 的常见套路。

另外记录当前 DP 值下链的条数的 最大值 方便判断 wqs 二分截得的点的横坐标。记 $g_{i} = max (f_{i, 0}, f_{i, 1} - k, f_{i, 2})$ ，设当前合并 $i$ 与其儿子 $u$ ，有转移方程：

\begin{aligned} f_{i, 0} = max (f_{i, 0}, f_{i, 0} + g_{u}) \\ f_{i, 1} = max (f_{i, 1}, f_{i, 0} + f_{u, 1} + w_{i, u}, f_{i, 1} + g_{u}) \\ f_{i, 2} = max (f_{i, 2}, f_{i, 1} + f_{u, 1} + w_{i, u} - k, f_{i, 2} + g_{u}) \end{aligned}

不难发现 $g_{j}$ 表示以 $j$ 为根的子树中，与 $j$ 的父亲不连边时的答案，而 $f_{i, 1} - k$ 相当于在 $i$ 处直接把链掐断了。因此 $g_{1}$ 即为所求。

注意点：计算 $f_{i, 1}$ 时链的总数及其减去的贡献 $k$ 一定要留着最后形成一条链时计算，否则会使答案错误。此外，同一层 $i, u$ 内的转移顺序应该是 $f_{i, 2}, f_{i, 1}, f_{i, 0}$ ，观察一下转移方程就能知道原因。时间复杂度线性对数。代码。

*IV. CF802O April Fools' Problem (hard)

神仙题！双倍经验：CF802N April Fools' Problem (medium)。

这个题神仙之处在于如何对贪心进行反悔： $f (i)$ 下凸，且斜率不可能为负数，因此二分斜率在 $[0, 2 \times 10^{9}]$ 之间。

接下来考虑怎么贪心：对于每一个 $b_{i}$ 找到在它之前没有被选过的 $a_{j}$ ，若 $a_{j} + b_{i} - k \leq 0$ 则选择 $a_{j}$ 并将答案加上 $a_{j} + b_{i} - k$ 。但是这样是错的，如 $k = 5$ ， $a = {1, 233}$ ， $b = {3, 1}$ ，我们会将 $b_{1}$ 和 $a_{1}$ 匹配，但是 $b_{2} + a_{1} - k$ 更小。

考虑如何反悔：每个 $b_{i}$ 要么不选，要么和 $a_{j}$ 匹配，贡献为 $a_{j} + b_{i} - k$ 。要么把某一个 $b_{j}$ 顶替掉，贡献为 $b_{i} - b_{j}$ 。将 $b_{i}$ 提出，发现我们要找的就是 $a_{j} - k$ 和 $- b_{j}$ 的最小值，用堆维护即可。注意还需记录堆中的每个数形如 $a_{j} - k$ 还是 $- b_{j}$ ，从而计算打印好的题目数量。时间复杂度线性对数平方，代码非常短。

V. P1484 种树

注意题目求的是最多 $k$ 个，所以斜率下界从 $0$ 开始。这样可以保证二分出来的点一定不在 $k$ 右边且 $f_{1}$ 到 $f_{p}$ 单调不降，即 $f_{p}$ 为 $f_{1} \sim f_{k}$ 的峰值。若斜率从负数开始，我们二分得到的 $f_{k}$ 不一定是最优解，因为可能 $f_{k - 1} > f_{k}$ ：权值有负数。

时间复杂度线性对数，关于本题的反悔贪心解法见例题 VII. 给出的链接。

VI. P1792 [国家集训队]种树

双倍经验。显然如果 $n < 2 k$ 则无解。否则破环成链，从 $1$ 和 $2$ 开始分别 DP 一遍，最终 DP 结果即第一次的 $g_{n - 1}$ 和第二次的 $g_{n}$ 的最大值。时间复杂度同上题。

VII. P3620 [APIO/CTSC 2007]数据备份

三倍经验。相邻两个坐标相减，即求不相邻的 $k$ 个数之和的最小值，wqs 二分即可。时间复杂度同上题。本题的贪心做法详见贪心专题。

四倍经验：SP1553 BACKUP - Backup Files。

VIII. CF958E2 Guard Duty (medium)

五倍经验。

*IX. P5896 [IOI2016] aliens

题解。

*X. P5308 [COCI2019] Quiz

猜想答案关于 $k$ 是上凸函数，wqs 二分去掉 $k$ 的限制。设 $f_{i}$ 表示剩下 $i$ 个人时的最大收益，有 $f_{i} = max_{i < j \leq n} f_{j} + \frac{j - i}{j}$ 。显然的斜率优化。时间复杂度 $O (w n)$ ，其中 $w$ 是设置的二分次数。

XI. P4072 [SDOI2016]征途

注意到题目限制恰好 $m$ 天，猜想最优答案是关于 $m$ 的下凸函数，果断 wqs 二分。设 $s_{i}$ 为路程长度前缀和， $d = \frac{s_{n}}{m}$ ，方差式子乘上 $m^{2}$ 就是 $m [(l_{1} - d)^{2} + (l_{2} - d)^{2} + \dots + (l_{m} - d)^{2}]$ ，其中 $l_{i}$ 是每一段路程长度。化简即 $\sum m (l_{i}^{2} - 2 l_{i} d + d^{2})$ ， $m$ 个 $d^{2}$ 提出来，乘个 $m$ 再合并同类项就是 $- s_{n}^{2} + \sum m l_{i}^{2}$ 。

求后一项的最小值可以斜率优化： $f_{i} = {min}_{j = 0}^{i - 1} f_{j} + m (s_{i} - s_{j})^{2}$ 。时间复杂度线性对数，非常优秀。

XII. P4983 忘情

发现题目中的式子就是 $(1 + \sum x_{i})^{2}$ ，wqs 二分 + 斜率优化。注意 wqs 二分的斜率可以达到 $- (1 + \sum x_{i})^{2}$ 即 $10^{16}$ 级别。

*XIII. P5633 最小度限制生成树

带权二分。视选择与 $s$ 相连的边为选择一个物品，将所有这样的边的权值减掉 $K$ 。无解的情况有：每次减去的权值 $K$ 最大时 $s$ 的度数大于 $k$ 或 $K$ 最小时 $s$ 的度数小于 $k$ 。

但若每次二分都对边重新排序，时间复杂度无法承受，可以一开始先进行初始化，则二分 check 内部只需要使用归并排序即可。时间复杂度 $O (m (\log m + \log V \log n))$ 。

注意本题有不使用带权二分的复杂度更优的神仙解法。见贪心专题。

*XIV. CF321E Ciel and Gondolas

看到这题笔者首先想到了 $O (k n \log n)$ 的决策单调性分治，代码。

猜测答案关于 $k$ 是上凸函数，故使用 wqs 二分 + 内层决策单调性二分队列将时间复杂度优化为 $O (n \log V \log n)$ 。代码。

*XV. 某模拟赛 AK 吧

$q$ 次询问在 $a_{l} \sim a_{r}$ 恰好选出 $k$ 段的最大子段和。 $n, q \leq 5 \times 10^{4}$ 。

关于最多选 $k$ 段的最大子段和有经典贪心做法，见 CF280D。但本题显然不可以 $n q \log n$ 做。

恰好选 $k$ 段让我们想到 wqs 二分。我们只需求出对于 $l \sim r$ ，如果每选一段就要付出 $K$ 的代价，最终选出几段以及对应的最大值。

区间询问考虑线段树，每个区间 $[l, r]$ 维护区间长度 $L$ 加 $1$ 条直线，分别表示选 $0, 1, 2, \dots L - 1, L$ 个段对应的代价。因为 固定段数，贡献随着斜率 $K$ 增大而 线性地 减小（因为每选一段就有 $K$ 的代价），因此，段数为 $k$ 的贡献表现出来的就是一条直线 $y = - k x + b$ 。 $b$ 表示恰好选 $k$ 段的最大子段和， $x$ 表示二分的斜率， $y$ 表示此时的贡献。

根据经典结论， $b_{k}$ 具有凸性，因此两个区间 $b_{p, i} = {max}_{j = 0}^{i} b_{l s, j} + b_{r s, i - j}$ 可直接类似闵可夫斯基和地贪心合并。并不需要显式地建出凸包，查询时在 $b$ 上二分即可得到该斜率（即横坐标）对应的段数（即直线斜率）。

由于子段的延伸情况仅和区间端点相关，故对每个区间分别记录两个端点总共四种状态。对于左端点为 $1$ 的状态，暂时不看作完整子段，当与左边的右端点为 $0$ 的区间合并时再计入，当与左边的右端点为 $1$ 的区间合并时可看做单独子段，也可以和左边区间最右子段合并。查询时也类似记录即可。

wqs 二分上下界为 $\sum a$ ，为了卡常可以适当调小一点。时间复杂度 $O (n \log^{2} n (\log n + \log a))$ 。

posted @ 2021-03-04 20:18 qAlex_Weiq 阅读(14172) 评论(16) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

阅读排行：
· 阿里最新开源QwQ-32B，效果媲美deepseek-r1满血版，部署成本又又又降低了！
· 单线程的Redis速度为什么快？
· SQL Server 2025 AI相关能力初探
· AI编程工具终极对决：字节Trae VS Cursor，谁才是开发者新宠？
· 展开说说关于C#中ORM框架的用法！

公告

昵称： qAlex_Weiq
园龄： 4年3个月
粉丝： 918
关注： 56

+加关注

2025年3月

日

一

二

三

四

五

六

qAlex_Weiq