《dp单调性优化》小结
\(wqs\) 二分 \((2D/1D)\)
王钦石二分又称带权二分,在国外又称 \(alien\ trick\) ,因为曾经考过一道叫 \(aliem\) 的题,用了这个方法。
而 \(2D\) 中一般来说第二维是选取物品个数。
算法介绍
这个算法能用当且仅当答案是 \(\color{red}\text{凸包}\) 时,我们才能使用。
假如我们有一个问题,给我们 \(n\) 个数,我们必须要选 \(k\) 个数,让我们求答案最优解,但是这时候直接 \(O(nk)\) 做是不行的,所以要考虑其他做法。
我们记 \(g_i\) 表示当选择 \(i\) 个数时的最优解是多少,这个 \(g\) 我们不知道他的具体数值,只知道他是一个凸包,仅此而已。
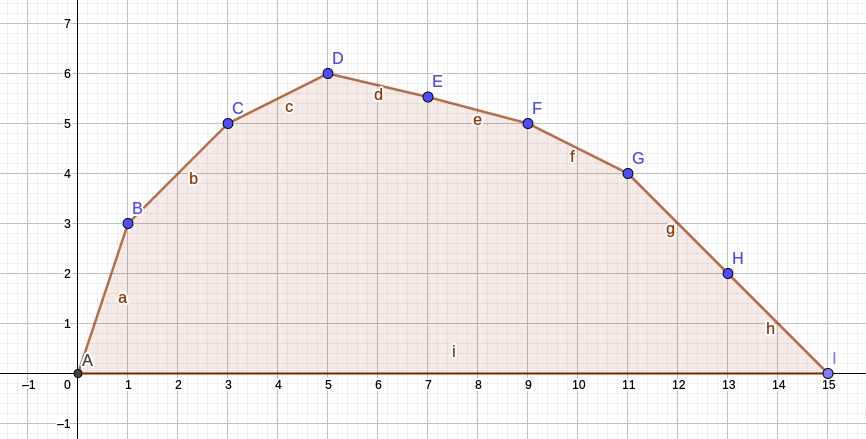
对于上图,我们记 \(x\) 轴为选了 \(x\) 个数, \(y\) 为选了 \(x\) 个数时的最优解是多少。
然后我们的目标是得到 \(g(m)\) 是多少。
我们先不考虑选取物品个数的限制,考虑二分一个斜率去切这个凸包。
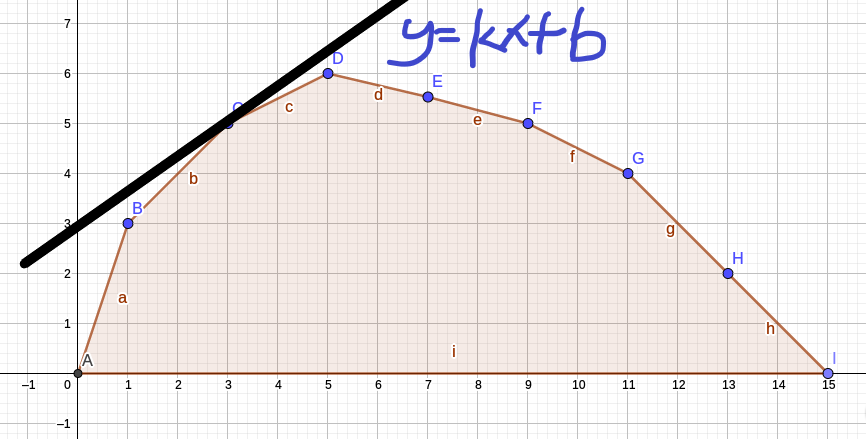
具体如何操作呢,每次我们都可以选数对吧,选完数之后我们额外给每次选数都加一笔手续费,就是说你每选一个数,就要减一次手续费,这个手续费就是我们二分的斜率这里记为 \(p\) (虽然图里画了 \(k\) ,但是懒得改了)
然后我们记录一下在每次操作减去这个手续费之后的最优解一共选取了多少个数,记为 \(ls\)。
然后倘若我们的 \(ls<m\) ,那么也就是说答案在我们的右边,我们需要把斜率变小,才有可能切到我们的答案(对于上图的上凸包而言是这样的,下凸包就要变大,不过真的有题目是下凸包吗?),而如果答案在左边同理。
那么我们就这样不断二分最终就可以切到答案。
我们的复杂度就从 \(O(nk)\) 降到了 \(O(n\log |V|)\)
- 解释一下为什么当手续费为斜率时,就可以切到对应的最优解,因为你最优解的增长本质上也是一个斜率,那么也就是说当最优解的增长小于我们的手续费时,你再取就不优了,所以我们的直线就可以切到斜率第一个小于他地方的最优解。
注意事项:
-
一般题目都为整数的时候,我们不需要二分实数斜率,否则会大幅度降低程序效率
-
三点共线 \(\color{red}\text{(敲黑板)}\)
这是初学者容易犯的错误,也是导致题目总是 \(WA\) 几个点的原因。

假设这四个点共线,那么如果我们用一条等于他们的斜率去切,那么我们切出来的是哪个点呢?
一般情况下,我们要钦定我们切的是相同价值下,选了 \(\text{最少/最多}\) 的是多少个数。
假如我们钦定选的是最少的。
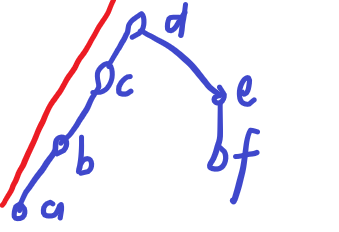
看 \(a,b,c,d\) 这四个点,假如这四个点三点共线,那么我们切出来的就是 \(a\) ,当我们的 \(m=c\) 时,怎么办呢。也就是说当 \(ls\le m\) 时,这个切出来的东西是有可能是答案的,那么我们就要把答案带进去计算一下贡献,不过我们要注意一下答案是 \(g_a+mid\times m\) 而不是 \(g_a+mid\times a\) ,因为我们要的答案是 \(g_c\) ,虽然如果减去手续费我们的答案是不变的,不过最终我们要的答案是 \(g(c)\) ,在不减去手续费的时候是有增益的。而 \(le>m\) ,那么就一定不可能成为答案,一般长这样。
实战中一般把最优解和选的数的个数绑起来,丢到一个结构体里面,重载一下大于小于号,这样方便一点。
实战演练:
一般在实战中我们都是猜答案是凸的,很难去证明,可以打表找规律。当然也可以大胆猜测:
nk做不了就是凸的
以下讲解都不证明答案的凸性。
P2619 [国家集训队] Tree I
先将黑边和白边分一个类,两种类内部排好序。
然后二分一个斜率 \(mid\)
然后用类似于归并排序,对于白边如果 \(-mid\) 之后,仍比黑边大就选它。
然后差不多就做完了,要注意斜率可以取负数。
时间复杂度 \(O(n\log |V|)\)
点击查看代码
#include<bits/stdc++.h>
typedef long long LL;
using namespace std;
const int MAXN=1e5+10;
int n,m,k,cnt1,cnt2;
struct daduoli {
int f,t,c;
}a[MAXN],b[MAXN];
int fa[MAXN],kk,cost;
int find(int x) {
return (fa[x]==x?x:fa[x]=find(fa[x]));
}
int res;
void add(int f,int t,int c,int col) {
int xx=find(f),yy=find(t);
// if(res) cout<<xx<<' '<<yy<<endl;
if(xx==yy) return ;
cost+=c;
fa[xx]=yy; kk+=(!col);
}
void calc(int x) {
for(int i=1;i<=n;++i) fa[i]=i;
int l1=1,l2=1;
kk=0; cost=0;
while(l1<=cnt1&&l2<=cnt2) {
if(a[l1].c-x<=b[l2].c) {
add(a[l1].f,a[l1].t,a[l1].c-x,0);
++l1;
}
else {
add(b[l2].f,b[l2].t,b[l2].c,1);
++l2;
}
}
while(l1<=cnt1) add(a[l1].f,a[l1].t,a[l1].c-x,0),++l1;
while(l2<=cnt2) add(b[l2].f,b[l2].t,b[l2].c,1),++l2;
}
int erfind() {
int l=-101,r=101,mid;
while(l+1<r) {
mid=(l+r)/2;
calc(mid);
if(kk<k) l=mid;
else r=mid;
}
return r;
}
bool cmp(daduoli a,daduoli b) {
return a.c<b.c;
}
int main () {
scanf("%d%d%d",&n,&m,&k);
for(int i=1;i<=m;++i) {
int f,t,c,col;
scanf("%d%d%d%d",&f,&t,&c,&col);
++f; ++t;
if(!col) {
a[++cnt1]=(daduoli){f,t,c};
}
else {
b[++cnt2]=(daduoli){f,t,c};
}
}
sort(a+1,a+1+cnt1,cmp);
sort(b+1,b+1+cnt2,cmp);
int p=erfind();
calc(p);
printf("%d\n",cost+p*k);
return 0;
}
P5633 最小度限制生成树
\(GDKOI2023\) 原题
这题和上一题很像,把和 \(s\) 有关的边与不是 \(s\) 有关的边分一类,然后去跑即可。
不过这题对于判断 \(Impossible\) 的情况有点刁钻。
有一种比较好的方法:
-
首先如果和 \(s\) 有关的边不足 \(k\) 条肯定可以直接判掉。
-
然后我们先把与 \(s\) 无关的全部连起来,然后再去连与 \(s\) 有关的边,如果需要的边大于 \(k\) ,那么也可以判掉。
这样做的正确性可以证明,但我不会。
点击查看代码
#include<bits/stdc++.h>
typedef long long LL;
using namespace std;
const int MAXN=5e5+10;
int n,m,k,cnt1,cnt2,s;
struct daduoli {
int f,t,c;
}a[MAXN],b[MAXN];
int fa[MAXN],kk,cost;
int find(int x) {
return (fa[x]==x?x:fa[x]=find(fa[x]));
}
int res,kkk;
void add(int f,int t,int c,int col) {
int xx=find(f),yy=find(t);
if(xx==yy) return ;
cost+=c;
fa[xx]=yy; kk+=(!col); ++kkk;
}
bool vis[MAXN];
int ttt;
void calc(int x) {
for(int i=1;i<=n;++i) fa[i]=i;
int l1=1,l2=1;
kk=0; cost=0; kkk=0;
while(l1<=cnt1&&l2<=cnt2) {
if(a[l1].c-x<=b[l2].c) {
add(a[l1].f,a[l1].t,a[l1].c-x,0);
++l1;
}
else {
add(b[l2].f,b[l2].t,b[l2].c,1);
++l2;
}
}
while(l1<=cnt1) add(a[l1].f,a[l1].t,a[l1].c-x,0),++l1;
while(l2<=cnt2) add(b[l2].f,b[l2].t,b[l2].c,1),++l2;
}
int erfind() {
int l=-30001,r=30001,mid;
while(l+1<r) {
mid=(l+r)/2;
calc(mid);
if(kk<k) l=mid;
else r=mid;
}
return r;
}
bool cmp(daduoli a,daduoli b) {
return a.c<b.c;
}
int main () {
scanf("%d%d%d%d",&n,&m,&s,&k);
for(int i=1;i<=m;++i) {
int f,t,c;
scanf("%d%d%d",&f,&t,&c);
if(f==s||t==s) {
a[++cnt1]=(daduoli){f,t,c};
}
else {
b[++cnt2]=(daduoli){f,t,c};
}
}
if(cnt1<k) {
puts("Impossible");
return 0;
}
for(int i=1;i<=n;++i) fa[i]=i;
for(int i=1;i<=cnt2;++i) {
add(b[i].f,b[i].t,0,1);
}
for(int i=1;i<=cnt1;++i) {
add(a[i].f,a[i].t,0,0);
}
if(kk>k) {
puts("Impossible");
return 0;
}
for(int i=1;i<=n;++i) {
fa[i]=find(fa[i]);
if(!vis[fa[i]]) {
++ttt;
vis[fa[i]]=1;
}
}
if(ttt>1) {
puts("Impossible");
return 0;
}
sort(a+1,a+1+cnt1,cmp);
sort(b+1,b+1+cnt2,cmp);
int p=erfind();
calc(p);
printf("%d\n",cost+p*k);
return 0;
}
P1484 种树
首先我们要求的是种至多 \(k\) 棵树的最优解,而不是种恰好 \(k\) 棵树的最优解。
这怎么办呢,因为答案是凸的,我们找到峰值,如果峰值在 \(0\sim k\) 中,那么直接输出峰就好了。
否则他就是一段单调上升的区间,在 \(k\) 内。
然后我们去 \(wqs\) 二分就好了,不过要注意要钦定选最少或最多,不然你是过不去的,就是要加第二维,表示选了多少个数。
点击查看代码
#include<bits/stdc++.h>
typedef long long LL;
using namespace std;
const LL MAXN=5e5+10;
LL n,k;
LL A[MAXN];
LL res,ans,anss;
LL calc(LL mid) {
LL l1=0,x=0,l2=0,xx=0;
for(int i=1;i<=n;++i) {
LL a=l1,aa=x,b=l2,bb=xx;
if(b>l1||(b==l1&&bb<=x)) {
l1=b;
x=bb;
}
l2=a+(A[i]+mid);
xx=aa+1;
}
ans=max(l1,l2);
if(l1==l2) return min(x,xx);
if(l1>l2) return x;
return xx;
}
LL erfind() {
LL l=-1e6-1,r=1e6+1,mid;
while(l+1<r) {
mid=(l+r)/2;
LL ls=calc(mid);
if(ls<=k) {
l=mid;
anss=ans-mid*k;
}
else r=mid;
}
return l;
}
int main () {
scanf("%lld%lld",&n,&k);
for(int i=1;i<=n;++i) {
scanf("%lld",&A[i]);
}
LL p;
p=erfind();
printf("%lld\n",anss);
return 0;
}
Gosha is hunting
首先明显直接暴力做是肯定要三维的,优化不了。
大胆猜测一波凸性。
然后我们可以优化掉第二维,然后就做完了,时间复杂度 \(O(n^2\log |V|)\)
P4072 [SDOI2016] 征途
原本斜优和 \(wqs\) 二分里面选一个就直接可以做掉了,不过如果你两个都用就可以获得 \(O(n\log |V|)\) 的优秀时间复杂度,跑进最优解第一页
点击查看代码
#include<bits/stdc++.h>
typedef long long LL;
using namespace std;
const int MAXN=3010,inf=1e15+10;
int n,m;
int a[MAXN],s[MAXN],y[MAXN];
int que[MAXN];
double T(int i,int j) {
if(s[i]==s[j]) return -inf;
return (y[i]-y[j])*1.0/(1.0*s[i]-s[j]);
}
struct daduoli {
int f,c;
friend bool operator <(daduoli a,daduoli b) {
return (a.f<b.f||(a.f==b.f&&a.c<b.c));
}
}f[MAXN];
int ans,anss;
int calc(int x) {
f[0].f=0; f[0].c=0; y[0]=-x;
int head=1,tail=0;
for(int j=1;j<=n;++j) {
f[j].f=inf; f[j].c=inf;
if(f[j-1].f<inf) {
while(head<tail&&T(que[tail-1],que[tail])>T(que[tail],j-1)) --tail;
que[++tail]=j-1;
}
while(head<tail&&T(que[head],que[head+1])<2*s[j]*m) ++head;
if(head<=tail) {
f[j].f=(y[que[head]]-2*s[j]*s[que[head]]*m+s[j]*s[j]*m);
f[j].c=f[que[head]].c+1;
y[j]=f[j].f+s[j]*s[j]*m-x;
}
}
ans=f[n].f-s[n]*s[n];
return f[n].c;
}
void erfind() {
int l=-1e9,r=0,mid;
while(l+1<r) {
mid=(l+r)/2;
int ls=calc(mid);
if(ls<=m) {
l=mid;
anss=ans+m*mid;
}
else r=mid;
}
}
int main () {
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i) {
scanf("%d",&a[i]);
s[i]=s[i-1]+a[i];
}
erfind();
printf("%d\n",anss);
return 0;
}
P4983 忘情
这题就是上一题的加强版,强制你两个都要用。
点击查看代码
#include<bits/stdc++.h>
typedef long long LL;
using namespace std;
const LL MAXN=1e5+10,inf=1e15+10;
LL n,m;
LL a[MAXN],s[MAXN],y[MAXN];
LL que[MAXN];
double T(LL i,LL j) {
if(s[i]==s[j]) return -inf;
return (y[i]-y[j])*1.0/(1.0*s[i]-s[j]);
}
struct daduoli {
LL f,c;
friend bool operator <(daduoli a,daduoli b) {
return (a.f<b.f||(a.f==b.f&&a.c<b.c));
}
}f[MAXN];
LL ans,anss;
LL calc(LL x) {
f[0].f=0; f[0].c=0; y[0]=-x+1;
int head=1,tail=0;
for(int j=1;j<=n;++j) {
f[j].f=inf; f[j].c=inf;
if(f[j-1].f<inf) {
while(head<tail&&T(que[tail-1],que[tail])>T(que[tail],j-1)) --tail;
que[++tail]=j-1;
}
while(head<tail&&T(que[head],que[head+1])<2*s[j]) ++head;
if(head<=tail) {
int t=que[head];
f[j].f=(y[t]-2*s[j]*s[t]+s[j]*s[j]+2*s[j]);
f[j].c=f[t].c+1;
y[j]=f[j].f+s[j]*s[j]-2*s[j]+1-x;
}
}
ans=f[n].f;
return f[n].c;
}
void erfind() {
LL l=-1e18,r=0,mid;
while(l+1<r) {
mid=(l+r)/2;
int ls=calc(mid);
if(ls<=m) {
l=mid;
anss=ans+m*mid;
}
else r=mid;
}
}
int main () {
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;++i) {
scanf("%lld",&a[i]);
s[i]=s[i-1]+a[i];
}
erfind();
printf("%lld\n",anss);
return 0;
}
P4383 [八省联考 2018] 林克卡特树
唯一一道不是那么模板的题。
题意就是让你将树分成若干个连通块使得每个连通块的直径之和最大。
首先考虑如何设计状态 \(f_{i,j,0/1/2}\) 表示以 \(i\) 为根的子树中分了 \(j\) 个连通块,然后当前点度数为 \(0/1/2\) (注意先不考虑与父节点直接的连边)
当度数为 \(0\) ,就是一个孤立点。
当度数为 \(1\) 时,就是一条链。
当对数为 \(2\) 时长这样,延伸到 \(u\) 的某两个子树中:
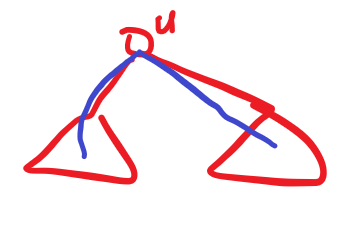
考虑转移
\(dp_{i,j,0}=\max (dp_{i,q,0}+dp_{t,j-q,0})\)
\(dp_{i,j,1}=\max (dp_{i,q,0}+dp_{t,j-q,1}+val,dp_{i,q,1}+dp_{t,j-q,0})\)
\(dp_{i,j,2}=\max (dp_{i,q,1}+dp_{t,j-q,1}+val,dp_{i,q,2}+dp_{t,j-q,0})\)
那么上面的这三个转移也是比较显然了。
然后是更新独立成为一个新的连通块,这些也不细说,细节我都忘得差不多了。。。
过了 \(15\) 天才会来写这个东西。
暴力代码长这样:
点击查看代码
#include<bits/stdc++.h>
typedef long long LL;
using namespace std;
const int MAXN=3e5+10;
const LL inf=-1e18;
int n,k;
struct ddl {
int t,c;
};
vector<ddl> e[MAXN];
void add(int f,int t,int c) {
e[f].push_back((ddl){t,c});
e[t].push_back((ddl){f,c});
}
LL f[3][MAXN][110];
void dfs(int u,int fa) {
for(int i=0;i<=k;++i) {
f[0][u][i]=f[1][u][i]=f[2][u][i]=inf;
}
f[0][u][0]=0; f[1][u][0]=0; f[2][u][0]=0;
for(auto t:e[u]) {
if(t.t==fa) continue;
dfs(t.t,u);
int z=t.t;
for(int j=k;j>=0;--j) {
for(int q=0;q<=j;++q) {
int y=j-q;
if(q)
f[2][u][j]=max(f[2][u][j],max(f[1][u][y]+f[1][z][q-1]+t.c,f[2][u][y]+f[0][z][q]));
else
f[2][u][j]=max(f[2][u][j],f[2][u][y]+f[0][z][q]);
f[1][u][j]=max(f[1][u][j],max(f[0][u][y]+f[1][z][q]+t.c,f[1][u][y]+f[0][z][q]));
f[0][u][j]=max(f[0][u][j],f[0][u][y]+f[0][z][q]);
}
}
}
for(int i=1;i<=k;++i) f[0][u][i]=max(f[0][u][i],max(f[1][u][i-1],f[2][u][i]));
}
int main () {
scanf("%d%d",&n,&k);
for(int i=1;i<n;++i) {
int x,y,c;
scanf("%d%d%d",&x,&y,&c);
add(x,y,c);
}
++k; dfs(1,0);
printf("%lld\n",f[0][1][k]);
return 0;
}
然后如果考场上你人类智慧发现了凸性,你就套上 \(wqs\) 二分,通过此题。
点击查看代码
#include<bits/stdc++.h>
typedef long long LL;
using namespace std;
const int MAXN=3e5+10;
const LL inf=-1e18;
int n,k;
struct ddl {
int t,c;
};
vector<ddl> e[MAXN];
void add(int f,int t,int c) {
e[f].push_back((ddl){t,c});
e[t].push_back((ddl){f,c});
}
struct daduoli {
LL x,c;
friend bool operator <(daduoli a,daduoli b) {
return (a.x<b.x||(a.x==b.x&&a.c>b.c));
}
friend daduoli operator +(daduoli a,daduoli b) {
return (daduoli){a.x+b.x,a.c+b.c};
}
void init() {
x=-inf;
c=0;
}
}f[3][MAXN];
daduoli tr[3],lsls;
LL ans,anss;
void dfs(int u,int fa,LL x) {
f[2][u]=max(f[2][u],lsls);
for(auto t:e[u]) {
if(t.t==fa) continue;
int z=t.t;
daduoli pp;
pp.c=0; pp.x=t.c;
dfs(z,u,x);
for(int j=0;j<3;++j) tr[j].init();
tr[0]=f[0][u]+f[0][z];
tr[1]=max(f[1][u]+f[0][z],f[0][u]+f[1][z]+pp);
tr[2]=max(f[2][u]+f[0][z],f[1][u]+f[1][z]+lsls+pp);
for(int j=0;j<3;++j) f[j][u]=tr[j];
}
f[0][u]=max(f[0][u],max(f[1][u]+lsls,f[2][u]));
}
int calc(LL x) {
memset(f,0,sizeof(f));
lsls.c=1; lsls.x=-x;
dfs(1,0,x);
ans=f[0][1].x;
return f[0][1].c;
}
void erfind() {
LL l=-1e11,r=1e11,mid;
while(l+1<r) {
mid=(l+r)/2;
int ls=calc(mid);
if(ls<=k) {
r=mid;
anss=ans+k*mid;
}
else l=mid;
}
return ;
}
int main () {
scanf("%d%d",&n,&k);
for(int i=1;i<n;++i) {
int x,y,c;
scanf("%d%d%d",&x,&y,&c);
add(x,y,c);
}
++k;
erfind();
printf("%lld\n",anss);
return 0;
}
总结:
其实可以发现很多时候,就是暴力写出状态,然后你猜一下答案是否有凸性,如果你猜得到,你就直接套上板子,做出来了,实际上这更多的是一种优化的工具,一般写题重点都不在 \(wqs\) 二分。
不过考场上如果想证凸性是比较困难的,最实用的方法就是打表!!!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号