《LGJOJ 9.10》测试总结

今天又是被打爆的一天，没什么好说的了。

\(T1\) 二次在线可持久化动态 \(trie\) 树分治维护全局动态仙人掌连通性

我是 \(sb\) ，写了一个多小时，才写出来。

首先我们考虑暴力，直接 \(n^2\) 做。

然后考虑正解怎么做，首先对 \(a\) 建一棵 \(trie\) 树，然后再在每个 \(a\) 的节点上建一个 \(b\) 的 \(trie\) 树，但这样是不行的，因为我们还是得遍历 \(a\) 的整颗 \(trie\) 树。

我们思考为什么刚才做不了，因为我们把 \(a,b\) 两个信息给拆开来了，通过刚才失败的教训，我们可以发现，必须要建出一个与 \(a,b\) 都有关的 \(trie\) 树，我们才有可能得到一个正确的算法。

但是因为 \(\oplus\) 比较特殊，你如果把他 \(+,\times,-,/\)

都不太可以做，我们考虑把 \(a\oplus b\) 丢到 \(trie\) 树上。

然后我们查询的时候也是用 \(x\oplus y\) 进行查询。

当我们遇到 \(x\oplus y=0\) 的时候，有两种情况。

\((x=0,y=0),(x=1,y=1)\) 我们这时候 假设前面的 \(x\oplus a,y\oplus b\) 全部都相同，那么这时候 \(a,b\) 有四种情况。

\((a=0,b=0),(a=0,b=1),(a=1,b=0),(a=1,b=1)\)

我们发现当 \((a=0,b=0),(a=1,b=1)\) 异或上 \(x,y\) 不管是那种情况，仍然相同，而 \((a=0,b=1),(a=1,b=0)\) 异或上 \(x,y\) 不管是那种情况，都是一定有一个会大于另一个，所以我们只需要遍历 \(a^b=0\) 的情况就可以了，然后对于 \(a^b=1\) 的情况，根据 \(x,y\) 的情况，讨论一下，算一下贡献就行了。

而对于 \(x\oplus y=1\) 的情况也是同理即可。

时间复杂度 \(O(m\log |V|)\)

点击查看代码

#include<bits/stdc++.h>
typedef long long LL;

using namespace std;
const int MAXN=2e5+10,NN=1.5e7+10;
LL n;
LL x,y,opt,tot;
int tr[NN][2];
int a1[NN],a2[NN];
struct daduoli {
	LL x,y;
}a[MAXN];
void insert(LL x,int val,LL p) {
	int u=0;
	for(int i=63;i>=0;--i) {
		int t=((x>>i)&1);
		if(!tr[u][t]) tr[u][t]=++tot;
		u=tr[u][t];
		if(!((p>>i)&1)) a1[u]+=val;
		else a2[u]+=val;
	}
}
int query(LL x,LL p) {
	LL ans=0,sf=0;
	int u=0;
	for(int i=63;i>=0;--i) {
		int t=((x>>i)&1),ls;
		if(tr[u][t^1]) {
			ls=tr[u][t^1];
			if(((p>>i)&1)) ans+=a1[ls];
			else ans+=a2[ls];
		}
		if(tr[u][t]) u=tr[u][t];
		else break;
	}
	return ans;
}
int main () {
	scanf("%lld",&n);
	for(int i=1;i<=n;++i) {
		scanf("%lld%lld%lld",&opt,&x,&y);
		if(opt==1) {
			insert((x^y),1,x);
		}
		if(opt==2) {
			insert((x^y),-1,x);
		}
		if(opt==3) {
			printf("%d\n",query((x^y),x));
		}
	}
	return 0;
}
/*
6
3 1 2
1 3 2
1 4 5
3 6 2
2 3 2
3 6 2
*/

\(T2\) 最棒的玩具销售员

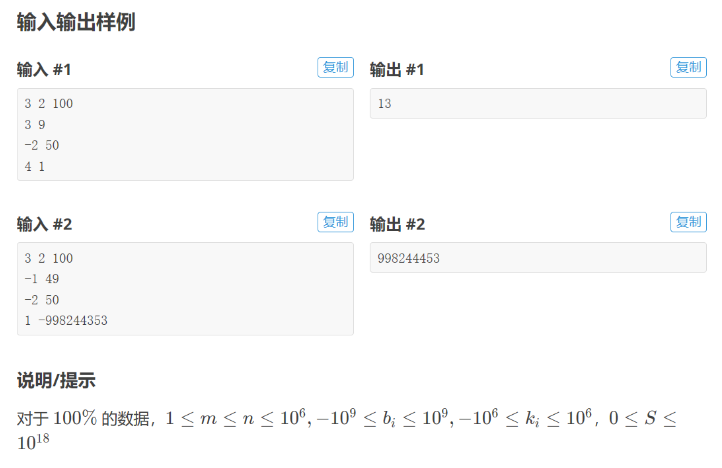
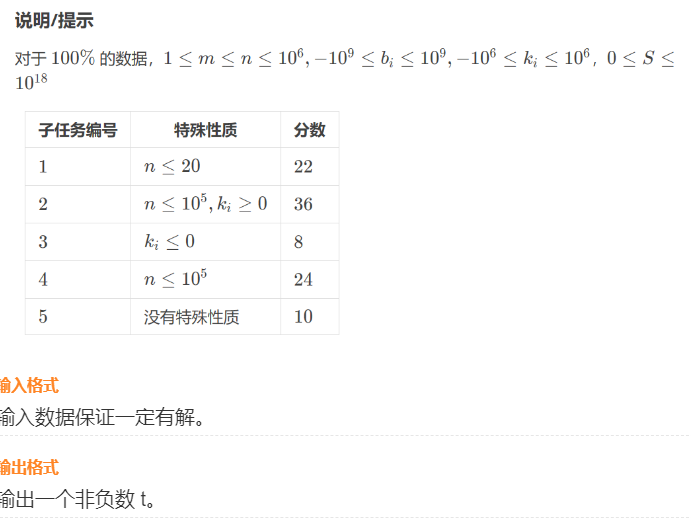
首先我们答案关于时间的函数长这样。

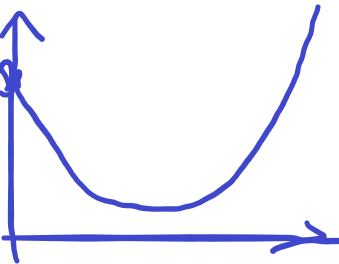
是一个下凸包。

这个东西看上去就让人很像二分，但是他并没有单调性。

我们观察可以发现，对于斜率为负数的，他只有可能在 \(0\) 时刻取到，否则就一定不优。

所以说我们先在 \(0\) 时刻，判掉取负数的情况，然后就如下图。

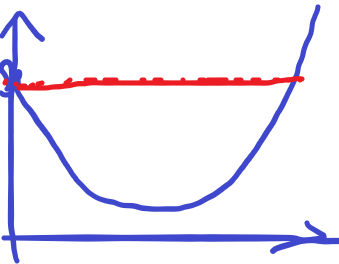
我们可以把红线下面这段的 \(ans\) 全部给移成这条红线，这样我们的函数就有单调性了。

所以我们就可以二分了，但是由于我们需要排序，所以时间复杂度是 \(O(n\log^2 n)\)

可以用 \(nth\_element\) 在 \(O(n)\) 的时间内找到第 \(k\) 大的值，然后把大于等于这个数的值全部加起来，再判断即可。（不过如果存在相同的数，需要另外判断，不过我的代码里没有判，但是数据水，没有卡掉我）

时间复杂度 \(O(n\log n)\)

中间运算用一下 \(\_\_int128\) 最好，怕爆 \(long\ long\)

点击查看代码

#include<bits/stdc++.h>
#pragma GCC optimize(3,"Ofast","inline")
typedef long long LL;

using namespace std;
inline LL read(){
    LL x=0,f=1;
    char ch=getchar();
    while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
    while(isdigit(ch)){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
    return x*f;
}
inline void write(__int128 x){
    if(x<0){
        putchar('-');
        x=-x;
    }
    if(x>9)
        write(x/10);
    putchar(x%10+'0');
}

const __int128 MAXN=1e6+10;
__int128 n,m,S,T;
__int128 b[MAXN];
struct daduoli {
	__int128 k,b;
}a[MAXN];
bool cmp(daduoli a,daduoli b) {
	return a.b>b.b;
}
bool check(__int128 x) {
	int cnt=0;
	for(int i=1;i<=n;++i) {
		b[i]=a[i].k*x+a[i].b;
		if(b[i]>0) b[++cnt]=b[i];
	}
	int l=cnt-m+1;
	if(l<1) l=1;
	nth_element(b,b+l,b+1+cnt);
	__int128 ls=0;
	for(int i=1;i<=cnt;++i) {
		if(b[i]>=b[l]) {
			ls+=b[i];
		}
		if(ls>=S) return true;
	}
	return false;
}
__int128 erfind() {
	__int128 l=0,r=1e18+1,mid;
	while(l+1<r) {
		mid=(l+r)/2;
		if(check(mid)) r=mid;
		else l=mid;
	}
	return r;
}
int main () {
	n=read(); m=read(); S=read();
	for(int i=1;i<=n;++i) {
		a[i].k=read(); a[i].b=read();
	}
	sort(a+1,a+1+n,cmp);
	__int128 ls=0;
	for(int i=1;i<=m;++i) {
		if(a[i].b<=0) break;
		ls+=a[i].b;
	}
	if(ls>=S) {
		puts("0");
		return 0;
	}
	write(erfind());
	return 0;
}
/*
3 2 100
3 9
-2 50
4 1

3 2 100
-1 49
-1 50
2 1 
*/

\(T3\) 喵了个喵Ⅳ

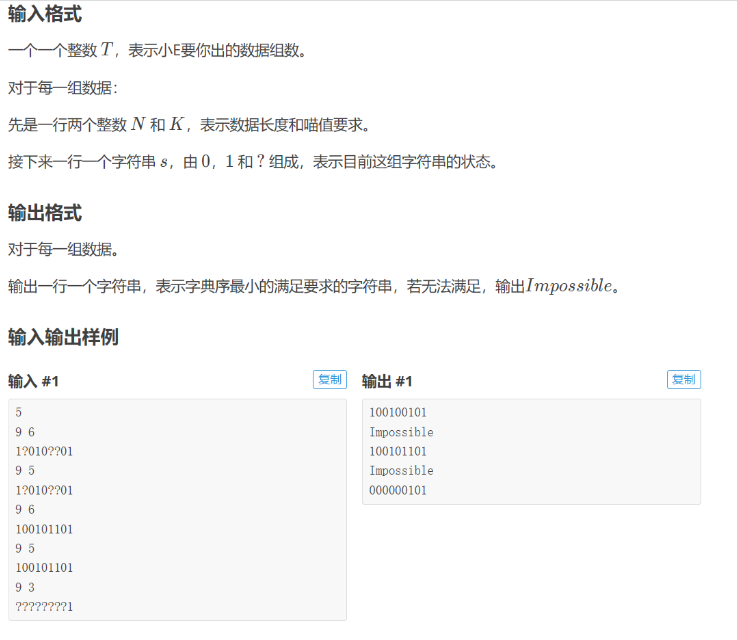
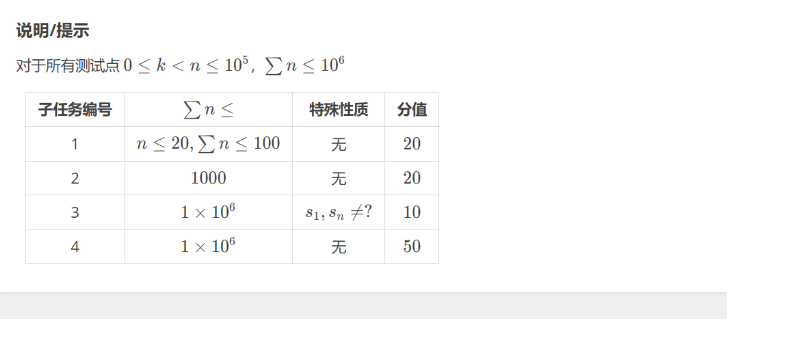
好题。

主流有三种方法。

我们先考虑暴力直接 \(O(nk)\) 即可，但是不知道为什么我暴力都写挂了，很奇怪。

第一种方法：

优化暴力，不找出所有情况，只考虑可能成为最优解的。我们考虑贪心，我们肯定是想前面取的越小越好，我们采用试填法，将 \(0\) 填进去，看一下后面能不能顺着这个构造出对应方案。

如果不行，就试 \(1\) ，如果还是不行，就 \(Impossible\)

那么现在的问题就变成了如何快速判断后面能否填出一段瞄值为 \(p\) 的序列， \(p\) 是一个常数。

快速判断的话，可以求出可能的上下界，然后只要 \(p\) 在这个上下界之间，那就一定可以构造出来，不过前提是同奇偶，所以对于奇数偶数都要算一下。

第二种方法：

先把全部的 \(?\) 都填成 \(0\) ，然后记此时的瞄值为 \(m\) 。

如果我们调整一个 \(?\) ，那么我们的瞄值的变化量是 \(+2,0,-2\) 中的其中一个。

所以如果 \(m\) 和 \(k\) 的奇偶性不同，那么我们是无解的。

如果 \(m<k\) 那么就从后往前把一些 \(0\) 改成 \(1\)

如果 \(m>k\) 那么就把一些左右两边为 \(1\) 的段改成全部改成 \(1\) 即可。

第三种方法：

这是我觉得比较好写，而且思路比较清晰的一种方法，来自 \(hpz\) 大神， \(orz\)

考虑我们 \(?\) 分成一段一段，那么有四种情况。

• 这一段问号的左边是 \(0\) ，右边也是 \(0\)

• 左边是 \(0\) ，右边是 \(1\)

• 左边是 \(1\) ，右边是 \(0\)

• 左边是 \(1\) ，右边是 \(1\)

有四种情况，你如果直接处理起来，是比较困难的。

\(\color{red}\text{考虑化异为同，化繁为简。}\)

我们先考虑只有左右两边都是 \(0\) 的区间的时候如何算贡献，从后往前枚举这些区间， \(010101....\) 这样间隔填即可。所以我们填的 \(1\) 的数量越少越好，也就是我们需要贡献的瞄值越少越好。

先对左边是 \(1\) ，右边是 \(0\) ，和左边是 \(0\) ，右边是 \(1\) 的情况进行讨论。

我们可以在 \(1\) 的旁边填上一个 \(0\) ，转化成左右两边都是 \(1\) 的，因为我们这样的区间，他对瞄值的贡献一定至少是 \(1\) ，而如果我们填上一个 \(0\) 之后，实际上我们相当于把这一个贡献提前计算，而且一定不可能有比这个还有优的，因为 \(0\) 是最小值。

考虑左边是 \(1\) ，右边也是 \(1\) 的情况，如果此时瞄值 \(+2<k\) ，那么我们就在这两个 \(1\) 的旁边都填上 \(0\) ，因为否则就要全填 \(1\) 这肯定是不优的，而且我们还可以贡献两点瞄值，根据上面我们需要的瞄值越少越好而言，我们这样是优的。

这样，我们全部区间都转化成了左右两边都是 \(0\) 的区间。

然后从后往前填这些区间就可以了。

\(T4\) 罗必达法则

看这个